简述

论文地址：https://arxiv.org/abs/1506.02025

2015NIPS论文

Google DeepMind 出品的论文（alpha 狗就是他家的），STN（Spatial Transformer Network）网络可以作为一个模块嵌入任何的网络，它有助于选择目标合适的区域并进行尺度变换，可以简化分类的流程并且提升分类的精度。

CNN 虽然具有一定的不变性，如平移不变性，但是其可能不具备某些不变性，比如：缩放不变性、旋转不变性。某些 CNN 网络学会对不同尺度的图像进行识别，那是因为训练的图像中就包含了不同尺度的图像，而不是CNN具有缩放不变性。

研究者认为，既然某些网络可能隐式的方式学会了某些变换，如缩放、平移等，那为什么不直接通过显式的方式让网络学会变换呢？所以学者们提出了 STN 网络来帮助网络学会对图像进行变换，帮助提升网络的性能。

空间变换知识

该论文主要涉及三种变换，分别是仿射变换、投影变换、薄板样条变换（Thin Plate Spline Transform）。

仿射变换

仿射变换，又称仿射映射，是指在几何中，对一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。

变换的公式是

卷积神经网络之-STN(空间注意力机制） - 图1

变换的方式包括 Translate（平移）、Scale（缩放）、Rotate（旋转）、Shear（裁剪）等方式，将公式中的矩阵 A 和向量 b 更换成下面的数，就可以进行对应方式的变换。

image.png

投影变换

投影变换是仿射变换的一系列组合，但是还有投影的扭曲，投影变换有几个属性：1) 原点不一定要映射到原点 2) 直线变换后仍然是直线，但是一定是平行的 3) 变换的比例不一定要一致。

image.png

薄板样条变换 (TPS)

薄板样条函数 (TPS) 是一种很常见的插值方法。因为它一般都是基于 2D 插值，所以经常用在在图像配准中。在两张图像中找出 N 个匹配点，应用 TPS 可以将这 N 个点形变到对应位置，同时给出了整个空间的形变 (插值)。

1_ZSbO6OsydMhQxsRpIaWdXQ.png

STN 网络

STN 网络模型如下所示，包含三个部分：定位网络（Localisation network）、网格生成器（Grid generator）、采样器（Sampler）。
image.png

Localisation network

Localisation network 用来生成仿射变换的系数，输入 U(可以是图片，也可以是特征图)是 C 通道，高 H，宽 W 的数据，输出是一个空间变换的系数 卷积神经网络之-STN(空间注意力机制） - 图6，卷积神经网络之-STN(空间注意力机制） - 图7 的维度大小根据变换类型而定，如果是仿射变换，则是一个 6 维的向量。

Grid generator

网格生成器，就是根据上面生成的 卷积神经网络之-STN(空间注意力机制） - 图8 参数，对输入进行变换，这样得到的就是原始图像或者特征图经过平移、旋转等变换的结果，转换公式如下：

image.png

Sampler

根据 Grid generator 得到的结果，从中生成一个新的输出图片或者特征图 V，用于下一步操作

image.png

实验结果

MNIST

image.png
不同模型，使用不同变换下 MNIST 数据的测试误差

注意：上面的 FCN 指的是没有卷积的全连接网络，而不是全卷积网络

从上面可以看出：ST-FCN 优于 FCN，ST-CNN 优于 CNN；ST-CNN 始终优于 ST-FCN。

1_P_nv_a_Q3LqM9d10XGE3TQ.gif

SVHN（街景门牌号）

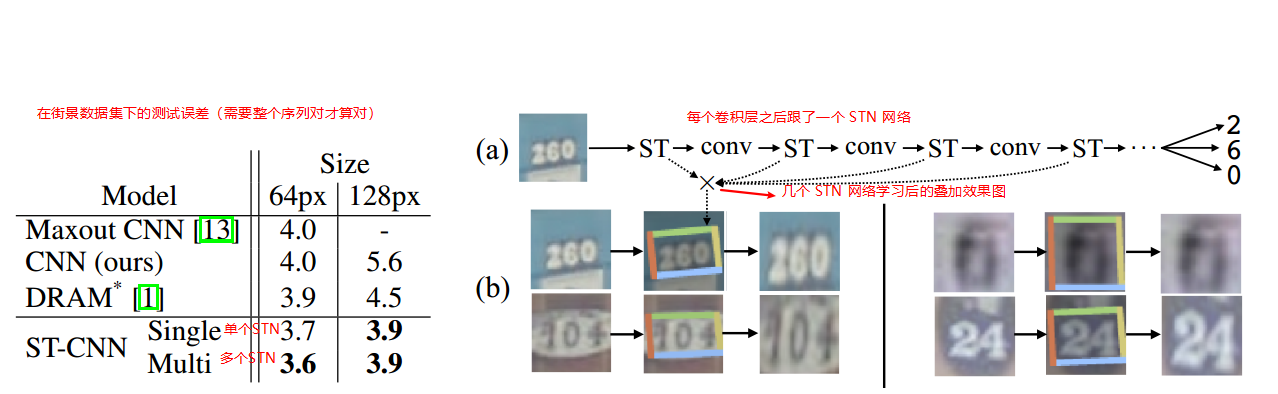
image.png

细粒度分类数据集（CUB-200-2011）

在细粒度数据集中，作者在网络中并行使用了多个 STN 网络，如下图，使用的是 2 个 STN 网络并行
image.png

image.png
在 CUB-200-2011 鸟类数据集上的测试精度

可以看出，使用多个 STN 并行的网络，可以使精度达到不错的效果，4 个 STN 并行的网络效果更好。


实现代码

  1. # 针对 MNIST 数据集（1×28×28 大小）设计的 STN 网络
  2. class Net(nn.Module):
  3.     def __init__(self):
  4.         super(Net, self).__init__()
  5.         self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
  6.         self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
  7.         self.conv2_drop = nn.Dropout2d()
  8.         self.fc1 = nn.Linear(320, 50)
  9.         self.fc2 = nn.Linear(50, 10)
  11.         # Spatial transformer localization-network
  12.         self.localization = nn.Sequential(
  13.             nn.Conv2d(1, 8, kernel_size=7),
  14.             nn.MaxPool2d(2, stride=2),
  15.             nn.ReLU(True),
  16.             nn.Conv2d(8, 10, kernel_size=5),
  17.             nn.MaxPool2d(2, stride=2),
  18.             nn.ReLU(True)
  19.         )
  21.         # Regressor for the 3 * 2 affine matrix
  22.         # 3 * 2 仿射矩阵 (affine matrix) 的回归器
  23.         self.fc_loc = nn.Sequential(
  24.             nn.Linear(10 * 3 * 3, 32),
  25.             nn.ReLU(True),
  26.             nn.Linear(32, 3 * 2)
  27.         )
  29.         # Initialize the weights/bias with identity transformation
  30.         # 初始化仿射系数的权重
  31.         self.fc_loc[2].weight.data.zero_()
  32.         self.fc_loc[2].bias.data.copy_(torch.tensor([1, 0, 0, 0, 1, 0], dtype=torch.float))
  34.     # Spatial transformer network forward function
  35.     def stn(self, x):
  36.         xs = self.localization(x)
  37.         xs = xs.view(-1, 10 * 3 * 3)
  38.         theta = self.fc_loc(xs)
  39.         theta = theta.view(-1, 2, 3)
  41.         grid = F.affine_grid(theta, x.size())
  42.         x = F.grid_sample(x, grid)
  44.         return x
  46.     def forward(self, x):
  47.         # transform the input
  48.         x = self.stn(x)
  50.         # Perform the usual forward pass
  51.         x = F.relu(F.max_pool2d(self.conv1(x), 2))
  52.         x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
  53.         x = x.view(-1, 320)
  54.         x = F.relu(self.fc1(x))
  55.         x = F.dropout(x, training=self.training)
  56.         x = self.fc2(x)
  57.         return F.log_softmax(x, dim=1)
  60. model = Net().to(device)
  61. data = torch.rand(10, 1, 28, 28).to(device)
  62. model(data)

参考代码：

参考资料：

卷积神经网络之-STN(空间注意力机制）.md