最通俗易懂的二次贝塞尔曲线讲解

原理和简单推导（以三阶为例）：
设P、P、P是一条抛物线上顺序三个不同的点。过P和P点的两切线交于P点，在P点的切线交P__P和P__P于P和P，则如下比例成立：

这是所谓抛物线的三切线定理。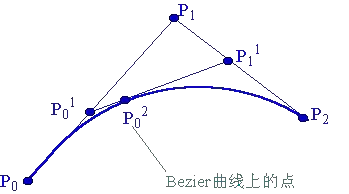

当P，P固定，引入参数t，令上述比值为t:(1-t)，即有：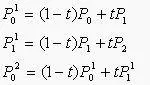

t从0变到1，第一、二式就分别表示控制二边形的第一、二条边，它们是两条一次Bezier曲线。将一、二式代入第三式得：

当t从0变到1时，它表示了由三顶点P、P、P三点定义的一条二次Bezier曲线。
并且表明：
这二次Bezier曲线P可以定义为分别由前两个顶点(P,P)和后两个顶点(P,P)决定的一次Bezier曲线的线性组合。
依次类推，
由四个控制点定义的三次Bezier曲线P可被定义为分别由(P,P,P)和(P,P,P)确定的二条二次Bezier曲线的线性组合，由(_n+_1)个控制点_Pi(_i=0,1,…,n)定义的n次Bezier曲线P__n可被定义为分别由前、后n个控制点定义的两条(n-1)次Bezier曲线P__n-与P__n-的线性组合：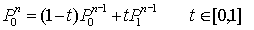

由此得到Bezier曲线的递推计算公式

这就是这就是de Casteljau算法，可以简单阐述三阶贝塞尔曲线原理。
下面是总结：转自http://blog.csdn.net/tianhai110/article/details/2203572
Bézier curve(贝塞尔曲线)是应用于二维图形应用程序的数学曲线。 曲线定义：起始点、终止点（也称锚点）、控制点。通过调整控制点，贝塞尔曲线的形状会发生变化。 1962年，法国数学家Pierre Bézier第一个研究了这种矢量绘制曲线的方法，并给出了详细的计算公式，因此按照这样的公式绘制出来的曲线就用他的姓氏来命名，称为贝塞尔曲线。
以下公式中：B(t)为t时间下 点的坐标；
P为起点,P为终点,P为控制点
一阶贝塞尔曲线(线段)：


意义：由 P0 至 P1 的连续点， 描述的一条线段
二阶贝塞尔曲线(抛物线)：


原理：由 P0 至 P1 的连续点 Q0，描述一条线段。
由 P1 至 P2 的连续点 Q1，描述一条线段。
由 Q0 至 Q1 的连续点 B(t)，描述一条二次贝塞尔曲线。
经验：P1-P0为曲线在P0处的切线。
三阶贝塞尔曲线：


通用公式：

高阶贝塞尔曲线：
4阶曲线：

5阶曲线：

分类: 3D

作者：videring
链接：https://www.jianshu.com/p/afccc4642621
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。