角的 1° = 60’(分) = 3600’’(秒)
180°叫平角，两个角之和90°叫做余角，两个角之和180°叫做补角。
两条直线相交，相邻的两个互补的角叫做邻补角，对顶的角叫对顶角，并且对顶角相等。
在同一个平面内，经过一点有且只有一条直线与已知直线垂直。
一条竖线，穿过两条直线，产生8个角，两个角分别在同一方（上方，下方），同一侧（左侧，右侧）的角，叫做同位角；两个角分别在“两条直线之间”，并且分别在竖线的两侧（一个在左，一个在右），并且不在同一方的角叫做内错角；两个角分别在“两条直线之间”，并且分别在竖线的同一侧（左侧，右侧），并且不在同一方的角叫做旁内角。

求周长

正方形的周长 : C = 边长*4

长方形的周长 | 平行四边形的周长 : C = (长+宽) * 2

多边形的周长 : C = 所有边的长度之和

圆的周长(d为直径，r为半径，π) : C = 2πr = dπ;

扇型的周长

求面积

四边形求面积 = 高 底 = S
梯型求面积 = (上底 + 下底) 高 / 2 = S
长方形求面积 = 长 * 宽 = S

正方形求面积 = 边长 * 边长 = S

三角形求面积 = 底边 * 高 / 2 = S

圆求面积 = πr2 = S

角度制

将圆的1/360作为1度的角记坐1°，这种用度作单位来度量角的单位制叫角度制。

弧度制

将长度等于半径长的弧所对的圆心叫1弧度的角，记作1 rad ｜ 1弧度 ｜ 1.
这种用弧度作单位来度量角的单位制叫做弧度制。

角度于弧度的换算

圆周长 C = 2πr，即c/r = 2π = 360°，π≈3.14=180°
即 π/1 = 180°/n°，1=n°= (180/π)°≈57.3
a/π = 180°/1°, 1° = a = 180/π

三角函数 椭圆

椭圆的定义

平面内某一动点到两个定点的距离之和等于定长的点的轨迹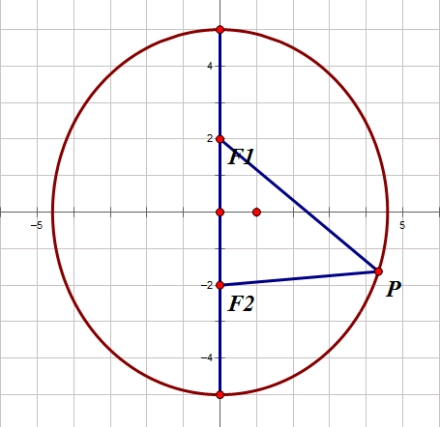
image.png F1,F2 是定点，P是动点
PF1+PF2=2a
F1到P点的距离+F2到P点的距离=2a，这个2a的所有的点的轨迹，形成的图像就是椭圆

  1. sin²θ+cos²θ=1
  2. 因为由三角函数线，cos=x/r,sin=y/r
  3. 所以由x²/a²+x²/b²=1
  4. 令x/a=cosθ,y/b=sinθ
  5. x=acosθ ， y=bsinθ

求圆或椭圆上任意点的位置

圆上任意角度的点的坐标

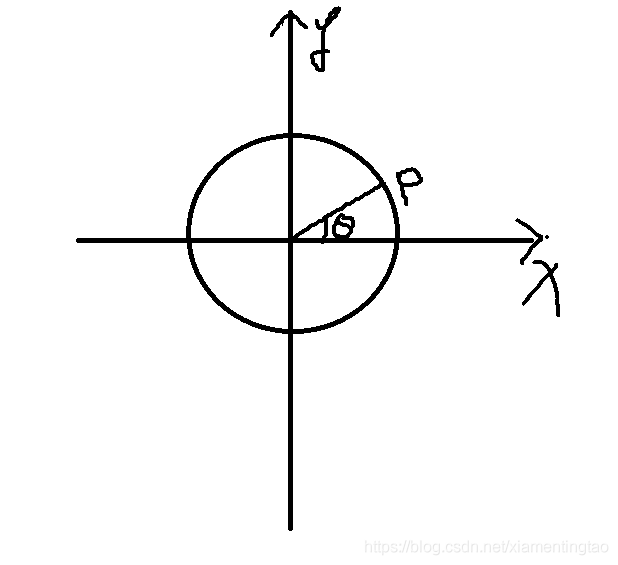
image.png
如上图，给定圆心（Cx,Cy）,半径为R，求θ对应的点的坐标
px=Cx+Rcos(θ)
py=Cy+Rsin(θ)
注意如果以上竖直坐标系向下，此时变为图像的坐标系，即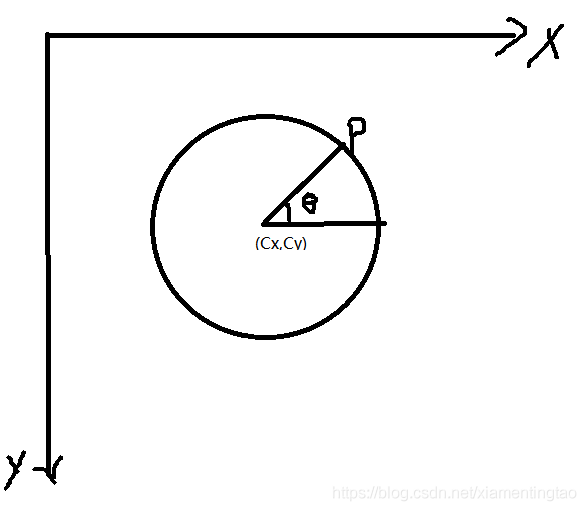
image.png
px=Cx+Rcos(θ)
py=Cy-Rsin(θ)

求椭圆上任意坐标的位置

  1. <!DOCTYPE html>
  2. <html>
  4. <head lang="en">
  5.     <meta charset="UTF-8">
  6.     <title>css3</title>
  7. </head>
  9. <body>
  10.     <style>
  11.         .avatar {
  12.             position: fixed;
  13.             left: 200px;
  14.             top: 200px;
  15.             width: 300px;
  16.             height: 200px;
  17.         }
  18.         .img {
  19.             position: absolute;
  20.             border-radius: 100%;
  21.             width: 20px;
  22.             height: 20px;
  23.             background-color: blue;
  24.         }
  25.         .item {
  26.             position: relative;
  27.             z-index: 2;
  28.             width: 100%;
  29.             height: 100%;
  30.             background-color: rgba(138, 43, 226, 1);
  31.             border-radius: 100%;
  32.         }
  33.     </style>
  35.     <div class="avatar">
  36.         <div class="item"></div>
  37.     </div>
  39.     <script>
  41.         const avatar = document.querySelector('.avatar')
  42.         getCPoint(150, 100, 1, 150 - 10, 100 - 10)
  43.         // a 长半径， b 短半径， p 节点的间隔 ， cx, cy 圆心, 
  44.         function getCPoint (a, b, p = 1, cx = 0, cy = 0) {
  45.             const data = []
  46.             for (let index = 0; index < 360; index = index + p) {
  47.                 let x = a * Math.cos(Math.PI * 2 * index / 360)
  48.                 let y = b * Math.sin(Math.PI * 2 * index / 360)
  50.                 const div = document.createElement('div')
  51.                 div.className = 'img'
  52.                 console.log((x + cx), (y + cy))
  53.                 div.style.left = (x + cx) + 'px';
  54.                 div.style.top = (y + cy) + 'px';
  55.                 avatar.appendChild(div);
  57.             }
  58.         }
  61.     </script>
  62. </body>
  64. </html>