最短路径算法（Dijkstra Floyd）

问题描述

校园最短路径实验

1、给出校园中常用的几个点，如教室550、文宗楼、三个食堂、大操场、宿舍楼（自定）、校门口、体育场；
2、画图并给出其邻接矩阵（请合作完成）；
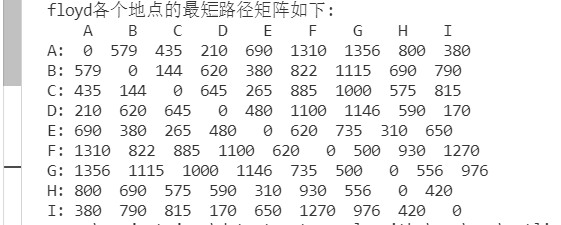
3、用floyd算法求每对顶点间的最短路。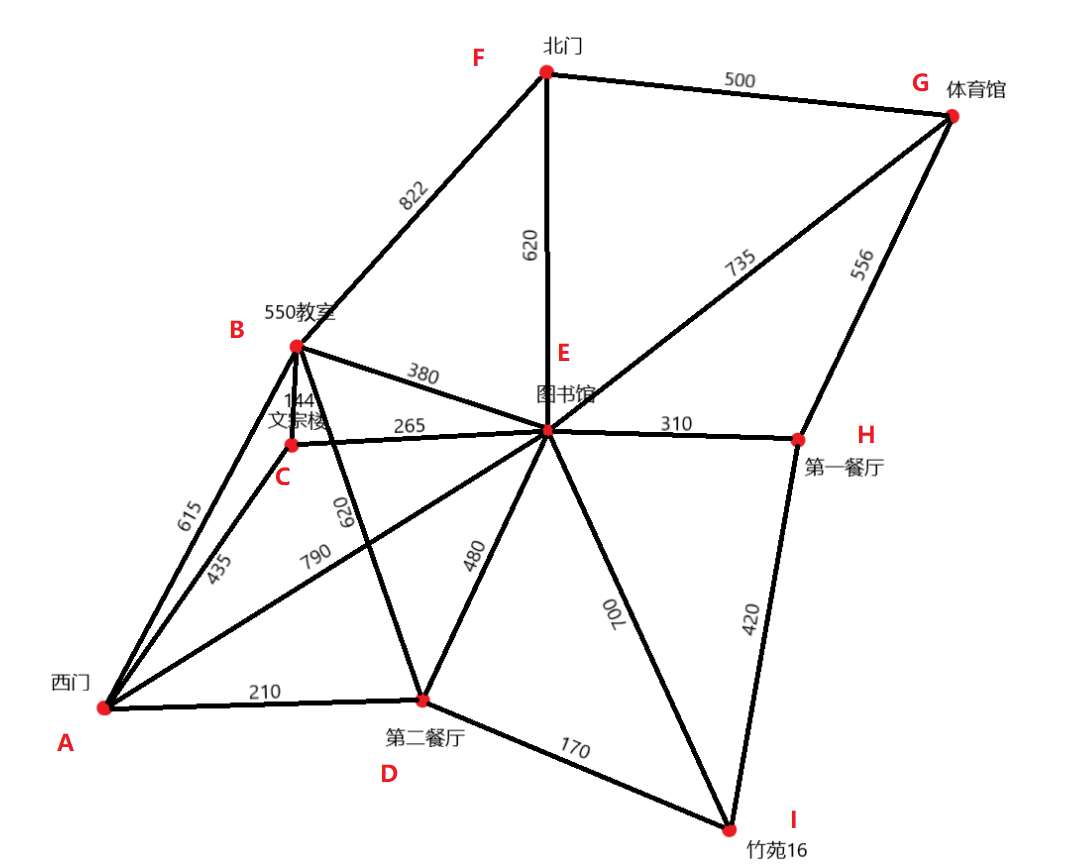

:::tips 迪杰斯特拉（Dijkstra）算法 :::

Dijkstra算法是经典的单源最短路径算法，用于计算源点到其它所有顶点的最短路径。在图 G=(V,E) 中，假设每条边 E[i] 的权值距离为 w[i]，找到由源点 v0 到其余各点的最短路径。
适用：不含负权重的图

算法当中，对图的遍历方式为BFS（广度优先遍历）

代码

/**
 * C++: Floyd算法获取最短路径(邻接矩阵)
 *
 */
#include <iomanip>
#include <iostream>
#include <vector>
#include <bits/stdc++.h>
using namespace std;
// 边的结构体
class EData
{
    public:
        char start; // 边的起点
        char end;   // 边的终点
        int weight; // 边的权重
    public:
        EData(){}
        EData(char s, char e, int w):start(s),end(e),weight(w){}
};
class MatrixUDG {
    #define MAX    100
    #define INF    (~(0x1<<31))        // 无穷大(即0X7FFFFFFF)
    private:
        char mVexs[MAX];    // 顶点集合
        int mVexNum;             // 顶点数
        int mEdgNum;             // 边数
        int mMatrix[MAX][MAX];   // 邻接矩阵
    public:
        // 创建图(自己输入数据)
        MatrixUDG();
        // 创建图(用已提供的矩阵)
        //MatrixUDG(char vexs[], int vlen, char edges[][2], int elen);
        MatrixUDG(char vexs[], int vlen, int matrix[][9]);
        ~MatrixUDG();
        // 深度优先搜索遍历图
        void DFS();
        // 广度优先搜索（类似于树的层次遍历）
        void BFS();
        // prim最小生成树(从start开始生成最小生成树)
        void prim(int start);
        // 克鲁斯卡尔（Kruskal)最小生成树
        void kruskal();
        // Dijkstra最短路径
        void dijkstra(int vs, int vexs[], int dist[]);
        // Floyd最短路径
        void floyd(int path[][MAX], int dist[][MAX]);
        // 打印矩阵队列图
        void print();
    private:
        // 读取一个输入字符
        char readChar();
        // 返回ch在mMatrix矩阵中的位置
        int getPosition(char ch);
        // 返回顶点v的第一个邻接顶点的索引，失败则返回-1
        int firstVertex(int v);
        // 返回顶点v相对于w的下一个邻接顶点的索引，失败则返回-1
        int nextVertex(int v, int w);
        // 深度优先搜索遍历图的递归实现
        void DFS(int i, int *visited);
        // 获取图中的边
        EData* getEdges();
        // 对边按照权值大小进行排序(由小到大)
        void sortEdges(EData* edges, int elen);
        // 获取i的终点
        int getEnd(int vends[], int i);
};
/* 
 * 创建图(自己输入数据)
 */
MatrixUDG::MatrixUDG()
{
    char c1, c2;
    int i, j, weight, p1, p2;
    // 输入"顶点数"和"边数"
    cout << "input vertex number: ";
    cin >> mVexNum;
    cout << "input edge number: ";
    cin >> mEdgNum;
    if ( mVexNum < 1 || mEdgNum < 1 || (mEdgNum > (mVexNum * (mVexNum-1))))
    {
        cout << "input error: invalid parameters!" << endl;
        return ;
    }
    // 初始化"顶点"
    for (i = 0; i < mVexNum; i++)
    {
        cout << "vertex(" << i << "): ";
        mVexs[i] = readChar();
    }
    // 1. 初始化"边"的权值
    for (i = 0; i < mVexNum; i++)
    {
        for (j = 0; j < mVexNum; j++)
        {
            if (i==j)
                mMatrix[i][j] = 0;
            else
                mMatrix[i][j] = INF;
        }
    }
    // 2. 初始化"边"的权值: 根据用户的输入进行初始化
    for (i = 0; i < mEdgNum; i++)
    {
        // 读取边的起始顶点，结束顶点，权值
        cout << "edge(" << i << "): ";
        c1 = readChar();
        c2 = readChar();
        cin >> weight;
        p1 = getPosition(c1);
        p2 = getPosition(c2);
        if (p1==-1 || p2==-1)
        {
            cout << "input error: invalid edge!" << endl;
            return ;
        }
        mMatrix[p1][p2] = weight;
        mMatrix[p2][p1] = weight;
    }
}
/*
 * 创建图(用已提供的矩阵)
 *
 * 参数说明：
 *     vexs  -- 顶点数组
 *     vlen  -- 顶点数组的长度
 *     matrix-- 矩阵(数据)
 */
MatrixUDG::MatrixUDG(char vexs[], int vlen, int matrix[][9])
{
    int i, j;
    // 初始化"顶点数"和"边数"
    mVexNum = vlen;
    // 初始化"顶点"
    for (i = 0; i < mVexNum; i++)
        mVexs[i] = vexs[i];
    // 初始化"边"
    for (i = 0; i < mVexNum; i++)
        for (j = 0; j < mVexNum; j++)
            mMatrix[i][j] = matrix[i][j];
    // 统计边的数目
    for (i = 0; i < mVexNum; i++)
        for (j = 0; j < mVexNum; j++)
            if (i!=j && mMatrix[i][j]!=INF)
                mEdgNum++;
    mEdgNum /= 2;
}
/* 
 * 析构函数
 */
MatrixUDG::~MatrixUDG() 
{
}
/*
 * 返回ch在mMatrix矩阵中的位置
 */
int MatrixUDG::getPosition(char ch)
{
    int i;
    for(i=0; i<mVexNum; i++)
        if(mVexs[i]==ch)
            return i;
    return -1;
}
/*
 * 读取一个输入字符
 */
char MatrixUDG::readChar()
{
    char ch;
    do {
        cin >> ch;
    } while(!((ch>='a'&&ch<='z') || (ch>='A'&&ch<='Z')));
    return ch;
}
/*
 * 返回顶点v的第一个邻接顶点的索引，失败则返回-1
 */
int MatrixUDG::firstVertex(int v)
{
    int i;
    if (v<0 || v>(mVexNum-1))
        return -1;
    for (i = 0; i < mVexNum; i++)
        if (mMatrix[v][i]!=0 && mMatrix[v][i]!=INF)
            return i;
    return -1;
}
/*
 * 返回顶点v相对于w的下一个邻接顶点的索引，失败则返回-1
 */
int MatrixUDG::nextVertex(int v, int w)
{
    int i;
    if (v<0 || v>(mVexNum-1) || w<0 || w>(mVexNum-1))
        return -1;
    for (i = w + 1; i < mVexNum; i++)
        if (mMatrix[v][i]!=0 && mMatrix[v][i]!=INF)
            return i;
    return -1;
}
/*
 * 深度优先搜索遍历图的递归实现
 */
void MatrixUDG::DFS(int i, int *visited)
{
    int w;
    visited[i] = 1;
    cout << mVexs[i] << " ";
    // 遍历该顶点的所有邻接顶点。若是没有访问过，那么继续往下走
    for (w = firstVertex(i); w >= 0; w = nextVertex(i, w))
    {
        if (!visited[w])
            DFS(w, visited);
    }
}
/*
 * 深度优先搜索遍历图
 */
void MatrixUDG::DFS()
{
    int i;
    int visited[MAX];       // 顶点访问标记
    // 初始化所有顶点都没有被访问
    for (i = 0; i < mVexNum; i++)
        visited[i] = 0;
    cout << "DFS: ";
    for (i = 0; i < mVexNum; i++)
    {
        //printf("\n== LOOP(%d)\n", i);
        if (!visited[i])
            DFS(i, visited);
    }
    cout << endl;
}
/*
 * 广度优先搜索（类似于树的层次遍历）
 */
void MatrixUDG::BFS()
{
    int head = 0;
    int rear = 0;
    int queue[MAX];     // 辅组队列
    int visited[MAX];   // 顶点访问标记
    int i, j, k;
    for (i = 0; i < mVexNum; i++)
        visited[i] = 0;
    cout << "BFS: ";
    for (i = 0; i < mVexNum; i++)
    {
        if (!visited[i])
        {
            visited[i] = 1;
            cout << mVexs[i] << " ";
            queue[rear++] = i;  // 入队列
        }
        while (head != rear) 
        {
            j = queue[head++];  // 出队列
            for (k = firstVertex(j); k >= 0; k = nextVertex(j, k)) //k是为访问的邻接顶点
            {
                if (!visited[k])
                {
                    visited[k] = 1;
                    cout << mVexs[k] << " ";
                    queue[rear++] = k;
                }
            }
        }
    }
    cout << endl;
}
/*
 * 打印矩阵队列图
 */
void MatrixUDG::print()
{
    int i,j;
    cout << "Martix Graph:" << endl;
    for (i = 0; i < mVexNum; i++)
    {
        for (j = 0; j < mVexNum; j++)
            cout << setw(10) << mMatrix[i][j] << " ";
        cout << endl;
    }
}
/*
 * prim最小生成树
 *
 * 参数说明：
 *   start -- 从图中的第start个元素开始，生成最小树
 */
void MatrixUDG::prim(int start)
{
    int min,i,j,k,m,n,sum;
    int index=0;         // prim最小树的索引，即prims数组的索引
    char prims[MAX];     // prim最小树的结果数组
    int weights[MAX];    // 顶点间边的权值
    // prim最小生成树中第一个数是"图中第start个顶点"，因为是从start开始的。
    prims[index++] = mVexs[start];
    // 初始化"顶点的权值数组"，
    // 将每个顶点的权值初始化为"第start个顶点"到"该顶点"的权值。
    for (i = 0; i < mVexNum; i++ )
        weights[i] = mMatrix[start][i];
    // 将第start个顶点的权值初始化为0。
    // 可以理解为"第start个顶点到它自身的距离为0"。
    weights[start] = 0;
    for (i = 0; i < mVexNum; i++)
    {
        // 由于从start开始的，因此不需要再对第start个顶点进行处理。
        if(start == i)
            continue;
        j = 0;
        k = 0;
        min = INF;
        // 在未被加入到最小生成树的顶点中，找出权值最小的顶点。
        while (j < mVexNum)
        {
            // 若weights[j]=0，意味着"第j个节点已经被排序过"(或者说已经加入了最小生成树中)。
            if (weights[j] != 0 && weights[j] < min)
            {
                min = weights[j];
                k = j;
            }
            j++;
        }
        // 经过上面的处理后，在未被加入到最小生成树的顶点中，权值最小的顶点是第k个顶点。
        // 将第k个顶点加入到最小生成树的结果数组中
        prims[index++] = mVexs[k];
        // 将"第k个顶点的权值"标记为0，意味着第k个顶点已经排序过了(或者说已经加入了最小树结果中)。
        weights[k] = 0;
        // 当第k个顶点被加入到最小生成树的结果数组中之后，更新其它顶点的权值。
        for (j = 0 ; j < mVexNum; j++)
        {
            // 当第j个节点没有被处理，并且需要更新时才被更新。
            if (weights[j] != 0 && mMatrix[k][j] < weights[j])
                weights[j] = mMatrix[k][j];
        }
    }
    // 计算最小生成树的权值
    sum = 0;
    for (i = 1; i < index; i++)
    {
        min = INF;
        // 获取prims[i]在mMatrix中的位置
        n = getPosition(prims[i]);
        // 在vexs[0...i]中，找出到j的权值最小的顶点。
        for (j = 0; j < i; j++)
        {
            m = getPosition(prims[j]);
            if (mMatrix[m][n]<min)
                min = mMatrix[m][n];
        }
        sum += min;
    }
    // 打印最小生成树
    cout << "PRIM(" << mVexs[start] << ")=" << sum << ": ";
    for (i = 0; i < index; i++)
        cout << prims[i] << " ";
    cout << endl;
}
/* 
 * 获取图中的边
 */
EData* MatrixUDG::getEdges()
{
    int i,j;
    int index=0;
    EData *edges;
    edges = new EData[mEdgNum];
    for (i=0; i < mVexNum; i++)
    {
        for (j=i+1; j < mVexNum; j++)
        {
            if (mMatrix[i][j]!=INF)
            {
                edges[index].start  = mVexs[i];
                edges[index].end    = mVexs[j];
                edges[index].weight = mMatrix[i][j];
                index++;
            }
        }
    }
    return edges;
}
/* 
 * 对边按照权值大小进行排序(由小到大)
 */
void MatrixUDG::sortEdges(EData* edges, int elen)
{
    int i,j;
    for (i=0; i<elen; i++)
    {
        for (j=i+1; j<elen; j++)
        {
            if (edges[i].weight > edges[j].weight)
            {
                // 交换"边i"和"边j"
                swap(edges[i], edges[j]);
            }
        }
    }
}
/*
 * 获取i的终点
 */
int MatrixUDG::getEnd(int vends[], int i)
{
    while (vends[i] != 0)
        i = vends[i];
    return i;
}
/*
 * 克鲁斯卡尔（Kruskal)最小生成树
 */
void MatrixUDG::kruskal()
{
    int i,m,n,p1,p2;
    int length;
    int index = 0;          // rets数组的索引
    int vends[MAX]={0};     // 用于保存"已有最小生成树"中每个顶点在该最小树中的终点。
    EData rets[MAX];        // 结果数组，保存kruskal最小生成树的边
    EData *edges;           // 图对应的所有边
    // 获取"图中所有的边"
    edges = getEdges();
    // 将边按照"权"的大小进行排序(从小到大)
    sortEdges(edges, mEdgNum);
    for (i=0; i<mEdgNum; i++)
    {
        p1 = getPosition(edges[i].start);      // 获取第i条边的"起点"的序号
        p2 = getPosition(edges[i].end);        // 获取第i条边的"终点"的序号
        m = getEnd(vends, p1);                 // 获取p1在"已有的最小生成树"中的终点
        n = getEnd(vends, p2);                 // 获取p2在"已有的最小生成树"中的终点
        // 如果m!=n，意味着"边i"与"已经添加到最小生成树中的顶点"没有形成环路
        if (m != n)
        {
            vends[m] = n;                       // 设置m在"已有的最小生成树"中的终点为n
            rets[index++] = edges[i];           // 保存结果
        }
    }
    delete[] edges;
    // 统计并打印"kruskal最小生成树"的信息
    length = 0;
    for (i = 0; i < index; i++)
        length += rets[i].weight;
    cout << "Kruskal=" << length << ": ";
    for (i = 0; i < index; i++)
        cout << "(" << rets[i].start << "," << rets[i].end << ") ";
    cout << endl;
}
/*
 * Dijkstra最短路径。
 * 即，统计图中"顶点vs"到其它各个顶点的最短路径。
 *
 * 参数说明：
 *       vs -- 起始顶点(start vertex)。即计算"顶点vs"到其它顶点的最短路径。
 *     prev -- 前驱顶点数组。即，prev[i]的值是"顶点vs"到"顶点i"的最短路径所经历的全部顶点中，位于"顶点i"之前的那个顶点。
 *     dist -- 长度数组。即，dist[i]是"顶点vs"到"顶点i"的最短路径的长度。
 */
void MatrixUDG::dijkstra(int vs, int prev[], int dist[])
{
    int i,j,k;
    int min;
    int tmp;
    int flag[MAX];      // flag[i]=1表示"顶点vs"到"顶点i"的最短路径已成功获取。
    // 初始化
    for (i = 0; i < mVexNum; i++)
    {
        flag[i] = 0;              // 顶点i的最短路径还没获取到。
        prev[i] = 0;              // 顶点i的前驱顶点为0。
        dist[i] = mMatrix[vs][i]; // 顶点i的最短路径为"顶点vs"到"顶点i"的权。
    }
    // 对"顶点vs"自身进行初始化
    flag[vs] = 1;
    dist[vs] = 0;
    // 遍历mVexNum-1次；每次找出一个顶点的最短路径。
    for (i = 1; i < mVexNum; i++)
    {
        // 寻找当前最小的路径；
        // 即，在未获取最短路径的顶点中，找到离vs最近的顶点(k)。
        min = INF;
        for (j = 0; j < mVexNum; j++)
        {
            if (flag[j]==0 && dist[j]<min)
            {
                min = dist[j];
                k = j;
            }
        }
        // 标记"顶点k"为已经获取到最短路径
        flag[k] = 1;
        // 修正当前最短路径和前驱顶点
        // 即，当已经"顶点k的最短路径"之后，更新"未获取最短路径的顶点的最短路径和前驱顶点"。
        for (j = 0; j < mVexNum; j++)
        {
            tmp = (mMatrix[k][j]==INF ? INF : (min + mMatrix[k][j]));
            if (flag[j] == 0 && (tmp  < dist[j]) )
            {
                dist[j] = tmp;
                prev[j] = k;
            }
        }
    }
    // 打印dijkstra最短路径的结果
    cout << "dijkstra(" << mVexs[vs] << "): " << endl;
    for (i = 0; i < mVexNum; i++)
        cout << "  shortest(" << mVexs[vs] << ", " << mVexs[i] << ")=" << dist[i] << endl;
}
/*
 * floyd最短路径。
 * 即，统计图中各个顶点间的最短路径。
 *
 * 参数说明：
 *     path -- 路径。path[i][j]=k表示，"顶点i"到"顶点j"的最短路径会经过顶点k。
 *     dist -- 长度数组。即，dist[i][j]=sum表示，"顶点i"到"顶点j"的最短路径的长度是sum。
 */
void MatrixUDG::floyd(int path[][MAX], int dist[][MAX])
{
    int i,j,k;
    int tmp;
    // 初始化
    for (i = 0; i < mVexNum; i++)
    {
        for (j = 0; j < mVexNum; j++)
        {
            dist[i][j] = mMatrix[i][j];    // "顶点i"到"顶点j"的路径长度为"i到j的权值"。
            path[i][j] = j;                // "顶点i"到"顶点j"的最短路径是经过顶点j。
        }
    }
    // 计算最短路径
    for (k = 0; k < mVexNum; k++)
    {
        for (i = 0; i < mVexNum; i++)
        {
            for (j = 0; j < mVexNum; j++)
            {
                // 如果经过下标为k顶点路径比原两点间路径更短，则更新dist[i][j]和path[i][j]
                tmp = (dist[i][k]==INF || dist[k][j]==INF) ? INF : (dist[i][k] + dist[k][j]);
                if (dist[i][j] > tmp)
                {
                    // "i到j最短路径"对应的值设，为更小的一个(即经过k)
                    dist[i][j] = tmp;
                    // "i到j最短路径"对应的路径，经过k
                    path[i][j] = path[i][k];
                }
            }
        }
    }
    char dot[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I'};
    // 打印floyd最短路径的结果
    cout << "floyd各个地点的最短路径矩阵如下: " << endl;
    cout << "    ";
    for (int k = 0;k<9;k++){
        cout << dot[k] << "    ";
    }
    cout << "\n";
    for (i = 0; i < mVexNum; i++){
        cout << dot[i] << ": ";
        for (j = 0; j < mVexNum; j++)
            cout << setw(2) << dist[i][j] << "  ";
        cout << endl;
    }
}
int main()
{
    int prev[MAX] = {0};
    int dist[MAX] = {0};
    int path[MAX][MAX] = {0};    // 用于保存floyd路径
    int floy[MAX][MAX] = {0};    // 用于保存floyd长度
    char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I'};
    int matrix[][9] = {
                      /*A*//*B*//*C*//*D*//*E*//*F*//*G*//*H*//*I*/
      /*A西门*/     {   0,  615, 435, 210, 790,  INF,  INF, INF, INF},
      /*B550教室*/  { 615,   0,  144, 620, 380,   822, INF, INF, INF},
      /*C文宗楼*/   { 435,  144,   0,   INF,   265,   INF, INF, INF, INF},
      /*D二餐*/     { 210, 620,   INF,   0,   480, INF, INF, INF, 170},
      /*E图书馆*/   { 790, 380,   265,   480,   0,   620,   735, 310, 700},
      /*F北门*/     { INF, 822,   INF,   INF,   620,   0,   500, INF, INF},
      /*G体育馆*/   { INF, INF,   INF,   INF,   735,   500,   0, 556, INF},
      /*H一餐*/     {  INF,   INF,   INF, INF,   310,   INF,   556, 0, 420},
      /*I16号楼*/   {  INF, INF, INF, 170,   700,   INF,   INF, 420, 0}};
    int vlen = sizeof(vexs)/sizeof(vexs[0]);
    MatrixUDG* pG;
    // 自定义"图"(输入矩阵队列)
    //pG = new MatrixUDG();
    // 采用已有的"图"
    pG = new MatrixUDG(vexs, vlen, matrix);
    //pG->print();   // 打印图
    //pG->DFS();     // 深度优先遍历
    //pG->BFS();     // 广度优先遍历
    //pG->prim(0);   // prim算法生成最小生成树
    //pG->kruskal(); // Kruskal算法生成最小生成树
    // dijkstra算法获取"第4个顶点"到其它各个顶点的最短距离
    //pG->dijkstra(3, prev, dist);
    // floyd算法获取各个顶点之间的最短距离
    pG->floyd(path, floy);
    return 0;
}

参考

• 图最短路径算法之迪杰斯特拉算法（Dijkstra）
• Floyd算法(二)之 C++详解