Problems - 实验5——波兰/逆波兰表达式求值🔖栈 - 《技术博客》

实验报告
思路
实验代码
include

实验报告

实验五：实现用波兰表达式（先序）和逆波兰表达式（后序）求算术表达式的值
要求：仅用一个栈实现（并且用原生单链表实现）
测试用例：4+2*3-10/5
交作业时间：5月14日

思路

两个步骤：

将给定的表达式转换为波兰表达式/逆波兰表达式
对转换后的式子进行计算

学习遍历二叉树，利用前序/中序/后序表达式的时候，经常有一个问题就是：

给出中缀表达式，【写出&&编程出】后序（逆波兰）表达式

上面的是课堂上在纸上的书写，那么如何将其用编程语言实现呢？思路应该是这样的：

遍历表达式：对遍历的元素进行判断
是运算符？操作数？还是括号呢？对其相应的判断
- 操作数
- 运算符：+-*/
- 括号
[x] 个位数/双位数……的字符处理
[x] 给出中缀表达式，【写出&&编程出】前序（波兰）表达式

如果写出了逆波兰表达式，转换为波兰表达式只需要将（变为），同时遍历从后往前遍历即可

最后的结果逆置

最后的计算，波兰和逆波兰不能写成一个函数，因为减数和被减数，除数和被除数的缘故
实验代码

```cpp
include
using namespace std;

/**

波兰表达式/逆波兰表达式求解运算表达式
*/

/**

单链表的存储结构 / typedef struct LNode { string data; //数据域 struct LNode next; //指针域 }Lnode, *LinkList; //LinkList为指向结构体LNode的指针类型

/ 初始化链表 / void InitList(LinkList &L) { L = new LNode; L->next = NULL; }

/ 打印 / void TraverseList(LinkList & L){ LNode *p = new LNode; p = L->next; // cout << “此中缀表达式链表打印的结果为：”; while (p != NULL) { cout << p->data; p = p->next; } cout << “\n”; }

/ 逆置 / void ReverseList(LinkList &L) { LNode p = L->next;
L->next = NULL;
while(p)
{ LNode q = p->next;
p->next = L->next;
L->next = p;
p = q;
} }

/**

初始化用户输入的链表 */ void Center(LinkList &L,string s) { InitList(L); LinkList p = L; string temp = “”; for (int i = 0; i < s.length();i++){

 // 处理双位数字情况
 if (isdigit(s[i])) {
     // 该字符为数字
     temp = temp + s[i];
     if (!isdigit(s[i+1])) {
         // 下一个不是数字，而是字符，将temp后插
         LinkList node = new LNode;
         node->data = temp;
         node->next = NULL;
         p->next = node;
         p = node;
         // 将temp重置
         temp = "";
         continue;
     }
     continue;
 }
 // 后插到L尾巴上
 LinkList node = new LNode;
 node->data = s[i];
 node->next = NULL;
 p->next = node;
 p = node;

}
}

/**

将表达式转换为波兰表达式/逆波兰表达式
第二个参数对逆波兰而言是左括号，第三个参数对逆波兰而言是右括号

对波兰而言反过来 */ void Transition(LinkList &L, string l, string r){ // 定义一个栈用来处理 stack stack; LinkList p = L->next; LinkList result = new LNode; InitList(result); LinkList result_a = result;

while(p != NULL) {

 if (p->data == l) {
     stack.push(p->data);
 } else if(p->data == r) {
     while(stack.top() != l){
         LinkList temp = new LNode;
         temp->data = stack.top();
         temp->next = NULL;
         result_a->next = temp;
         result_a = temp;
         stack.pop();
     }
     if (stack.top() == l){
         stack.pop();
     }
 } else if(p->data == "+" || p->data == "-") {
     if (stack.size() != 0) {
         if (stack.top() == "*" || stack.top() == "/"){
             for (int i = 0; i < stack.size();i++) {
                 if (stack.top() == l) {
                     break;
                 }
                 LinkList temp = new LNode;
                 temp->data = stack.top();
                 temp->next = NULL;
                 result_a->next = temp;
                 result_a = temp;
                 stack.pop();
             }
         }
     }
     stack.push(p->data);
 } else if(p->data == "*" || p->data == "/") {
     stack.push(p->data);
 } else {
     LinkList temp = new LNode;
     temp->data = p->data;
     temp->next = NULL;
     result_a->next = temp;
     result_a = temp;
 }
 p = p->next;

} // TraverseList(result); for (int i = 0; i < stack.size();i++) {

 LinkList temp = new LNode;
 temp->data = stack.top();
 temp->next = NULL;
 result_a->next = temp;
 result_a = temp;
 stack.pop();

} // 上一个操作总是不能清空栈的最后一个元素 LinkList temp = new LNode; temp->data = stack.top(); temp->next = NULL; result_a->next = temp; result_a = temp; stack.pop();

L = result; }

/**

计算 */

void EvaulTree(LinkList &L) { // 定义一个栈用来处理 stack stack; LinkList p = L->next; while(p != NULL) { if (p->data == “+”){ int x = stoi(stack.top()); stack.pop(); int y = stoi(stack.top()); stack.pop(); stack.push(to_string(y + x)); } else if(p->data == “-“) { int x = stoi(stack.top()); stack.pop(); int y = stoi(stack.top()); stack.pop(); stack.push(to_string(y - x)); } else if(p->data == ““) { int x = stoi(stack.top()); stack.pop(); int y = stoi(stack.top()); stack.pop(); stack.push(to_string(y x)); } else if(p->data == “/“) { int x = stoi(stack.top()); stack.pop(); int y = stoi(stack.top()); stack.pop(); stack.push(to_string(y / x)); } else { stack.push(p->data); } p = p->next; } while (!stack.empty()){ cout << stoi(stack.top()); stack.pop(); } }

void EvaulTree_polish(LinkList &L) { // 定义一个栈用来处理 stack stack; LinkList p = L->next; while(p != NULL) { if (p->data == “+”){ int x = stoi(stack.top()); stack.pop(); int y = stoi(stack.top()); stack.pop(); stack.push(to_string(x + y)); } else if(p->data == “-“) { int x = stoi(stack.top()); stack.pop(); int y = stoi(stack.top()); stack.pop(); stack.push(to_string(x - y)); } else if(p->data == ““) { int x = stoi(stack.top()); stack.pop(); int y = stoi(stack.top()); stack.pop(); stack.push(to_string(x y)); } else if(p->data == “/“) { int x = stoi(stack.top()); stack.pop(); int y = stoi(stack.top()); stack.pop(); stack.push(to_string(x / y)); } else { stack.push(p->data); } p = p->next; } while (!stack.empty()){ cout << stoi(stack.top()); stack.pop(); } }

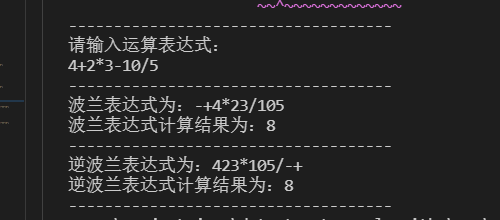
int main () { cout << “——————————————————“<<”\n”; string s; cout << “请输入运算表达式：”<<”\n”; cin >> s; LinkList test_reversepolish = new LNode; InitList(test_reversepolish); LinkList test_polish = new LNode; InitList(test_polish);

Center(test_reversepolish, s);
Center(test_polish, s);
cout << "------------------------------------"<<"\n";
// 波兰表达式
ReverseList(test_polish);
Transition(test_polish, ")", "(");
cout << "波兰表达式为：";
ReverseList(test_polish);
TraverseList(test_polish);
cout << "波兰表达式计算结果为：";
ReverseList(test_polish);
EvaulTree_polish(test_polish);
cout << "\n"<<"------------------------------------"<<"\n";
// 逆波兰表达式
Transition(test_reversepolish, "(", ")");
cout << "逆波兰表达式为：";
TraverseList(test_reversepolish);
cout << "逆波兰表达式计算结果为：";
EvaulTree(test_reversepolish);
cout << "\n"<<"------------------------------------"<<"\n";

} ```

实验5——波兰/逆波兰表达式求值🔖栈

实验报告

思路

实验代码

include