各类排序算法汇总

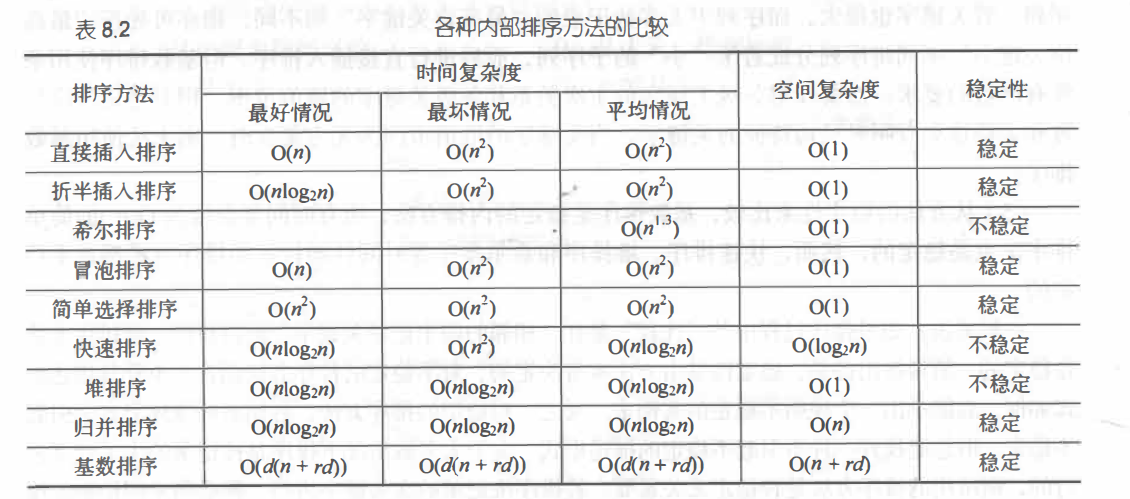
前言：排序按照所占用的计算机内部存储设备，可以分为：内部排序和外部排序

• 内部排序：占用的是内存，待排序序列全部放在内存加以排序处理
• 外部排序：占用的是外存，数据量比较大，内存空间不足以一次性全部容纳数据的情况

本文章 通过912. 排序数组 题目，以此来总结内部排序的各种排序算法。

一、插入类排序

将无序的子序列插入到有序序列中

✅直接插入

将元素序列走一遍，走到某个元素时，将其插入到已走过的已排序序列中，这样可以保证走完所有元素，然后所有的元素都是排序好的。
数据结构选用的时顺序表

/**
* @param {number[]} nums
* @return {number[]}
*/
var sortArray = function(nums) {
  for (let i = 0; i<nums.length; i++) {
    let flag = i
    for(let j = flag-1;j>=0;j--) {
      if (nums[flag] < nums[j]) {
        let temp = nums[j]
        nums[j] = nums[flag]
        nums[flag] = temp
        flag--
      } 
    }
  }
  return nums
};

优化：折半插入

在直接插入的过程中，找到一个元素，然后再需要从后往前依次查找“该在”的位置，对其查找进行了折半优化

/* 折半插入排序 */
void BinsertSort(SqList &S) {
    for (int i = 2; i <= S.length;i++) {
        S.data[0] = S.data[i];
        int low = 1;
        int high = i - 1;
        while (low <= high) {
            int m = (low + high) / 2;
            if (S.data[0]<S.data[m]) high = m - 1;
            else low = m + 1;
        }
        int j;
        for (j = i - 1; j >= high + 1;--j)
            S.data[j + 1] = S.data[j];
        S.data[high + 1] = S.data[0];
    }
}

优化：希尔排序

/* 希尔排序 */
void ShellInsert (SqList &L, int dk) {
    for (int i = dk + 1; i <= L.length;++i) {
        if (L.data[i]<L.data[i-dk]) {
            L.data[0] = L.data[i];
            int j;
            for (j = i - dk; j > 0 && L.data[0] < L.data[j]; j -= dk)
                L.data[j + dk] = L.data[j];
            L.data[j + dk] = L.data[0];
        }
    }
}
void ShellSort (SqList &L, int dt[],int t) {
    for (int k = 0; k < t;++k) {
        ShellInsert(L, dt[k]);
    }
}

二、交换类排序

✅冒泡排序

/**
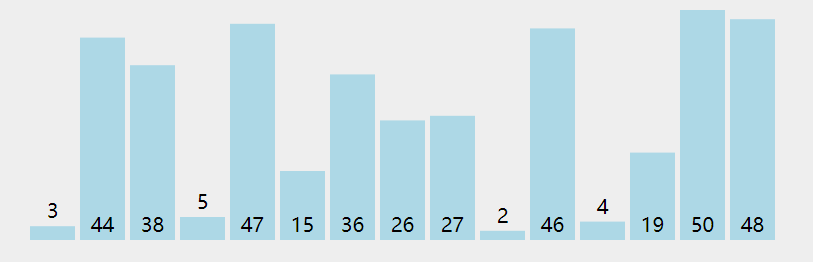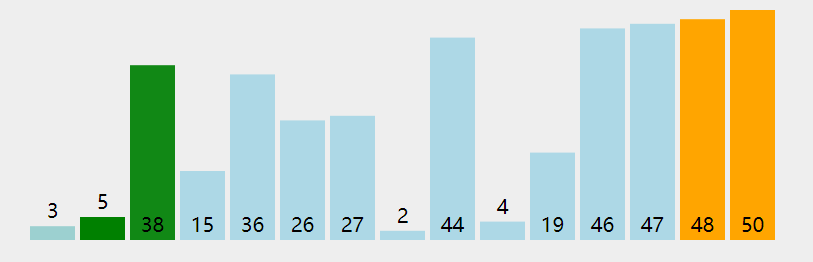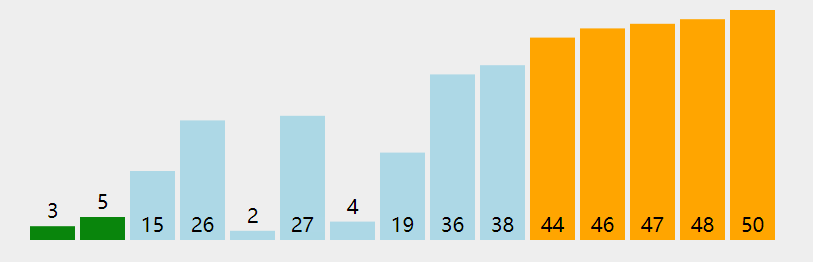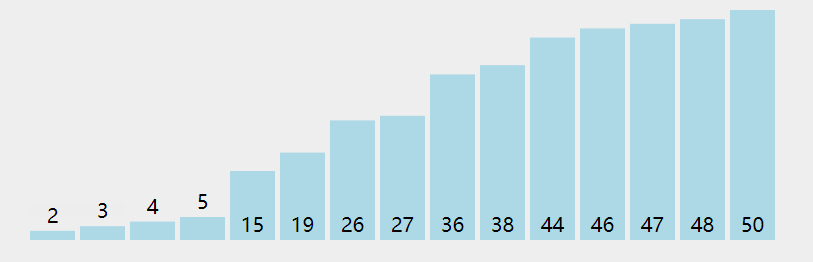
 * @param {number[]} nums
 * @return {number[]}
 */
var sortArray = function(nums) {
    for (let i = nums.length - 1; i>0; i--) {
        for (let j = 0; j<i; j++) {
            if (nums[j] > nums[j+1]) {
                let temp = nums[j]
                nums[j] = nums[j+1]
                nums[j+1] = temp
            }
        }
    }
    return nums
};

快速排序

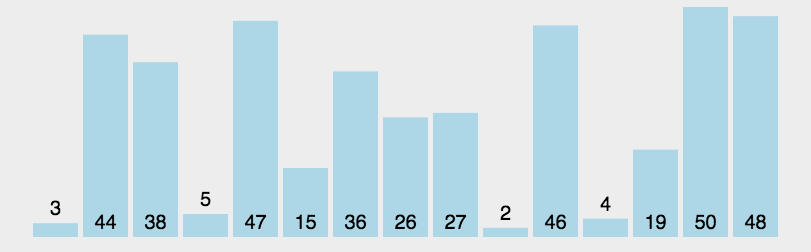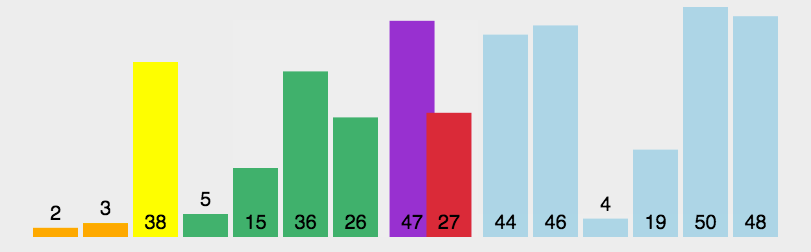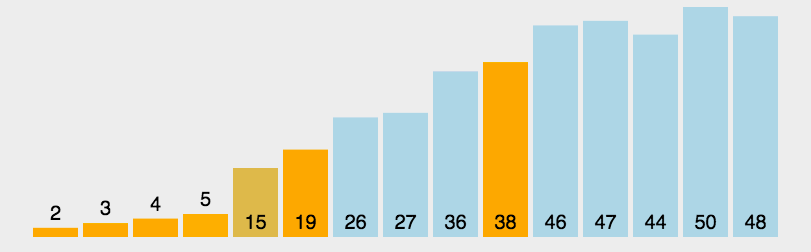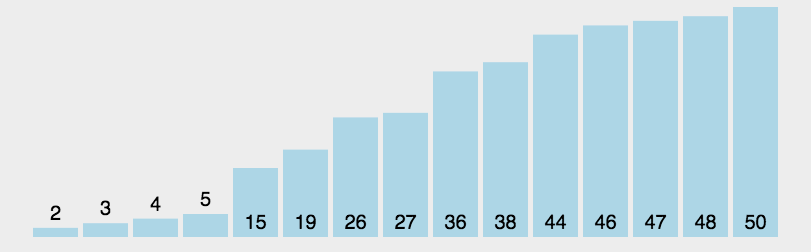
/* 快速排序 */
int Partition (SqList &L, int low, int high) {
    L.data[0] = L.data[low];
    int pivotkey = L.data[low];
    while (low < high) {
        while (low<high && L.data[high]>=pivotkey)
            --high;
        L.data[low] = L.data[high];
        while (low<high && L.data[low]<=pivotkey)
            ++low;
        L.data[high] = L.data[low];
    }
    L.data[low] = L.data[0];
    return low;
}
void Qsort(SqList &L, int low, int high) {
    if (low<high){
        int pivoloc = Partition(L, low, high);
        Qsort(L, low, pivoloc - 1);
        Qsort(L, pivoloc + 1, high);
    }
}
void QuickSort(SqList &L) {
    Qsort(L, 1, L.length);
}

三、选择类排序

参考：ata.biancheng.net/view/72.html

✅简单选择排序

/**
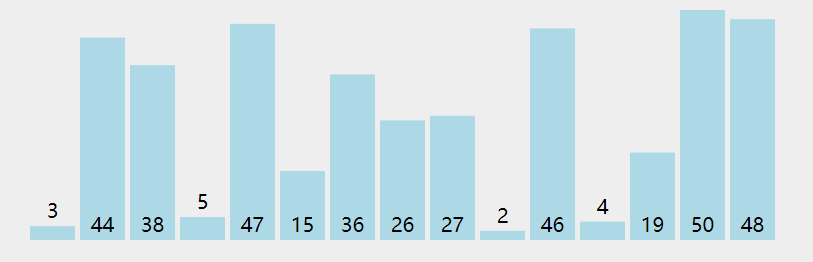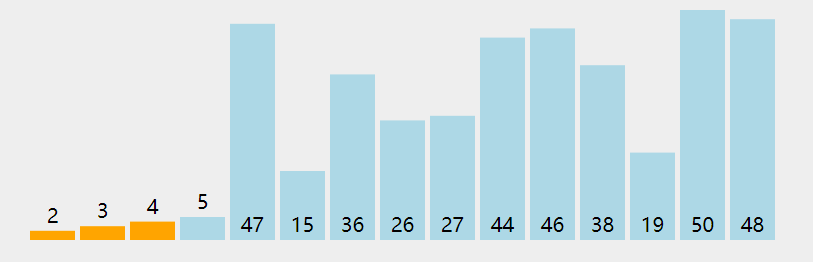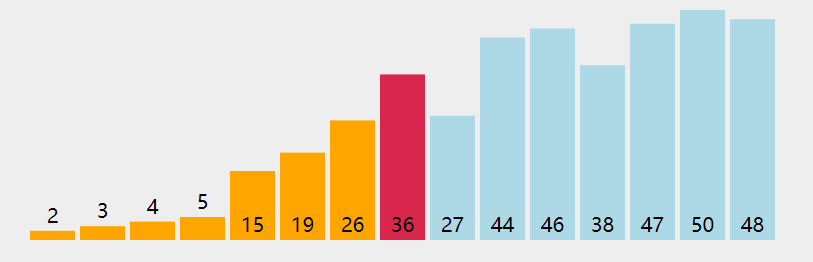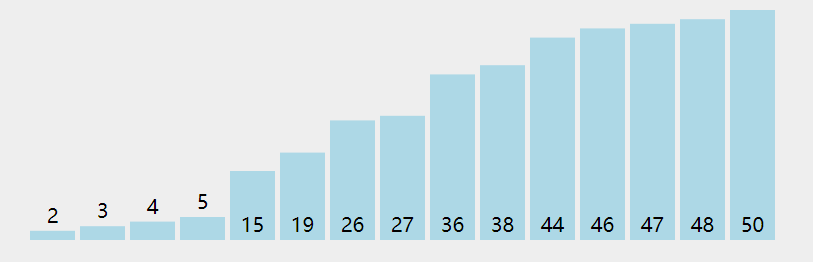
 * @param {number[]} nums
 * @return {number[]}
 */
var sortArray = function(nums) {
    for (let i = 0; i<nums.length-1; i++) {
        for (let j = i+1; j<nums.length; j++) {
            if (nums[i] > nums[j]) {
                let temp = nums[i]
                nums[i] = nums[j]
                nums[j] = temp
            }
        }
    }
    return nums
};

树形选择排序

堆排序

四、归并排序

2-路归并排序

给定一个序列，从左往右两两子序列进行归并

子序列归并的算法：加入有两个靠着的a、b序列，由上面可知，a、b各自都是有序序列，现在就是将这两个合并为一个有序序列k，将a和b序列的各个元素进行比较，小的依次放入k序列，当a、b两个中有一个序列为空了，就将那个不为空的序列直接加入到k序列即可，最后k序列就是目的序列。

五、分配类排序

基数排序

TODO: 扑克牌的花色排序

六、外部排序

基本方法

多路平衡归并

基本思想是内部排序中的2-路归并排序

置换-选择排序

最佳归并树

参考

文章的动画演示

• https://blog.csdn.net/Hk_john/article/details/79888992（js）
• https://www.itrhx.com/2020/10/23/A91-sorting-algorithm/（python）