ANN神经网络

一、基本结构

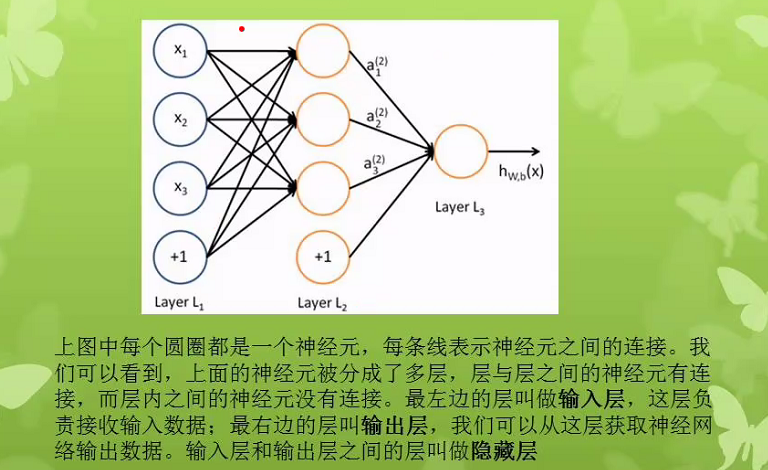
神经网络基本结构

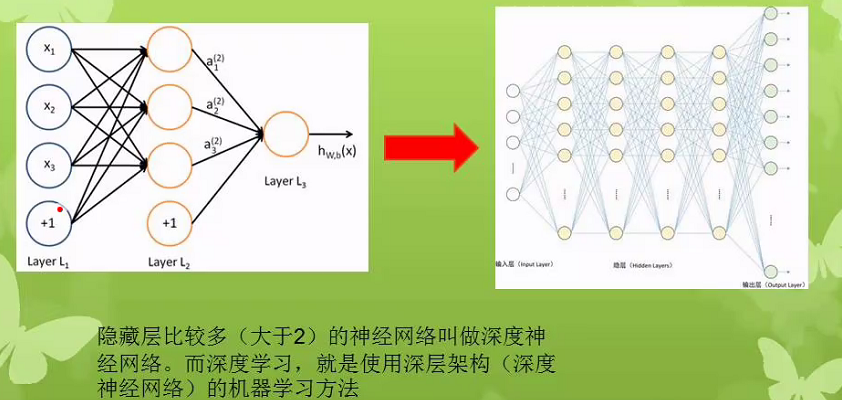
何为深度学习？

二、感知器和激活函数

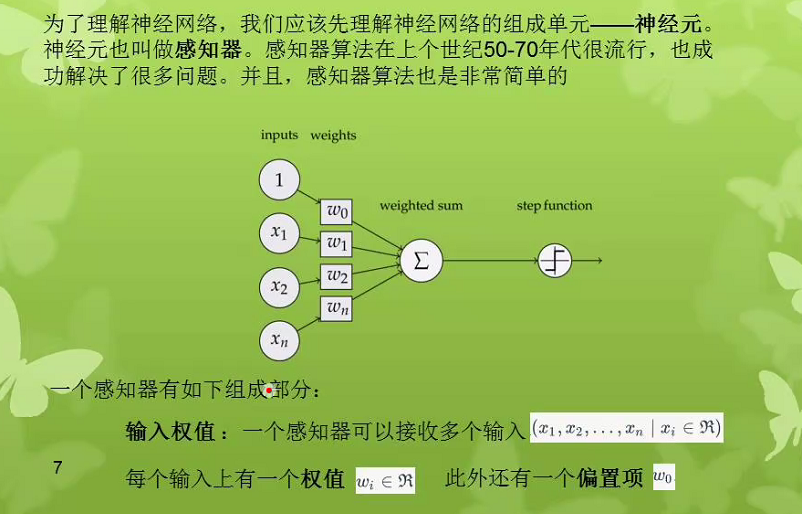
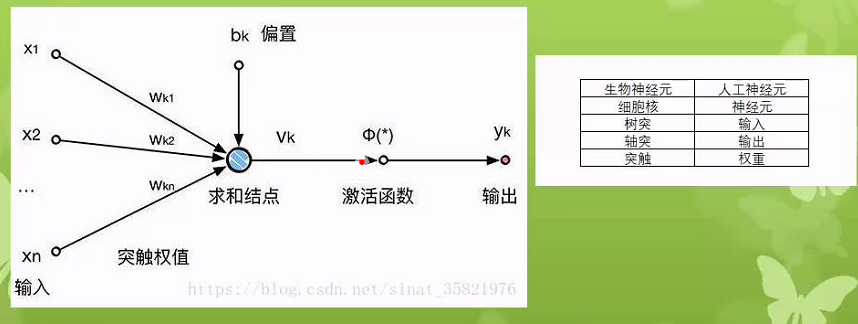
感知器

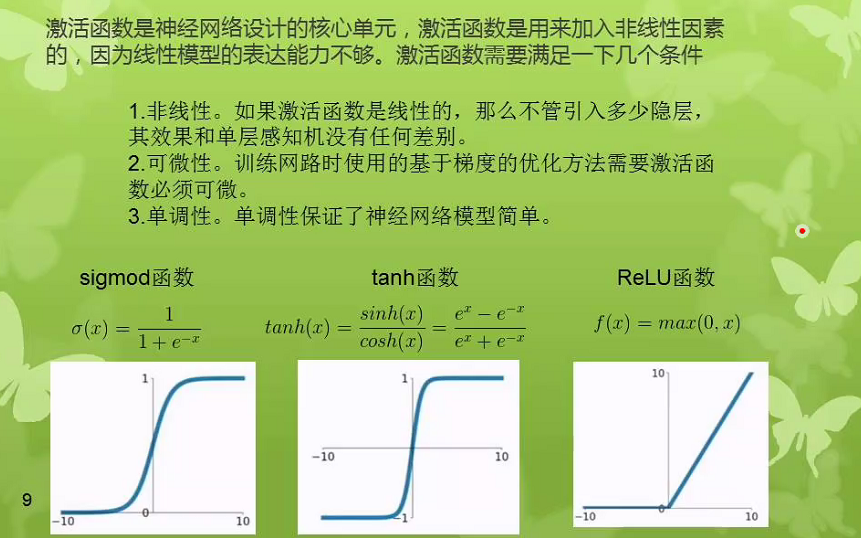
激活函数（其中w和x为向量点乘；b为偏置，w0）

激活函数的选择

三、感知器的训练

四、简单代码实现

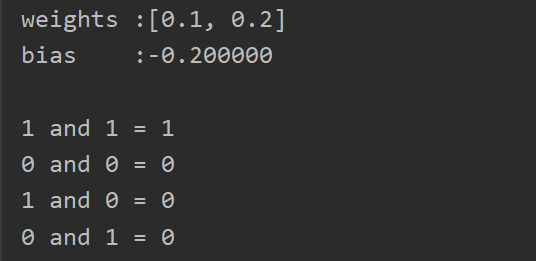
from functools import reduce
class Perceptron(object):
    '''
    构造函数的初始化
    '''
    def __init__(self,input_num,activator):
        '''
        构造函数的初始化
        '''
        self.activator = activator
        self.weights = [0.0 for _ in range(input_num)]
        self.bias = 0.0
    def __str__(self):
        '''
        打印学习后的权重值和偏置项
        '''
        return 'weights\t:%s\nbias\t:%f\n' %(self.weights,self.bias)
    def predict(self,input_vec):
        '''
        输入向量，输出感知器的计算结果
        '''
        return self.activator(
            reduce(lambda a,b: a+b,
                    list(map(lambda x,w: x*w,
                        input_vec,self.weights)
                 ),0.0)+self.bias)
    def train(self,input_vecs,labels,iteration,rate):
        '''
        输入训练数据：一组向量、与每个向量对应的label；以及训练轮数、学习率
        '''
        for i in range(iteration):
            self._one_iteration(input_vecs,labels,rate)
    def _one_iteration(self,input_vecs,labels,rate):
        '''
        迭代，把所有的训练数据过一遍
        '''
        samples = zip(input_vecs,labels)
        for (input_vec,label) in samples:
            output = self.predict(input_vec)
            self._update_weights(input_vec,output,label,rate)
    def _update_weights(self,input_vec,output,label,rate):
        '''
        按照感知器规则更新权重
        '''
        delta = label - output
        self.weights = map(
            lambda x, w:w+rate*delta*x,
            input_vec,self.weights)
        self.weights = list(self.weights)
        self.bias += rate*delta
def f(x):
    '''
    定义激活函数
    '''
    return 1 if x>0 else 0
def get_training_dataset():
    '''
    训练数据
    '''
    input_vecs = [[1,1],[0,0],[1,0],[0,1]]
    labels = [1,0,0,0]
    return input_vecs,labels
def train_and_perceptron():
    '''
    训练感知器
    '''
    p = Perceptron(2,f)
    input_vecs,labels = get_training_dataset()
    p.train(input_vecs,labels,10,0.1)
    return p
if __name__ == '__main__':
    and_perception = train_and_perceptron()
    print(and_perception)
    print('1 and 1 = %d' % and_perception.predict([1,1]))
    print('0 and 0 = %d' % and_perception.predict([0,0]))
    print('1 and 0 = %d' % and_perception.predict([1,0]))
    print('0 and 1 = %d' % and_perception.predict([0,1]))

运行结果：