:::info 贪心算法四个字总结：目前最优 :::

图的一些概念

具体看先前的一篇文章https://www.wztlink1013.com/blog/gqpli5/

连通图

在图论中，连通图基于连通的概念。在一个无向图 G 中，若从顶点i到顶点j有路径相连（当然从j到i也一定有路径），则称i和j是连通的。如果 G 是有向图，那么连接i和j的路径中所有的边都必须同向。如果图中任意两点都是连通的，那么图被称作连通图。如果此图是有向图，则称为强连通图（注意：需要双向都有路径）。图的连通性是图的基本性质。

生成树

包含图的全部顶点，边数最少的连通子图

最小生成树

总权值最小的生成树

常见问题（该算法）就是求最小生成树。
并查集

是一个数据结构，功能有查找a和b是否为同一组；将a和b合并为同一组。

Prim算法思路

Prim——普里姆算法

类似于图的深度优先遍历一样，在遍历到一个结点的时候，在此根据该节点所连通的各边权值，取最小的，以此往复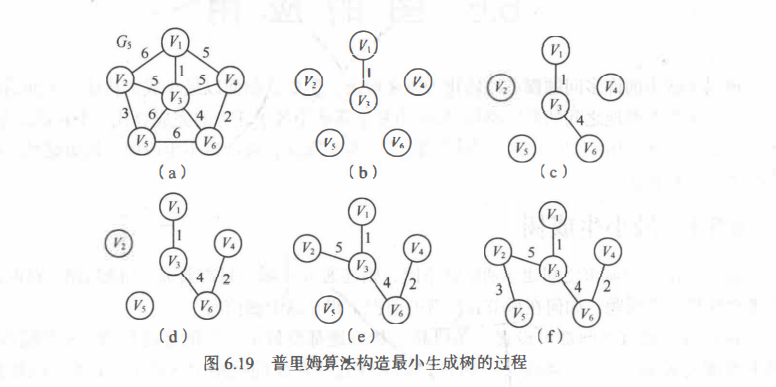
image.png

Kruskal算法思路

Kruskal——克鲁斯卡尔算法

把所有边按照权值全部按数值大小拿出来，然后按顺序选取每条边，利用并查集的思想，如果这条边的两个端点不属于同一集合，那么就将它们合并，直到所有的点都属于同一个集合为止。

比如有如下这么一个图：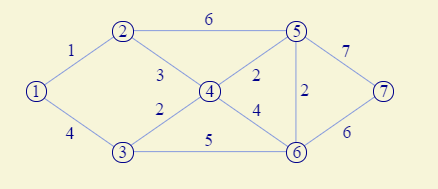
image.png
单独分析①②边和③④边情况下，两个不在一个集合里面，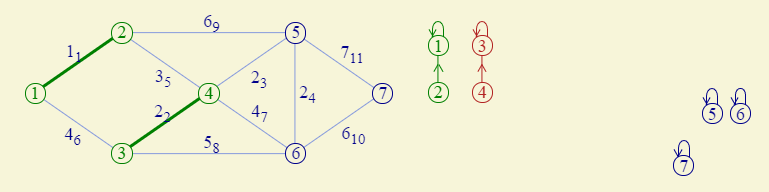
image.png
不断重复，不断判断是否为同一个集合，不在同一个集合的话，就合并，持续如此。比方说当一直操作到权值为3的时候，此时就需要将左右两个集合合并了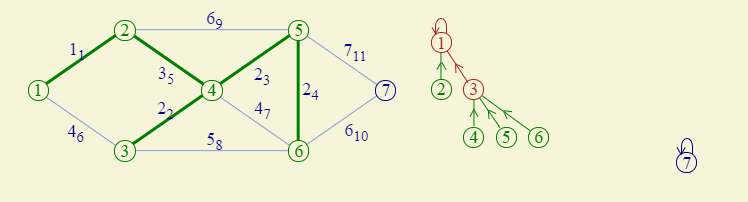
image.png
最后的结果样式就为如下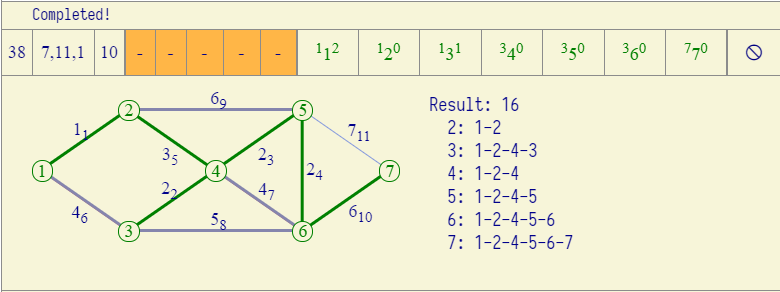
image.png

代码实现

Kruskal算法代码

  1. #include <stdio.h>
  2. #include <vector>
  3. #include <algorithm>
  4. namespace NS_KruskalMST {
  5. using namespace std;
  6. void KruskalMST();
  7. int FindSet(int u);
  8. void UnionSets(int u, int v);
  9. void Initialization();
  10. void GenEdges();
  11. void MakeSets();
  12. void Output(int v0);
  13. #define INF INT_MAX
  14. static int n;
  15. static vector<vector<int>> WMatrix;
  16. static vector<pair<pair<int, int>, int>> Edges;
  17. //Node struct for the disjoint set
  18. struct DJSNode {
  19.     int Parent; int Rank;
  20.     DJSNode(int p) : Parent(p), Rank(0) {}
  21. };
  22. static vector<DJSNode> DisjointSet;
  23. static vector<pair<int, int>> MST;
  24. //The adjacency list for MST
  25. static vector<vector<int>> MSTList;
  26. static vector<int> Prev;
  27. void KruskalMSTCaller(int an, 
  28.     vector<vector<int>> &wMatrix, int v0)
  29. {
  30.     n = an;
  31.     WMatrix = wMatrix;
  32.     Initialization();
  33.     KruskalMST();
  34.     Output(v0);
  35. }
  36. void KruskalMST()
  37. {
  38.     for (auto &e: Edges)
  39.     {
  40.         int u = e.first.first;
  41.         int v = e.first.second;
  42.         int setU = FindSet(u);
  43.         int setV = FindSet(v);
  44.         if (setU != setV)
  45.         {
  46.             MST.push_back(e.first);
  47.             if (MST.size() == n - 1)
  48.                 break;
  49.             UnionSets(setU, setV);
  50.         }
  51.     }
  52. }
  53. int FindSet(int u)
  54. {
  55.     while (u != DisjointSet[u].Parent)
  56.         u = DisjointSet[u].Parent;
  57.         //For path compression:
  58.         //DisjointSet[u].Parent = 
  59.         //    FindSet(DisjointSet[u].Parent);
  60.     return u;
  61. }
  62. void UnionSets(int u, int v)
  63. {
  64.     if (DisjointSet[u].Rank >= DisjointSet[v].Rank)
  65.         DisjointSet[v].Parent = u;
  66.     else
  67.         DisjointSet[u].Parent = v;
  68.     if (DisjointSet[u].Rank == DisjointSet[v].Rank)
  69.         DisjointSet[u].Rank++;
  70. }
  71. void Initialization()
  72. {
  73.     GenEdges();
  74.     sort(Edges.begin(), Edges.end(), 
  75.         [](pair<pair<int, int>, int>a, 
  76.             pair<pair<int, int>, int>b)
  77.         {return a.second < b.second; });
  78.     MakeSets();
  79.     MST.clear();
  80. }
  81. void GenEdges()
  82. {
  83.     Edges.clear();
  84.     //Traverse the upper triangle of WMatrix
  85.     for (int i = 0; i < n - 1; i++)
  86.     {
  87.         for (int j = i + 1; j < n; j++)
  88.             if (WMatrix[i][j] != INF)
  89.                 Edges.push_back({ {i, j},
  90.                     WMatrix[i][j] });
  91.     }
  92. }
  93. void MakeSets()
  94. {
  95.     DisjointSet.clear();
  96.     for (int i = 0; i < n; i++)
  97.         DisjointSet.push_back(DJSNode(i));
  98. }
  99. void OutputWMatrix()
  100. {
  101.     printf("n = %d\n", n);
  102.     printf("The weight matrix:\n");
  103.     printf("%3c", ' ');
  104.     for (int j = 0; j < n; j++)
  105.         printf("%3d", j + 1);
  106.     printf("\n");
  107.     for (int i = 0; i < n; i++)
  108.     {
  109.         printf("%3d", i + 1);
  110.         for (auto j : WMatrix[i])
  111.             if (j < INF)
  112.                 printf("%3d", j);
  113.             else
  114.                 printf("%3c", '*');
  115.         printf("\n");
  116.     }
  117. }
  118. void OutputPath(int u)
  119. {
  120.     if (Prev[u] == -1)
  121.         printf("%d", u + 1);
  122.     else
  123.     {
  124.         OutputPath(Prev[u]);
  125.         printf("-%d", u + 1);
  126.     }
  127. }
  128. void GenMSTList()
  129. {
  130.     MSTList.clear();
  131.     MSTList.resize(n);
  132.     for (auto &e: MST)
  133.     {
  134.         MSTList[e.first].push_back(e.second);
  135.         MSTList[e.second].push_back(e.first);
  136.     }
  137. }
  138. void GenPrev(int v)
  139. {
  140.     for (auto &u : MSTList[v])
  141.         if (u != -1)
  142.         {
  143.             Prev[u] = v;
  144.             auto w = find(MSTList[u].begin(), 
  145.                 MSTList[u].end(), v);
  146.             MSTList[u][w - MSTList[u].begin()] = -1;
  147.             GenPrev(u);
  148.         }
  149. }
  150. void Output(int v0)
  151. {
  152.     printf("Kruskal's MST algorithm\n");
  153.     OutputWMatrix();
  154.     int wSum = 0;
  155.     for (int i = 0; i < n - 1; i++)
  156.         wSum += WMatrix[MST[i].first][MST[i].second];
  157.     GenMSTList();
  158.     Prev.clear();
  159.     Prev.resize(n);
  160.     Prev[v0] = -1;
  161.     GenPrev(v0);
  162.     printf("The MST edges:\n");
  163.     printf("Edge Weight\n");
  164.     for (auto &e : MST)
  165.         printf(" %d-%d  %d\n", e.first + 1, e.second + 1,
  166.             WMatrix[e.first][e.second]);
  167.     printf("Total MST weight: %d\n", wSum);
  168.     printf("The MST paths from vertex %d:\n", v0 + 1);
  169.     for (int u = 0; u < n; u++)
  170.         if (u != v0)
  171.         {
  172.             printf("%3d: ", u + 1);
  173.             OutputPath(u);
  174.             printf("\n");
  175.         }
  176.     printf("\n");
  177. }
  178. } //namespace NS_KruskalMST
  179. using namespace NS_KruskalMST;
  180. void TestKruskalMST(int v0 = 0)
  181. {
  182.     vector<vector<vector<int>>> w = {
  183.         //https://www.geeksforgeeks.org/
  184.         //prims-minimum-spanning-tree-mst-greedy-algo-5/
  185.         {
  186.             {   0,  2,INF,  6,INF },
  187.             {   2,  0,  3,  8,  5 },
  188.             { INF,  3,  0,INF,  7 },
  189.             {   6,  8,INF,  0,  9 },
  190.             { INF,  5,  7,  9,  0 }
  191.         },
  192.         // Dijkstra's algorithm on Wikipedia
  193.         {
  194.             {   0,  7,  9,INF,INF, 14 },
  195.             {   7,  0, 10, 15,INF,INF },
  196.             {   9, 10,  0, 11,INF,  2 },
  197.             { INF, 15, 11,  0,  6,INF },
  198.             { INF,INF,INF,  6,  0,  9 },
  199.             {  14,INF,  2,INF,  9,  0 },
  200.         },
  201.         //https://www.geeksforgeeks.org/
  202.         //kruskals-minimum-spanning-tree-using-stl-in-c/
  203.         {
  204.             {   0,  4,INF,INF,INF,INF,INF,  8,INF },
  205.             {   4,  0,  8,INF,INF,INF,INF, 11,INF },
  206.             { INF,  8,  0,  7,INF,  4,INF,INF,  2 },
  207.             { INF,INF,  7,  0,  9, 14,INF,INF,INF },
  208.             { INF,INF,INF,  9,  0, 10,INF,INF,INF },
  209.             { INF,INF,  4, 14, 10,  0,  2,INF,INF },
  210.             { INF,INF,INF,INF,INF,  2,  0,  1,  6 },
  211.             {   8, 11,INF,INF,INF,INF,  1,  0,  7 },
  212.             { INF,INF,  2,INF,INF,INF,  6,  7,  0 },
  213.         },
  214.     };
  215.     int k = w.size();
  216.     for (int i = 0; i < k; i++)
  217.     {
  218.       if (v0 > w[i].size() - 1)
  219.         v0 = w[i].size() - 1;
  220.       KruskalMSTCaller(w[i].size(), w[i], v0);
  221.     }
  222. }