备查附录

代数

几何

点到直线距离公式：

自然底数

要了解 的由来，一个最直观的方法是引入一个经济学名称“复利(Compound Interest)” — 复利率法（英文：compound interest），是一种计算利息的方法。按照这种方法，利息除了会根据本金计算外，新得到的利息同样可以生息，因此俗称“利滚利”、“驴打滚”或“利叠利”。只要计算利息的周期越密，财富增长越快，而随着年期越长，复利效应亦会越为明显。

我们知道，很多细菌是通过二分裂进行繁殖的，假设某种细菌天会分裂次，也就是个增长周期为天，这意味着：每一天，细菌的总数量都是前一天的两倍。显然，如果经过天（或者说，经过个增长周期）的分裂，就相当于翻了倍。即，在第天时，细菌总数将是初始数量的倍。

如果假设初始数量为，那么天后的细菌数量则为。因此，只要保证所有细菌天分裂次，不管初始数量是多少，最终数量都将是初始数量的倍。因此，此计算关系也可以写为：

如果将 “分裂”或“翻倍”换一种更文艺的说法，也可以说是：“增长率为”。也就是说，可以将上式写为：

而当增长率不是，而是、之类的时候，则只需要将上式的换成想要的增长率即可。这样就可以得到更加普适的公式：

这个公式的数学内涵是：一个增长周期内的增长率为，在增长了个周期之后，总数量将为初始数量的倍。以上为指数增长的一个简单实例，下面来看看雅可比·伯努利的发现：

假设你有元钱存在银行里，此时发生了严重的通货膨胀，银行的利率飙到了（夸张一下，为了方便计算）。如果银行一年付一次利息，自然在一年后你可以拿到元的本金（蓝色圆）和元的利息（绿色圆），总共两元的余额。

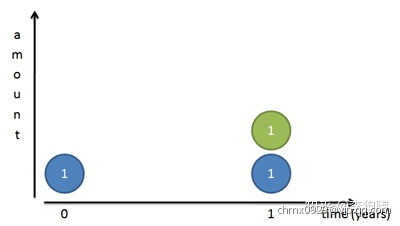
现在银行的年利率不变，但银行为了招揽客户，推出一项惠民政策，每半年就付一次利息。那么到第六个月（也就是半年）的时候，你就能够提前从银行拿到元的利息了。

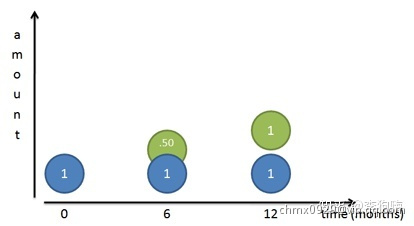
机智的你会马上把这元的利息再次存入银行，这元的利息也将在下一结算周期产生利息(红色圆)，专业术语叫“复利”，那么年底的存款余额将等于元。

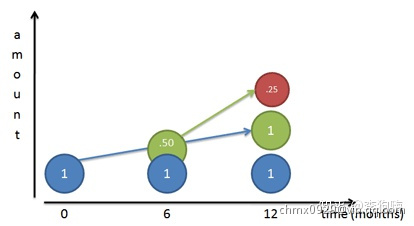
此时，我们可以换个角度这样看：即，每个结算（增长）周期为半年，每半年的利率是（或者说），一年结算两次利息，且第一次结算完后，立马将利息存入。此时我们的计算公式和结果如下：

继续，假设现在银行为了和其他银行抢生意，短期不想赚钱了，每四个月就付一次利息！而机智的你依然一拿到利息就立马存入，与半年结算一次利息类似：即，每个结算周期为四个月，每四个月的利率是（或者说 ），一年结算三次利息，且前两次结算完后，都立马将所有利息存入。

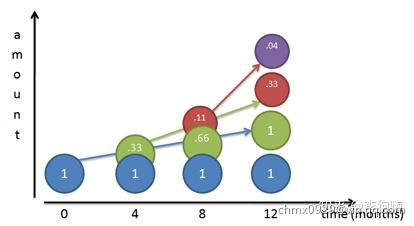
此时计算公式和结果如下：

我的天，年利率虽然没有变，但随着每年利息交付次数的增加，你年底能从银行拿到的钱居然也在增加！那么是不是会一直增大到无穷大呢？想得倒美…

现在假设存款人和银行都疯了，银行在保证年利率为的前提下连续不断地付给存款人利息，存款人天天呆在银行不走，拿到利息就往银行里存。这样，所得利息即所谓“连续复利”。

但是，你会发现，似乎有一个“天花板”挡住了你企图靠块钱疯狂赚取个亿的小目标，这个“天花板”就是！如果，我们进行一系列的迭代运算，我们将看到以下结果：

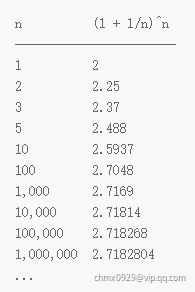
其中，指的是一年中结算利息的次数。只要在年利率保持不变的情况下，不断地提高利息的结算次数，余额就将会逼近

然后，终于可以祭出这个高等数学微积分里计算 的一个重要极限了：

现在再回头看这个重要极限，想必会有更加直观的理解。

大数定律

小数定律

喜欢总结规律是人类的天性。例如，人们抱着娱乐或者认真的态度总结了世界杯足球赛的各种“定律”，其中比较著名的有“巴西队的礼物”——“巴西队的礼物”是指：只要巴西夺冠，下一届的冠军就将是主办大赛的东道主，除非是巴西队自己夺冠。我们来看下历史下真实的数据：1962年巴西夺冠后，4年后英格兰在本土称雄。1970年巴西三夺金杯，1974年轮到东道主西德捧杯。1994年巴西在美国夺冠，下一届东道主法国队在本土夺冠。1958年，巴西队在瑞典夺冠，4年后他们未免成功，收回了“礼物”。看起来这个定律很有意思，但是这一定律在2006年被打破。2006年在德国的世界杯，德国和巴西队都没有夺冠，而是由我们中国人耳熟能详的主队里皮率领的意大利队夺冠。还有一些未被打破的定律，这些看似没有规律的神奇定律，之所有神奇，完全纯属巧合。世界杯每4年举办一次，总共才举办了20多届。只要数据足够少，我们总能发现一些神奇的定律。

如果数据少，随机现象可以看起来很不随机。甚至非常整齐，好像真的有规律一样。即小数定律——如果统计数据很少，那么事件就表现为各种极端情况，而这些情况都是偶然事件，跟它的期望值一点关系也没有

大数定律

大数定律就是我们从统计学中推测真相的理论基础——大数定律说如果统计数据足够大，那么事物出现的频率就能无限接近它的期望值。

某个事件的期望，也就是收益，实际上各种不同结果出现的概率乘结果的收益的和。拿我们最熟悉的投骰子举例，游戏规则是投中1点获得1元，投中2点获得2元，以此类推。那么，这个事件的期望是多少呢？

显然是

这个期望3.5代表什么意思呢？也就是说，只要你一直玩下去，你每次游戏的预期收益是3.5元。可能你某次赢了1元，某一次赢了6元，只要你长期投下去， 你平均下来每次就赢3.5元。

中心极限定理

中心极限定理是许多统计活动的“动力源泉”，这些活动存在着一个共同的特点，那就是使用样本对总体进行估计，例如我们经常看到的民意调查就是这方面的经典案例。

中心极限定理是说：

• 样本的平均值约等于总体的平均值。
• 不管总体是什么分布，任意一个总体的样本平均值都会围绕在总体的整体平均值周围，并且呈正态分布。

假设有一个群体，如我们之前提到的清华毕业的人，我们对这类人群的收入感兴趣。怎么知道这群人的收入呢？我会做这样4步：

1. 随机抽取1个样本，求该样本的平均值。例如我们抽取了100名毕业于清华的人，然后对这些人的收入求平均值。该样本里的100名清华的人，这里的100就是该样本的大小。有一个经验是，样本大小必须达到30，中心极限定理才能保证成立。
2. 我将第1步样本抽取的工作重复再三，不断地从毕业的人中随机抽取100个人，例如我抽取了5个样本，并计算出每个样本的平均值，那么5个样本，就会有5个平均值。这里的5个样本，就是指样本数量是5，即抽取了5次，形成了5个样本。
3. 根据中心极限定理，这些样本平均值中的绝大部分都极为接近总体的平均收入。有一些会稍高一点，有一些会稍低一点，只有极少数的样本平均值大大高于或低于群体平均值。
4. 中心极限定理告诉我们，不论所研究的群体是怎样分布的，这些样本平均值会在总体平均值周围呈现一个正态分布。

Source

https://zhuanlan.zhihu.com/p/48391055
https://blog.csdn.net/anshuai_aw1/article/details/82771784
https://blog.csdn.net/anshuai_aw1/article/details/82769742