">
Py成功不是比别人优秀多少， 二十比昨天的自己进步多少？
https://www.lanqiao.cn/courses/2616/learning/?id=45501
https://www.lanqiao.cn/courses/2616
第一章 PyTorch 使用简介
一、实验介绍
1.1 实验内容
Pytorch 是由 Facebook 支持的一套深度学习开源框架，
相比较 Tensorflow，它更加容易快速上手，所以一经推出就广受欢迎。
本课程是采用 Pytorch 开源框架进行案例讲解的深度学习课程。
Tensor（张量）是 PyTorch 的基础数据结构，自动微分运算是深度学习的核心。
在本实验中我们将学习 PyTorch 中 Tensor 的用法，以及简单的自动微分变量原理，
最后，我们还会使用 PyTorch 构建一个简单的线性回归网络。
1.2 实验知识点
- PyTorch 简介
- PyTorch 中的张量及其运算
- PyTorch 中的自动微分运算
-
1.3 实验环境
Python 3.6
- PyTorch 1.0.1
- Jupyter Notebook
1.4 适合人群
本课程难度为一般，属于初级实践级别课程，适合具有 Python 基础并对深度学习有一定认识的用户，将 PyTorch 应用到简单问题的解决
1.5 索引目录¶
一、实验介绍
二、有关张量（Tensor）运算的练习
三、有关自动微分（Autograd）变量的练习
四、利用PyTorch实现简单的线性回归算法
二、有关张量（Tensor）运算的练习
2.1 使用 Tensor
PyTorch 是一个开源的深度学习框架，由 Facebook 支持开发。
它的前身为 Torch，但因为 Torch 使用的编程语言是 Lua，在国内流行度很小。
Facebook 为了迎合数量更多的 Python 用户的需求，推出了 PyTorch。
PyTorch 完全开源意味着你可以轻易获取它的代码，并按照自己的需求对它进行修改。
比如让 PyTorch 支持复数运算等等。
PyTorch 还有另外一个非常出众的特点是，
使用 PyTorch 框架编写出的神经网络模型的代码非常简洁。
实现同样的功能，使用 PyTorch 框架编写的代码往往更清晰明了，
这点我们可以从下图中略见一斑：
PyTorch 的基本数据单元是张量（Tensor），它实际上是一种 N 维数组。
下面我们列举了三种张量，可以看到它们的维度阶数是不同的。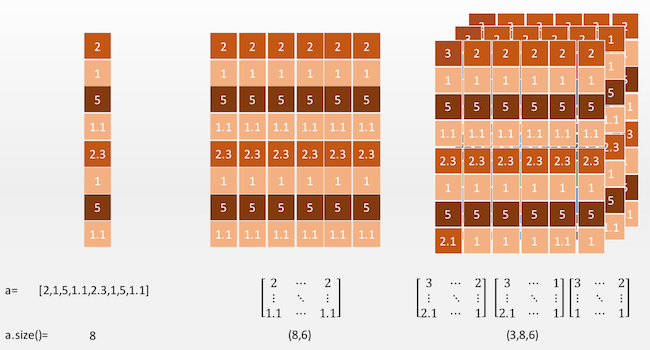
1 阶的张量可以看做是一个向量，通过索引可以取到一个“值”。
2 阶张量可以看做为一个矩阵，通过索引可以取到一个个的向量。
3 阶张量有点抽象，不过我们可以从图中看出，
3 阶张量其实就是在 2 阶张量的矩阵中增加了一个深度。
也就是说在 3 阶张量中我们可以通过索引取到一个个的矩阵。
我们不难想象，4 阶张量也就是在 3 阶张量上增加了另外一个轴……
我们可以使用 Tensor.size() 方法获得一个张量的“尺寸”。
在这里注意“尺寸”和维度是两个概念。
就比如对于上图中的 1 阶张量，它的维度为 1，尺寸为 8；
对于上图中的 2 阶张量，它的维度为 2，尺寸为（8，6）。
要使用 PyTorch，首先需要在 Python 中引入 PyTorch 的包。
▶ 示例代码：
import torch #导入torch包
可以通过以下代码查看当前系统中 PyTorch 的版本：
▶ 示例代码：
print(torch.version)
可以生成随机数张量：
▶ 示例代码：
x = torch.rand(5, 3) #产生一个53的tensor，随机取值 x #显示x的值
可以使用 zeros，ones 方法生成包含固定值的张量：
▶ 示例代码：
y = torch.ones(5, 3) #产生一个53的Tensor，元素都是1 y
2.2 基本 Tensor 运算
两个 2 阶张量相加的方法实际上就是矩阵加法。
注意，要使两个张量相加，必须保证两个张量的尺寸是一致的。
▶ 示例代码：
z = x + y #两个tensor可以直接相加 z
下面的语句展示了两个 tensor 按照矩阵的方式相乘，注意 x 的尺寸是 53，
y 的尺寸也是 53 无法进行矩阵乘法，所以先将 y 进行转置。
转置操作可以用 .t() 来完成，也可以用 transpose(0, 1) 来完成。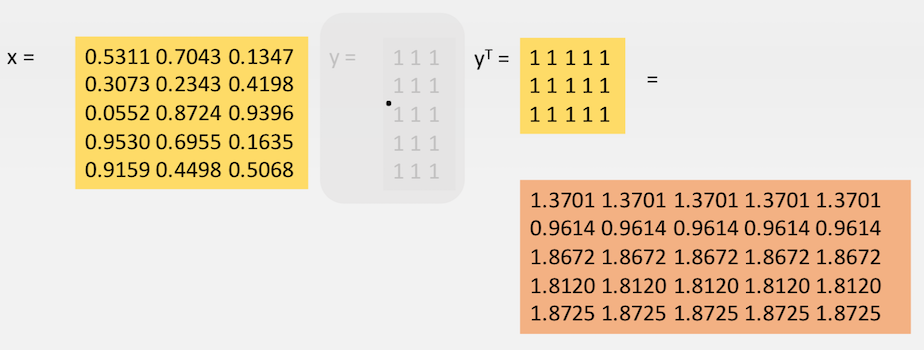
▶ 示例代码：
q = x.mm(y.t()) #x乘以y的转置 q
所有的Tensor的使用方法请见参考链接中的“Tensor支持的所有操作”。
2.3 Tensor 与 numpy.ndarray 之间的转换
PyTorch 的 Tensor 可以与 Python 的常用数据处理包 Numpy 中的多维数组进行转换。
▶ 示例代码：
import numpy as np #导入numpy包
a = np.ones([5, 3]) #建立一个53全是1的二维数组（矩阵）
b = torch.from_numpy(a) #利用from_numpy将其转换为tensor
b
下面是另外一种转换 Tensor 的方法，类型为 FloatTensor。
▶ 示例代码：
# 还可以是LongTensor，整型数据类型
c = torch.FloatTensor(a)
c
还可以从一个 tensor 转化为 numpy 的多维数组
*▶ 示例代码：
b.numpy()
Tensor 和 Numpy 的最大区别在于 Tensor 可以在 GPU 上进行运算。
默认情况下，Tensor 是在 CPU 上进行运算的，
如果我们需要一个 Tensor 在 GPU 上的实例，需要运行这个 Tensor 的 .cuda() 方法。
在下面的代码中，首先判断在本机上是否有 GPU 环境可用（有 NVIDIA的 GPU，并安装了驱动）。
如果有 GPU 环境可用，那么再去获得张量 x，y 的 GPU 实例。
注意在最后打印 x 和 y 这两个 GPU 张量的和的时候，我们调用了 .cpu() 方法，
意思是将 GPU 张量转化为 CPU 张量，否则系统会报错。
▶ 示例代码：
if torch.cuda.is_available(): #检测本机器上有无GPU可用x = x.cuda() #返回x的GPU上运算的版本y = y.cuda()z = x + yprint(z.cpu()) # 打印时注意要把GPU变量转化为CPU变量。
三、有关自动微分（Autograd）变量的练习
3 基本概念
3.1 反向传播算法
https://www.cnblogs.com/wlzy/p/7751297.html
反向传播算法（Backpropagation）是目前用来训练人工神经网络（Artificial Neural Network，ANN）的最常用且最有效的算法。其主要思想是：
（1）将训练集数据输入到ANN的输入层，经过隐藏层，最后达到输出层并输出结果，这是ANN的前向传播过程；
（2）由于ANN的输出结果与实际结果有误差，则计算估计值与实际值之间的误差，并将该误差从输出层向隐藏层反向传播，直至传播到输入层；
（3）在反向传播的过程中，根据误差调整各种参数的值；不断迭代上述过程，直至收敛。
反向传播算法的思想比较容易理解，但具体的公式则要一步步推导，因此本文着重介绍公式的推导过程。
3.2 反向传播算法伪代码
- 输入训练集
- 对于训练集中的每个样本x，设置输入层（Input layer）对应的激活值
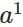：- 前向传播：
， 
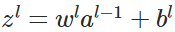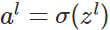
- 计算输出层产生的错误：
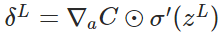
- 反向传播错误：
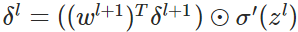
- 使用梯度下降（gradient descent），训练参数：
3.3 变量定义
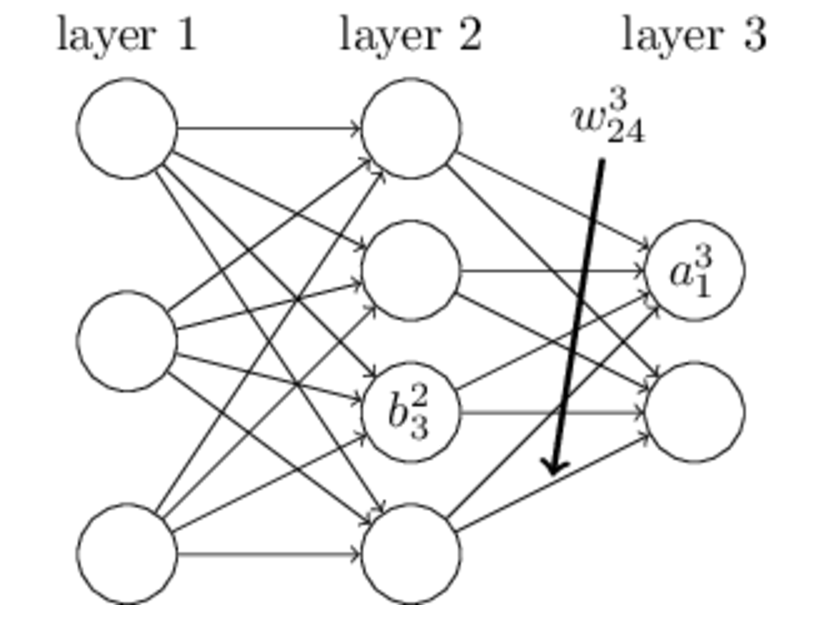
上图是一个三层人工神经网络，layer1至layer3分别是输入层、隐藏层和输出层。如图，先定义一些变量：
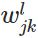表示第
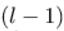层的第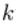
个神经元连接到第
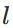层的第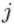
个神经元的权重；
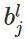表示第
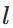层的第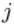
个神经元的偏置；
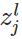表示第
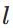层的第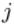
个神经元的输入，即：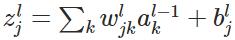
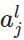表示第
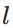层的第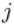
个神经元的输出，即：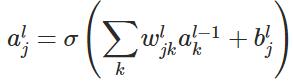
其中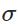
表示激活函数。
3.4 代价函数
代价函数被用来计算ANN输出值与实际值之间的误差。常用的代价函数是二次代价函数（Quadratic cost function）：<br />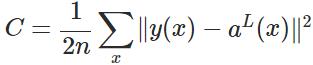<br /> 其中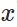，表示输入的样本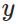，表示实际的分类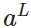，表示预测的输出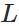，表示神经网络的最大层数。<br />
3.5 公式及其推导
本节将介绍反向传播算法用到的4个公式，并进行推导。**如果不想了解公式推导过程，请直接看第4节的算法步骤。**<br /> 首先，将第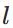层第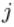个神经元中产生的错误（即实际值与预测值之间的误差）定义为：<br />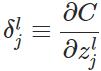<br /> <br /> <br /> 本文将以一个输入样本为例进行说明，此时代价函数表示为：<br />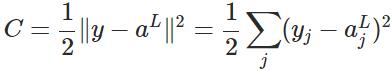<br /> <br />**公式1（计算最后一层神经网络产生的错误）：**<br />** **<br />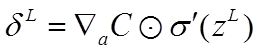<br /> <br /> 其中，表示Hadamard乘积，用于矩阵或向量之间点对点的乘法运算。公式1的推导过程如下：<br />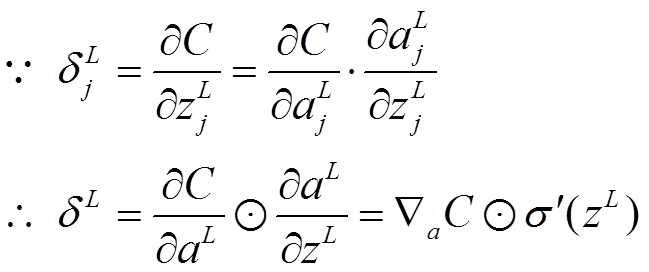<br /> <br /> <br />**公式2（由后往前，计算每一层神经网络产生的错误）：**<br />** **<br />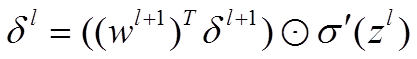<br /> <br /> 推导过程：<br />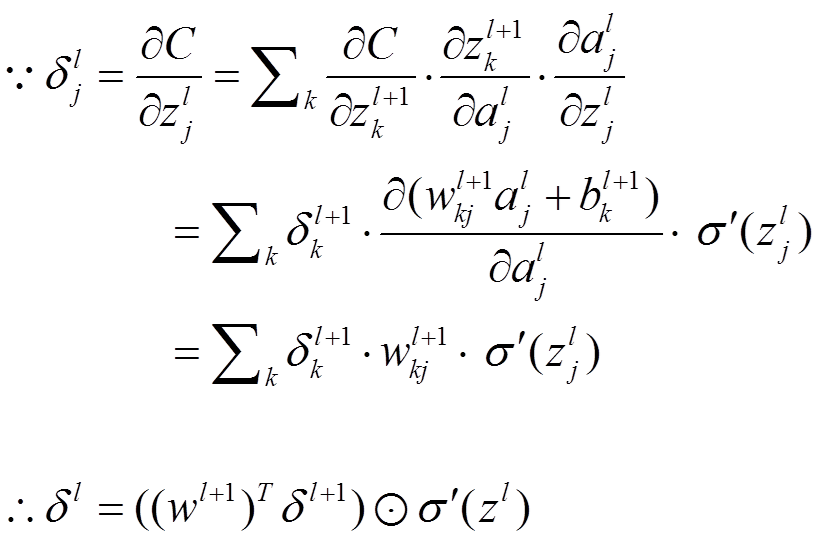<br /> <br /> <br />**公式3（计算权重的梯度）：**<br />** **<br />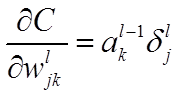<br /> <br /> 推导过程：<br />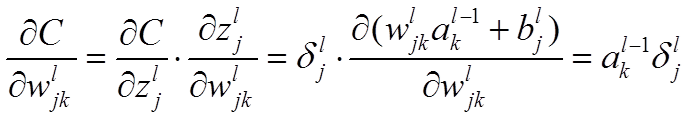<br /> <br /> <br />**公式4（计算偏置的梯度）：**<br />** **<br />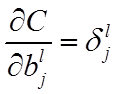<br /> <br /> 推导过程：<br />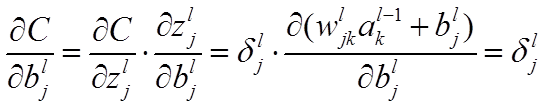<br /> <br />
动态运算图(Dynamic Computation Graph)是 PyTorch 的最主要特性，
它可以让我们的计算模型更灵活、复杂，并可以让反向传播算法随时进行。
而反向传播算法就是深度神经网络的核心。
下面是一个计算图的结构以及与它对应的 PyTorch 代码：
用来构建计算图的数据叫做自动微分变量（Variable），它与 Tensor 不同。
每个 Variable 包含三个属性，分别对应着数据（data），父节点（creator），以及梯度（grad）。
其中“梯度”就是反向传播算法所要传播的信息。
而父节点用于将每个节点连接起来构建计算图（如上图所示）。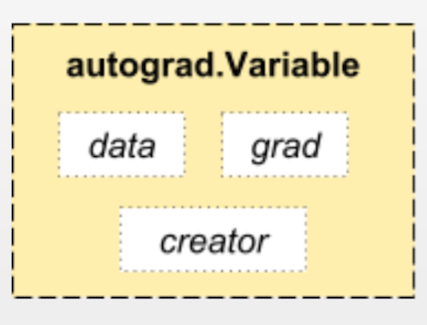
下面我们编写代码实际使用自动微分变量。
▶ 示例代码：
#导入自动梯度的运算包，主要用Variable这个类from torch.autograd import Variable#创建一个Variable，包裹了一个2*2张量，将需要计算梯度属性置为Truex = Variable(torch.ones(2, 2), requires_grad=True)x
可以按照 Tensor 的方式进行计算
▶ 示例代码：
y = x + 2 #可以按照Tensor的方式进行计算y.grad_fn #每个Variable都有一个creator（创造者节点）
经过上面变量 x 和 y 的运算，我们就有了一个简单的计算图，它是下面这个样子的：
叶子节点：指向位置X
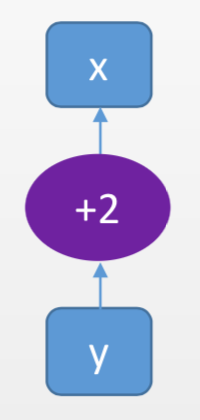
下面我们让计算图再复杂一点，我们再加入变量 z:
注意，.data 可以返回一个 Variable 所包裹的 Tensor
▶ 示例代码：
z = torch.mean(y y) #也可以进行复合运算，比如求均值mean
z.data #.data属性可以返回z所包裹的tensor
现在我们的计算图是这个样子的：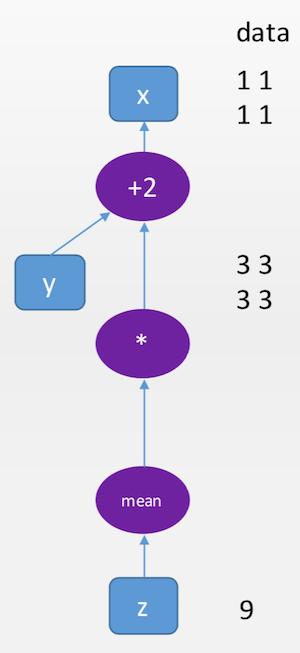
backward 可以实施反向传播算法，并计算所有计算图上叶子节点（没有子节点）的导数（梯度）信息。
注意，由于 z 和 y 都不是叶子节点，所以都没有梯度信息
▶ 示例代码：
z.backward() #梯度反向传播
print(z.grad) # 无梯度信息
print(y.grad) # 无梯度信息
print(x.grad)
在下面的例子中，会让矩阵 x 反复作用在向量 s 上，系统会自动记录中间的依赖关系和长路径。
▶ 示例代码：
s = Variable(torch.FloatTensor([[0.01, 0.02]]), requires_grad = True)
#创建一个12的Variable（1维向量）
x = Variable(torch.ones(2, 2), requires_grad = True) #创建一个22的矩阵型Variable
for i in range(10):
s = s.mm(x) #反复用s乘以x（矩阵乘法），注意s始终是12的Variable
z = torch.mean(s) #对s中的各个元素求均值，得到一个11的scalar（标量，即11张量）
然后我们得到了一个复杂的“深度”计算图：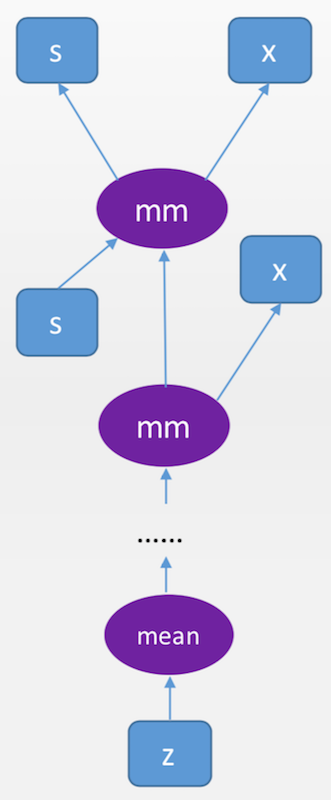
▶ 示例代码：
z.backward() #在具有很长的依赖路径的计算图上用反向传播算法计算叶节点的梯度
print(x.grad) #x作为叶节点可以获得这部分梯度信息
print(s.grad) #s不是叶节点，没有梯度信息
如果大家觉得去理解这个计算图的叶子结点很困难，这也没有关系。
因为我们研究的主题是深度学习，PyTorch 框架会自动搭建好计算图的。
回到目录
四、利用PyTorch实现简单的线性回归算法
4.1 准备数据
下面使用 PyTorch 实现一个简单的线性回归算法。
线性回归是机器学习中最基础和简单的算法，你可以将它视为深度学习界的 Hello World。
如果不了解线性回归，你可以简单的理解为：训练一条直线，让这条直线拟合一些数据点的趋势。
大部分的同学在高中或者大学肯定接触过线性回归，所以我在这里也不做过多的介绍了。
首先生成一些样本点作为原始数据。
这些原始“数据点”就是直线需要拟合的对象。
▶ 示例代码：
# linspace可以生成0-100之间的均匀的100个数字x = Variable(torch.linspace(0, 100).type(torch.FloatTensor))# 随机生成100个满足标准正态分布的随机数，均值为0，方差为1.# 将这个数字乘以10，标准方差变为10rand = Variable(torch.randn(100)) * 10# 将x和rand相加，得到伪造的标签数据y。# 所以(x,y)应能近似地落在y=x这条直线上y = x + rand
将生成的原始数据点画在图上，用视觉观察下数据点的“趋势”。
▶ 示例代码：
import matplotlib.pyplot as plt #导入画图的程序包%matplotlib inlineplt.figure(figsize=(10,8)) #设定绘制窗口大小为10*8 inch# 绘制数据，考虑到x和y都是Variable，# 需要用data获取它们包裹的Tensor，并专成numpyplt.plot(x.data.numpy(), y.data.numpy(), 'o')plt.xlabel('X') #添加X轴的标注plt.ylabel('Y') #添加Y轴的标注plt.show() #将图形画在下面
所有的数据点以视觉可见的增势增长。下面我们构造模型，来拟合这些数据点。
4.2 构造模型 计算损失函数
我们要使用一条直线去拟合若干个点的走势，那在数学上怎么表示这条直线哪？
这个大家在高中应该都学过，可以用 ax+b 来表示一条直线。
因为这条直线是由参数 a 和 b 控制的，所以模型就是要“学习”出这两个参数。
那么下面首先建立变量，随机初始化用于线性拟合的参数 a 和 b。
▶ 示例代码：
#创建a变量，并随机赋值初始化a = Variable(torch.rand(1), requires_grad = True)#创建b变量，并随机赋值初始化b = Variable(torch.rand(1), requires_grad = True)print('Initial parameters:', [a, b])
在当前的模型中，这两个参数的初始值无关紧要，因为下面会通过 1000 次的训练，来反复修正这两个参数。
在下面的代码中，需要注意 expandas 和 mul 的使用。
首先，a 的维度为 1，x 是维度为 1001 的 Tensor，这两者不能直接相乘，因为维度不同。
所以，先要将 a 升维成 11 的 Tensor。
这就好比将原本在直线上的点被升维到了二维平面上，同时直线仍然在二维平面中。
expand_as(x) 可以将张量升维成与 x 同维度的张量。所以如果 a = 1, x 为尺寸为 100，
那么，a.expand_as(x)= (1, 1, \cdot\cdot\cdot, 1)^T=(1,1,⋅⋅⋅,1)_T
x y 为两个 1 维张量的乘积，计算结果：
(x y)i = x_i \cdot y_i(_x∗y)i=xi⋅yi
▶ 示例代码：
learning_rate = 0.0001 #设置学习率for i in range(1000):### 下面这三行代码非常重要，这部分代码，清空存储在变量a，b中的梯度信息，### 以免在backward的过程中会反复不停地累加#如果a和b的梯度都不是空if (a.grad is not None) and (b.grad is not None):a.grad.data.zero_() #清空a的数值b.grad.data.zero_() #清空b的数值#计算在当前a、b条件下的模型预测数值predictions = a.expand_as(x) * x + b.expand_as(x)#通过与标签数据y比较，计算误差loss = torch.mean((predictions - y) ** 2)print('loss:', loss.data.numpy())loss.backward() #对损失函数进行梯度反传#利用上一步计算中得到的a的梯度信息更新a中的data数值a.data.add_(- learning_rate * a.grad.data)#利用上一步计算中得到的b的梯度信息更新b中的data数值b.data.add_(- learning_rate * b.grad.data)
从打印出的损失中我们可以观察到损失一直在下降。
我们现在可以把直线绘制出来，看看这条直线是什么样子。
▶ 示例代码：
x_data = x.data.numpy() # 获得x包裹的数据plt.figure(figsize = (10, 7)) #设定绘图窗口大小xplot, = plt.plot(x_data, y.data.numpy(), 'o') # 绘制原始数据yplot, = plt.plot(x_data, a.data.numpy() * x_data + b.data.numpy()) #绘制拟合数据plt.xlabel('X') #更改坐标轴标注plt.ylabel('Y') #更改坐标轴标注str1 = str(a.data.numpy()[0]) + 'x +' + str(b.data.numpy()[0]) #图例信息plt.legend([xplot, yplot],['Data', str1]) #绘制图例plt.show()
可以观察到直线已经拟合了点的走势。
你可以修改训练次数，把训练次数改的很小，或者增加 10 倍，看看线性拟合会有什么变化。
4.3 测试模型
虽然模型很简单，但我们仍要进行测试的流程。
因为“准备数据”、“模型设计”、“训练”、“测试”是完成深度学习任务的基本套路。
▶ 示例代码：
x_test = Variable(torch.FloatTensor([1, 2, 10, 100, 1000])) #随便选择一些点1，2，……，1000predictions = a.expand_as(x_test) * x_test + b.expand_as(x_test) #计算模型的预测结果predictions #输出
4.4模型的保存和加载
Python中对于模型数据的保存和加载操作都是引用Python内置的pickle包，使用pickle.dump()和pickle.load()方法。在PyTorch中也有同样功能的方法提供。
>>> torch.save(model,'model.pkl') # 保存整个模型>>> model = torch.load('model.pkl') #加载整个模型>>> torch.save(alexnet.state_dict(),'params.pkl') # 保存网络中的参数>>> alexnet.load_state_dict(torch.load('params.pkl')) # 加载网络中的参数
五、实验总结
在本节实验中，我们熟悉了张量、自动微分变量的用法，认识了PyTorch中的计算图，并动手实践完成了一个线性回归模型。如果你亲自动手实践了每一行代码，我相信你对PyTorch的基本用法一定有了些许了解。在本节实验中积累的经验非常重要，因为你在以后的实验中会一直用到今天学习的知识点。
六、参考链接
Tensor 支持的所有操作：
http://pytorch.org/docs/0.3.0/tensors.html
第二章 预测共享单车的使用量
一、实验介绍
1.1 实验内容
在本次实验中，我们将设计我们的第一个有实用价值的人工神经网络，并用它来预测未来某地区租赁单车的使用情况。
1.2 实验知识点
- 数据归一化、类型变量的转换
- 搭建基本神经网络的方法
- 数据分批次训练原则
- 测试及简单分析神经网络的方法
1.3 实验环境
- Jupyter Notebook
- Python 3.6
- PyTorch 1.0.1
1.4 适合人群
本课程难度为一般，属于深度学习初级实践级别课程，适合初学深度学习，对深度神经网络、反向传播、梯度下降等概念有一定认识的同学。
1.5 索引目录
一、实验介绍
二、预处理实验数据
三、构建神经网络模型
四、测试网络
二、预处理实验数据
2.1 读取数据
首先假设我们是某家共享单车企业的合作伙伴，现在拥有这家公司两年内共享单车的使用数据。
那么问题来了，我们的客户，也就是这家共享单车公司，要求我们根据过去两年的单车使用数据训练一个模型出来，用于预测单车在未来的使用量。
我该怎么做哪？别慌，在建立模型前，先观察一下这两年间共享单车使用情况的数据。
In [ ]:
# 下载并解压数据集
!wget http://labfile.oss.aliyuncs.com/courses/1073/bike-sharing-dataset.zip
!unzip bike-sharing-dataset.zip
▶ 示例代码：
In [ ]:
#导入需要使用的库import numpy as npimport pandas as pd #读取csv文件的库import matplotlib.pyplot as pltimport torchfrom torch.autograd import Variableimport torch.optim as optim# 让输出的图形直接在Notebook中显示%matplotlib inline
记录共享单车使用情况的数据都在文件“hour.csv”中，该文件大小为 1.2M，完全可以直接读取到内存中。
下面读取这个文件，并运用 pandas 模块的 head 方法，将数据的数据表头和部分数据项打印出来。
▶ 示例代码：
In [ ]:
#首先，让我们再来看看数据长什么样子#读取数据到内存中，rides为一个dataframe对象data_path = 'bike-sharing-dataset/hour.csv'rides = pd.read_csv(data_path)rides.head()
可以观察到，数据文件记录了每小时（hr）共享单车的使用数量（cnt），
除了这两个数据项外，还包括当天的日期（dteday），季节（season），星期几（weekday），是否是假期（holiday），
当天的温度、湿度、风速、用户是否注册等等，我们就是要使用这些数据训练神经网络模型。
2.2. 对于类型变量的处理
数据文件中的数据往往不能直接用来训练神经网络模型。
因为这些数据具有不同的数据类型，不同的取值范围，
在将它们用在神经网络模型中之前，要对这些数据进行一系列的预处理。
首先是类型变量。
类型变量是指这个变量的不同值仅仅表达不同的类型，值的大小不同但没有高低之分。
有很多变量都属于类型变量，例如 season=1,2,3,4 代表四季。
我们不能将 season 变量直接输入到神经网络，这是因为 season 数值越高并不表示相应的信号强度越大。
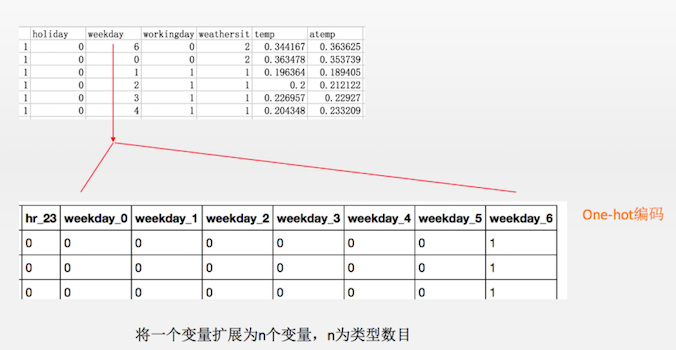
解决方案是将类型变量用一个“一位热码“（one-hot）来编码，也就是：
𝑠𝑒𝑎𝑠𝑜𝑛=1→(1,0,0,0)𝑠𝑒𝑎𝑠𝑜𝑛=2→(0,1,0,0)𝑠𝑒𝑎𝑠𝑜𝑛=3→(0,0,1,0)𝑠𝑒𝑎𝑠𝑜𝑛=4→(0,0,0,1)season=1→(1,0,0,0)season=2→(0,1,0,0)season=3→(0,0,1,0)season=4→(0,0,0,1)
因此，如果一个类型变量有 n 个不同取值，那么我 one-hot 所对应的向量长度就为 n。
▶ 示例代码：
In [ ]:
#对于类型变量的特殊处理
# season=1,2,3,4, weathersi=1,2,3, mnth= 1,2,…,12, hr=0,1, …,23, weekday=0,1,…,6
# 经过下面的处理后，将会多出若干特征，例如，对于season变量就会有 season_1, season_2, season_3, season_4
# 这四种不同的特征。
dummyfields = [‘season’, ‘weathersit’, ‘mnth’, ‘hr’, ‘weekday’]
for each in dummy_fields:
#利用pandas对象，我们可以很方便地将一个类型变量属性进行one-hot编码，变成多个属性_
dummies = pd.get_dummies(rides[each], prefix=each, drop_first=False)
rides = pd.concat([rides, dummies], axis=1)
# 把原有的类型变量对应的特征去掉，将一些不相关的特征去掉
fields_to_drop = [‘instant’, ‘dteday’, ‘season’, ‘weathersit’,
‘weekday’, ‘atemp’, ‘mnth’, ‘workingday’, ‘hr’]
data = rides.drop(fields_to_drop, axis=1)
data.head()
从显示出的数据中可以看到一年四季、12 个月份、24 个小时数、一周 7 天、天气情况都已经被转化成了 one-hot 变量。
2.3. 对于数值类型变量进行标准化
由于每个数值型变量都是相互独立的，所以它们的数值绝对大小与问题本身没有关系。
为了消除数值大小的差异，我们对每一个数值型变量进行标准化处理，也就是让其数值都围绕着0左右波动。
比如，对于温度 temp 这个变量来说，
它在整个数据库取值的平均值为 mean(temp)，方差为 std(temp)，所以，归一化的温度计算为：
𝑡𝑒𝑚𝑝′=𝑡𝑒𝑚𝑝−𝑚𝑒𝑎𝑛(𝑡𝑒𝑚𝑝)𝑠𝑡𝑑(𝑡𝑒𝑚𝑝)temp′=temp−mean(temp)std(temp)
这样做的好处就是可以将不同的取值范围的变量设置为让它们处于一个平等的地位。
▶ 示例代码：
In [ ]:
# 调整所有的特征，标准化处理
quantfeatures = [‘cnt’, ‘temp’, ‘hum’, ‘windspeed’]
#quantfeatures = [‘temp’, ‘hum’, ‘windspeed’]
# 我们将每一个变量的均值和方差都存储到scaled_features变量中。
scaled_features = {}
for each in quant_features:
mean, std = data[each].mean(), data[each].std()
scaled_features[each] = [mean, std]
data.loc[:, each] = (data[each] - mean)/std
2.4. 将数据集进行分割
预处理做完以后，我们的数据集包含了 17379 条记录，59 个变量。
接下来，将对这个数据集进行划分。
首先，在变量集合上，我们分为了特征和目标两个集合。
其中，特征变量集合包括：年份（yr），是否节假日（ holiday），温度（temp），湿度（hum），风速（windspeed），季节1～4（season），天气1～4（weathersit，不同天气种类），月份1～12（mnth），小时0～23（hr），星期0～6（weekday），它们是输入给神经网络的变量；
目标变量包括：用户数（cnt），临时用户数（casual），以及注册用户数（registered），其中我们仅仅将 cnt 作为我们的目标变量，另外两个暂时不做任何处理。
这样我们就将利用 56 个特征变量作为神经网络的输入，来预测 1 个变量作为神经网络的输出。
接下来，我们再将 17379 条纪录划分为两个集合，分别为前 16875 条记录作为训练集训练我们的神经网络；后 21 天的数据，也就是 21x24=504 条记录作为测试集来检验我们的模型的预测效果。这一部分数据是不参与神经网络训练的。
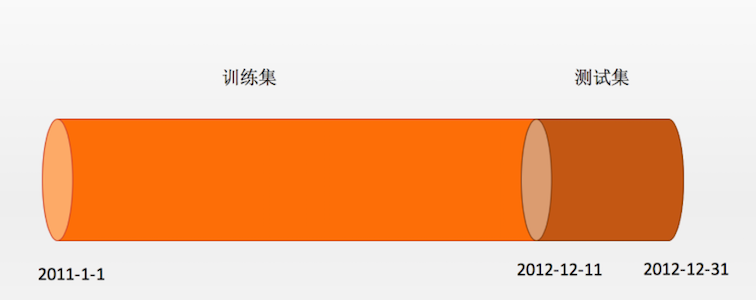
▶ 示例代码：
In [ ]:
# 将所有的数据集分为测试集和训练集，我们以后21天数据一共21*24个数据点作为测试集，其它是训练集
test_data = data[-21*24:]
train_data = data[:-21*24]
print(‘训练数据：’,len(train_data),’测试数据：’,len(test_data))
# 将我们的数据列分为特征列和目标列
#目标列
target_fields = [‘cnt’, ‘casual’, ‘registered’]
features, targets = train_data.drop(target_fields, axis=1), train_data[target_fields]
test_features, test_targets = test_data.drop(target_fields, axis=1), test_data[target_fields]
# 将数据从pandas dataframe转换为numpy
X = features.values
Y = targets[‘cnt’].values
Y = Y.astype(float)
Y = np.reshape(Y, [len(Y),1])
losses = []
features.head()
三、构建神经网络模型
3.1. 手动编写用 Tensor 运算的人工神经网络
在数据处理进行完毕后，下面将构建新的人工神经网络。
在这里，我们构建的网络有三层：输入、隐含和输出层。
每个层的尺寸（神经元个数）分别是：56、10 和 1。
其中，输入输出层的神经元个数分别由数据决定，
隐含层神经元个数则是根据我们对数据复杂度的预估决定的。
通常，数据越复杂、数据量越大，我们就需要越多的神经元。但是神经元过多很容易造成过拟合。
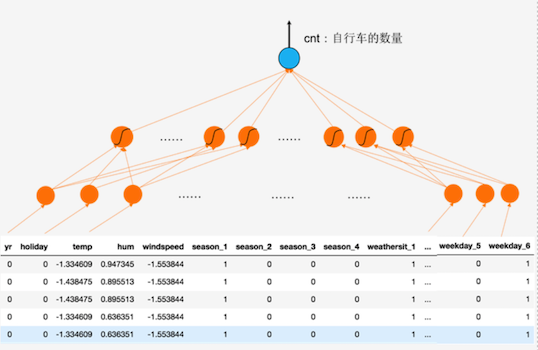
下面先用手动的麻烦的方式搭建一个神经网络，大家看不懂也不用担心，我们在下一步会使用PyTorch 提供的更方便的方式搭建一个神经网络。
▶ 示例代码：
In [ ]:
# 定义神经网络架构，features.shape[1]个输入层单元，10个隐含层，1个输出层
inputsize = features.shape[1] #输入层单元个数
hidden_size = 10 #隐含层单元个数
output_size = 1 #输出层单元个数
batch_size = 128 #每隔batch的记录数
weights1 = Variable(torch.randn([input_size, hidden_size]), requires_grad = True) #第一到二层权重
biases1 = Variable(torch.randn([hidden_size]), requires_grad = True) #隐含层偏置
weights2 = Variable(torch.randn([hidden_size, output_size]), requires_grad = True) #隐含层到输出层权重
def neu(x):
#计算隐含层输出
#x为batchsize input_size的矩阵，weights1为input_sizehidden_size矩阵，
#biases为hidden_size向量，输出为batch_size * hidden_size矩阵
hidden = x.mm(weights1) + biases1.expand(x.size()[0], hidden_size)
hidden = torch.sigmoid(hidden)
_#输入batch_size * hidden_size矩阵，mm上weights2, hidden_size*output_size矩阵，_<br /> _#输出batch_size*output_size矩阵_<br /> output **=** hidden.mm(weights2)<br /> **return** output<br />**def** cost(x, y):<br /> _# 计算损失函数_<br /> error **=** torch.mean((x **-** y)****2**)<br /> **return** error<br />**def** zero_grad():<br /> _# 清空每个参数的梯度信息_<br /> **if** weights1.grad **is** **not** **None** **and** biases1.grad **is** **not** **None** **and** weights2.grad **is** **not** **None**:<br /> weights1.grad.data.zero_()<br /> weights2.grad.data.zero_()<br /> biases1.grad.data.zero_()<br />**def** optimizer_step(learning_rate):<br /> _# 梯度下降算法_<br /> weights1.data.add_(**-** learning_rate ***** weights1.grad.data)<br /> weights2.data.add_(**-** learning_rate ***** weights2.grad.data)<br /> biases1.data.add_(**-** learning_rate ***** biases1.grad.data)
3.2. 调用PyTorch现成的函数，构建序列化的神经网络
除了前面讲过的用手工实现神经网络的张量计算完成神经网络搭建以外，
PyTorch 还实现了自动调用现成的函数来完成同样的操作，这样的代码更加简洁。
▶ 示例代码：
In [ ]:
# 定义神经网络架构，features.shape[1]个输入层单元，10个隐含层，1个输出层
input_size = features.shape[1]
hidden_size = 10
output_size = 1
batch_size = 128
neu = torch.nn.Sequential(
torch.nn.Linear(input_size, hidden_size),
torch.nn.Sigmoid(),
torch.nn.Linear(hidden_size, output_size),
)
cost = torch.nn.MSELoss()
optimizer = torch.optim.SGD(neu.parameters(), lr = 0.01)
在这段代码里，我们可以调用 torch.nn.Sequential 来构造的神经网络，并将构造好的神经网络存放到了 neu 中。
torch.nn.Sequential 这个函数的作用是将一系列的运算模块按顺序搭建成一个多层的神经网络。
在这个例子中，这些模块包括从输入到隐含层的线性映射 Linear(input_size, hidden_size)，
隐含层的非线性 Sigmoid 函数 torch.nn.Sigmoid()，以及从隐含到输出的线性映射torch.nn.Linear(hidden_size, output_size)。
值得注意的是，Sequential 里面的层次并不与神经网络的层次严格对应，而是指多步的运算，它与动态计算图的层次相对应。
我们也可以使用 PyTorch 自带的损失函数：
cost = torch.nn.MSELoss()
这里 torch.nn.MSELoss 是 PyTorch 自带的一个封装好的计算均方误差的损失函数，它是一个函数指针，赋予了变量 cost。在计算的时候我们只需要调用 cost(x,y) 就可以计算预测向量 x 和目标向量 y 之间的均方误差。
除此之外，PyTorch 也自带了优化器来自动实现优化算法：
optimizer = torch.optim.SGD(neu.parameters(), lr = 0.01)
这里 torch.optim.SGD 调用了 PyTorch 自带的随机梯度下降算法（Stochastic Gradient Descent，SGD）作为优化器。
在初始化 optimizer 的时候，我们需要将待优化的所有参数（在本例中就是传入的参数包括神经网络neu包含的所有权重和偏置（即neu.parameters()），以及执行梯度下降算法的学习率lr=0.01。在一切的材料都准备好之后，就可以实施训练了。
3.3 数据的分批次处理
然而，在进行训练循环的时候，我们还会遇到一个问题。
如果在每一个训练周期都是将所有的数据一股脑儿地喂给神经网络。
这在数据量不大的情况下没有任何问题。
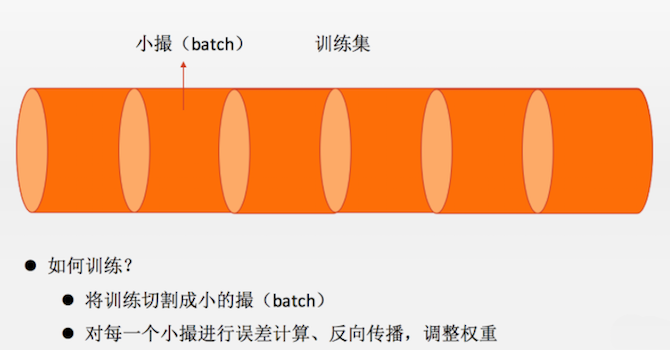
但是，我们现在的数据量是 16875 条，在这么大数据量的情况下如果还是在每个训练周期处理所有数据，那么可能会出现，运算速度过慢，迭代可能不收敛的问题。
人们通常采用的解决方法是批处理（batch processing）的模式，也就是将所有的数据记录划分成一个批次大小（batch size）的小数据集，然后每个训练周期喂给神经网络一批数据。
如下图所示。通常，批的大小依问题的复杂度和数据量的大小而定，在我们这个试验中，我们设定 batch_size = 128。
▶ 示例代码：
In [ ]:
# 神经网络训练循环
losses = []
for i in range(1000):
# 每128个样本点被划分为一个撮，在循环的时候一批一批地读取
batchloss = []
# start和end分别是提取一个batch数据的起始和终止下标_
for start in range(0, len(X), batch_size):
end = start + batch_size if start + batch_size < len(X) else len(X)
xx = Variable(torch.FloatTensor(X[start:end]))
yy = Variable(torch.FloatTensor(Y[start:end]))
predict = neu(xx)
loss = cost(predict, yy)
optimizer.zero_grad()
loss.backward()
optimizer.step()
batch_loss.append(loss.data.numpy())
_# 每隔100步输出一下损失值（loss）_<br /> **if** i **%** **100==0**:<br /> losses.append(np.mean(batch_loss))<br /> print(i, np.mean(batch_loss))
由于在线环境资源有限，此步骤的代码执行需要较长的时间，需要大家耐心等待。（大概预计在30分钟左右）需要提醒的就是，在线环境有效时间是1个小时，若时间不够，请记得点击工具栏的延时。
下面打印输出损失值。
▶ 示例代码：
In [ ]:
# 打印输出损失值
fig = plt.figure(figsize=(10, 7))
plt.plot(np.arange(len(losses))*100,losses, ‘o-‘)
plt.xlabel(‘epoch’)
plt.ylabel(‘MSE’)
在上段代码绘制出的图中，横坐标表示训练周期，纵坐标表示平均误差。
可以看到，平均误差快速地随训练周期而下降
四、测试网络
4.1 使用测试数据集测试网络
接下来，我们便可以用训练好的神经网络在测试集上进行预测，并且将后21天的预测数据与真实数据画在一起做比较。
▶ 示例代码：
In [ ]:
# 用训练好的神经网络在测试集上进行预测
targets = testtargets[‘cnt’] #读取测试集的cnt数值
targets = targets.values.reshape([len(targets),1]) #将数据转换成合适的tensor形式
targets = targets.astype(float) #保证数据为实数_
# 将属性和预测变量包裹在Variable型变量中
x = Variable(torch.FloatTensor(test_features.values))
y = Variable(torch.FloatTensor(targets))
# 用神经网络进行预测
predict = neu(x)
predict = predict.data.numpy()
# 将后21天的预测数据与真实数据画在一起并比较
# 横坐标轴是不同的日期，纵坐标轴是预测或者真实数据的值
fig, ax = plt.subplots(figsize = (10, 7))
mean, std = scaledfeatures[‘cnt’]
ax.plot(predict * std + mean, label=‘Prediction’, linestyle = ‘—‘)
ax.plot(targets * std + mean, label=‘Data’, linestyle = ‘-‘)
ax.legend()
ax.set_xlabel(‘Date-time’)
ax.set_ylabel(‘Counts’)
# 对横坐标轴进行标注
dates = pd.to_datetime(rides.loc[test_data.index][‘dteday’])
dates = dates.apply(lambda d: d.strftime(‘%b %d’))
ax.set_xticks(np.arange(len(dates))[12::24])
= ax.set_xticklabels(dates[12::24], rotation=45)
4.2 预测结果分析
在上一步的代码绘制的图中，横坐标是不同的日期，纵坐标是预测或真实数据的值。
通过数据的可视化，我们可以观察到两个曲线基本是吻合的，但是在 12 月 25 日附近几天实际值和预测值偏差较大。为什么这段时间表现这么差呢？
仔细观察数据，我们知道 12 月 25 日正好是圣诞节。对于欧美国家来说，圣诞节就相当于是我们的春节，而从圣诞节之后的一周直到元旦都是假期。因此，在圣诞节的前后人们的出行习惯肯定会与往日有很大的不同。但是，在我们的训练样本中，因为整个数据仅仅有两年的长度，所以包含圣诞节前后的样本仅仅有一次，这就导致我们没办法对这一特殊假期的模式进行很好地预测。
五、实验总结
至此，本实验结束，我们对本实验所经历的过程进行总结：
- 1.我们学习了使用神经网络模型解决实际问题的方法。
- 2.我们了解到对数据预处理的一些方法。
- 3.我们熟悉了搭建神经网络的一般流程。
- 4.我们了解到测试神经网络、简单分析神经网络的方法。
通过本次实验，我们才第一次接触到深度神经网络模型的真正应用，我们发现它真的可以在实际问题中取得很好的效果。
当然，现实中深度学习要解决的问题往往不像例子中那么简单，但是我们本系列的实验也刚刚开始，只要你有兴趣有毅力探索下去，还有什么问题是人类解决不了的哪？
若有收获，就点个赞吧
0 人点赞
