在概率图模型中，数据(样本)由公式
建模表示：
表示节点，即随机变量(放在此处的，可以是一个token或者一个label)，具体地，用
为随机变量建模，注意
现在是代表了一批随机变量(想象对应一条sequence，包含了很多的token)，
为这些随机变量的分布；
表示边，即概率依赖关系。
有向图vs.无向图
上图可以看到，贝叶斯网络（信念网络）都是有向的，马尔科夫网络无向。所以，贝叶斯网络适合为有单向依赖的数据建模，马尔科夫网络适合实体之间互相依赖的建模。具体地，他们的核心差异表现在如何求
，即怎么表示
这个的联合概率。
有向图
对于有向图模型，这么求联合概率：
举个例子，对于下面的这个有向图的随机变量(注意，这个是比较广义的)：
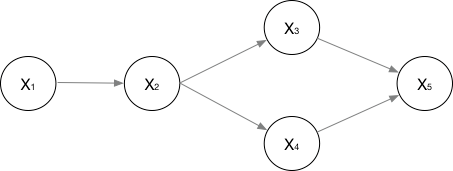
应该这样表示他们的联合概率:
无向图
对于无向图，我看资料一般就指马尔科夫网络(注意，这个图我也是比较广义的)。
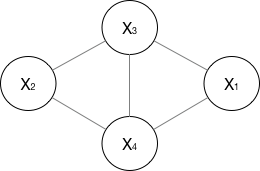
如果一个graph太大，可以用因子分解将
写为若干个联合概率的乘积。咋分解呢，将一个图分为若干个“小团”，注意每个团必须是“最大团”（就是里面任何两个点连在了一块，具体……算了不解释，有点“最大连通子图”的感觉），则有：
，其中 
归一化是为了让结果算作概率，所以像上面的无向图：
其中，
是一个最大团
上随机变量们的联合概率，一般取指数函数的：
好了，这个叫做势函数。注意
是否有看到CRF的影子。
那么概率无向图的联合概率分布可以在因子分解下表示为：
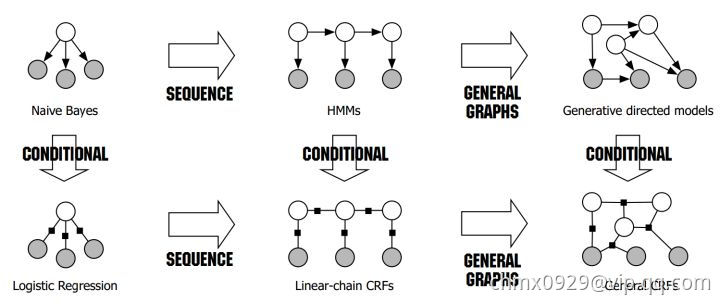
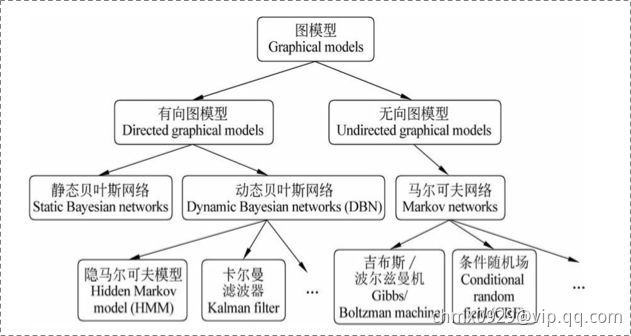
概率图联系
Source
若有收获，就点个赞吧
0 人点赞
