社区检测与社区搜索比较
| Community Detection | Community Search | |
|---|---|---|
| Goal | Find all communities with a global criterion | Find communities for particular persons |
| Cost | Expensive | Less expensive |
| Status | Graphs evolve | Online and dynamic |
常规算法比较
度量指标:1、计算时间复杂度;2、精确度(与实际标签比较、计算标准化互信息);3、有效性(聚类系数、模块度、强度);4、密度敏感性;5、混合社区敏感点;6、离群点检测。
基于下图可以看到,LPA(标签传播算法)和HANP(基于LPA的改进)效果好且高效。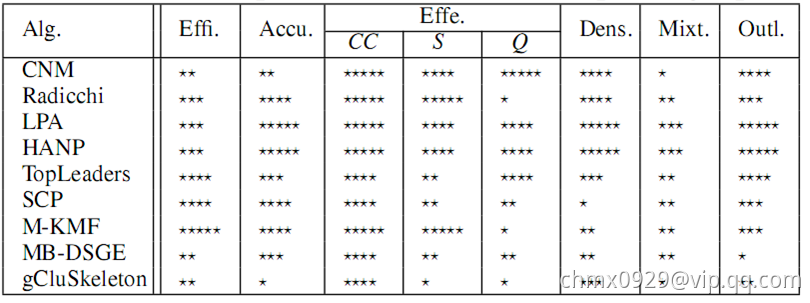
聚类
层次化聚类
输入:给以网络(邻接矩阵)
- 由网络结构计算距离矩阵
- 距离确定节点相似度(相邻即
,隔最少
个相连即
)
- 根据相似度从强到弱递归合并节点
- 根据实际需求横切树状图(如下图要分
类,可在
切一刀:分为绿色,样本6,样本3,4)
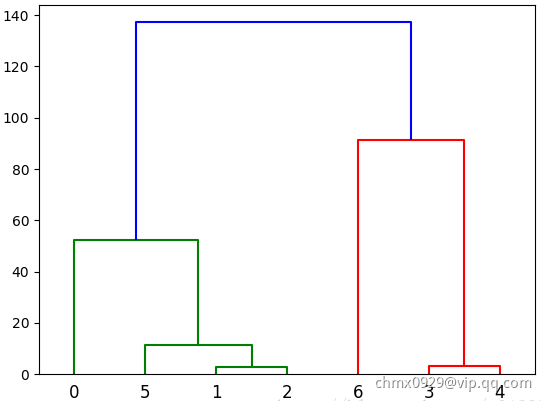
谱聚类
将图切分成相互没有连接的
个子图:
,要求
且
,设
为边权重,优化目标为
将划分问题转化为求解拉普拉斯矩阵的个最小特征值问题。
算法过程:
- 构建拉普拉斯矩阵:
,其中
:度矩阵(对角矩阵),
:邻接矩阵
- 标准化:
- 求最小的
个特征值对应的特征向量(降维)
- 标准化后再用常规方法(k-means等)聚为
各类
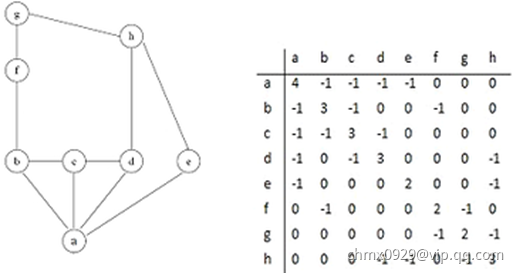
图划分
目标:划分为近似相等的分区,同时边切边最小。(明尼苏达大学的METIS是最权威的图划分工具)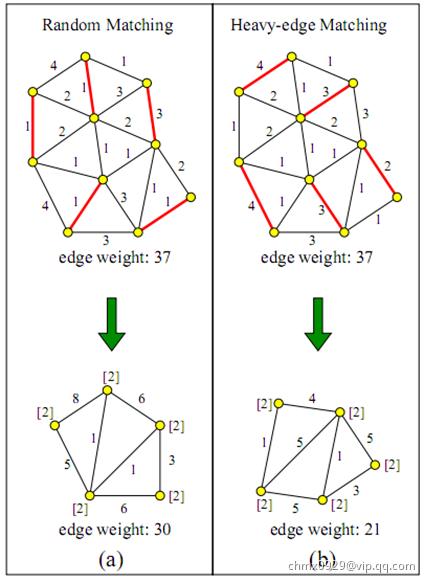
分裂算法-GN算法
思想:
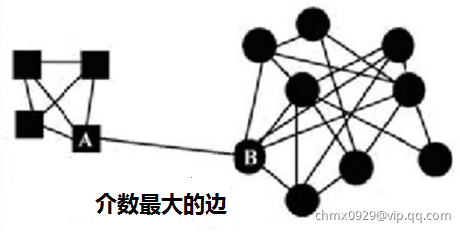
- 定义边介数(betweenness)指标:衡量的是网络里一个边占据其它节点间捷径的程度
- 具有高边介数的边代表了社区的边界
边介数最常见的定义:图中通过该边的所有最短路径数量。如下图和
之间的边即当前最可能切除的
算法过程:
- 找到网络中具有最大边介数的边
- 删除该边
- 重复1.和2.,直到所有边被移除或数量已满足要求
类
模块度优化算法
思想:
- 定义模块度(Modularity)指标:衡量一个社区的划分好坏
- 以模块度为目标进行优化;例如在层次化聚类中使用贪婪算法
一种模块度的定义:
假设网络被划分为个社区,那么定义一个
的对称矩阵
,它的元素
表示社区
和社区
之间的边的数量占比。
表示连接社区
的边的总数占比。
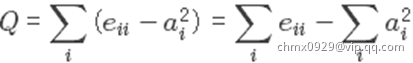
举例如下:
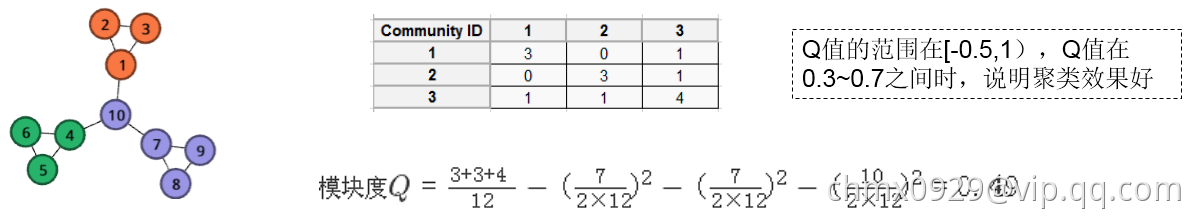
有小伙伴会疑惑,上图例子里这个7咋来的,这个10又咋来的?其实图链接被看作是双向的,所以完整的计算公式应该如下,第二部分分子3是社区1内有3个边,双向的所以乘以2,再加节点1有一个连接到社区外节点10的边,所以是2乘以3再加1:
标签传播算法
启发式规则:一个节点应该与多数邻居在同一社区内。特点:适合半监督和无监督、效率很高适合大规模、存在震荡->采取异步更新、结果可能不稳定
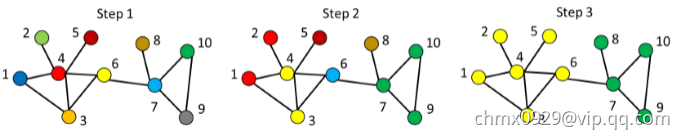
算法过程:
- 给每个节点初始化一个标签
- 在网络中传播标签
- 选择邻居的标签中数量最多的进行更新(若有相同数量标签时,选择具有最高ID的标签)
- 重复步骤2和3,直到收敛或满足迭代次数
随机游走
思想:
- 从节点出发随机游走,停留在社区内的概率高于到达社区外的。
- 重复随机游走,强化并逐渐显现社区结构。
算法过程:
- 建立邻接矩阵(含自环)
- 标准化转移概率矩阵
- Expansion操作,对矩阵计算
次幂方
- Inflation操作,对矩阵元素计算
次幂方并标准化(这一步将强化紧密的点,弱化松散的点)
- 重复直到稳定
- 对结果矩阵进行常规聚类
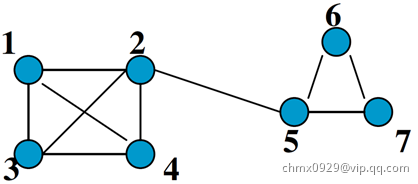

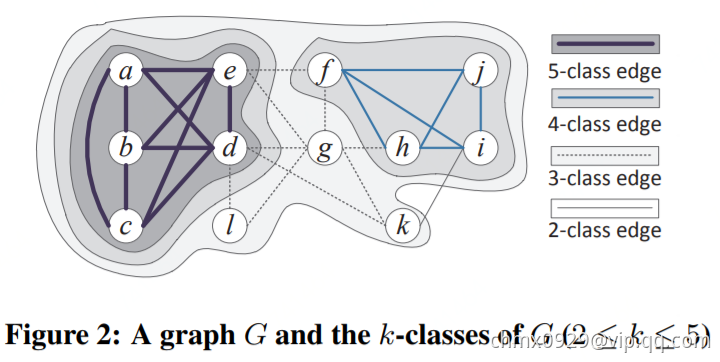
K-Truss
给以图,K-truss定义为:每个在最大的子图
中的边至少在
个存在于
的三角形中,如下左图
- K-truss: each edge within at least
triangles
- Edge Connectivity: common edges shared by triangles
- Maximal Subgraph
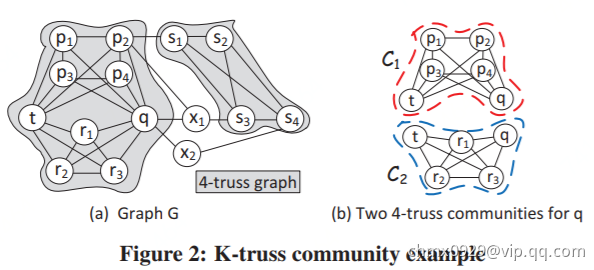
其它算法
派系过滤算法(clique percolation algorithm)- 社区的网络
领导力扩张(Leadership expansion)- 类似与kmeans
基于聚类系数的方法(Maximal K-Mutual friends)- 目标函数优化
HANP(Hop attenuation & node preference)- LPA增加节点传播能力
SLPA(Speak-Listen Propagation Algorithm)- 记录历史标签序列
Matrix blocking – 根据邻接矩阵列向量的相似性排序
Skeleton clustering – 映射网络到核心连接树后进行检测
算法在实现时通常需要关注:同步/异步,节点遍历方式,平局决胜,迭代终止,超大社区,串行/并行等问题。
Source
https://arxiv.org/pdf/1205.6693.pdf
https://arxiv.org/pdf/cs/0504107.pdf
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.722.9193&rep=rep1&type=pdf
http://keg.cs.tsinghua.edu.cn/jietang/publications/TKDE13-Sun-etl-al-co-evolution-of-multi-typed-objects-in-dynamic-networks.pdf

