高维及庞大项集
初始化:利用一个算法挖掘粗所有项比较少的频繁项集,比如3-项集迭代:在每一轮,随机从当前的模式池选择出K种子模式对于每个的选择出的种子模式,我们找到所有以种子模式为中心且在界限内的模式(聚类)所有这些被找到的模式融合一起生成一个父模式集合所有的父模式集合作为下一轮的模式池进入下一次迭代终止:在此轮迭代开始时,当前模式池包含不超过K模式
序列模式
项集数据和序列数据
首先我们看看项集数据和序列数据有什么不同,如下图所示。
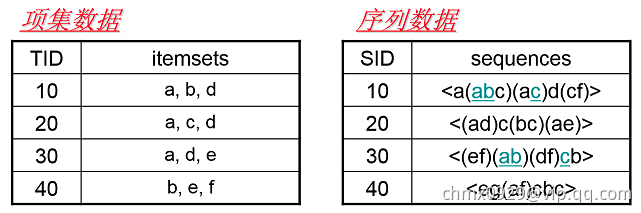
左边的数据集就是项集数据,在Apriori和FP Tree算法中我们也已经看到过了,每个项集数据由若干项组成,这些项没有时间上的先后关系。而右边的序列数据则不一样,它是由若干数据项集组成的序列。比如第一个序列,它由a,abc,ac,d,cf共5个项集数据组成,并且这些项集有时间上的先后关系。对于多于一个项的项集我们要加上括号,以便和其他的项集分开。同时由于项集内部是不区分先后顺序的,为了方便数据处理,我们一般将序列数据内所有的项集内部按字母顺序排序。
注:序列模式的序列是指项集是有相互顺序的,但项集内部是没有顺序的。
子序列与频繁序列
了解了序列数据的概念,我们再来看看什么是子序列。子序列和我们数学上的子集的概念很类似,也就是说,如果某个序列所有的项集在序列
中的项集都可以找到,则
就是
的子序列。当然,如果用严格的数学描述,子序列是这样的:
对于序列和序列
,如果存在数字序列
,满足
,则称
是
的子序列。当然反过来说,
是
的超序列。
而频繁序列则和我们的频繁项集很类似,也就是频繁出现的子序列。比如对于下图,支持度阈值定义为50%,也就是需要出现两次的子序列才是频繁序列。而子序列是频繁序列,因为它是图中的第一条数据和第三条序列数据的子序列,对应的位置用蓝色标示。

GSP

SPADE
PrefixSpan
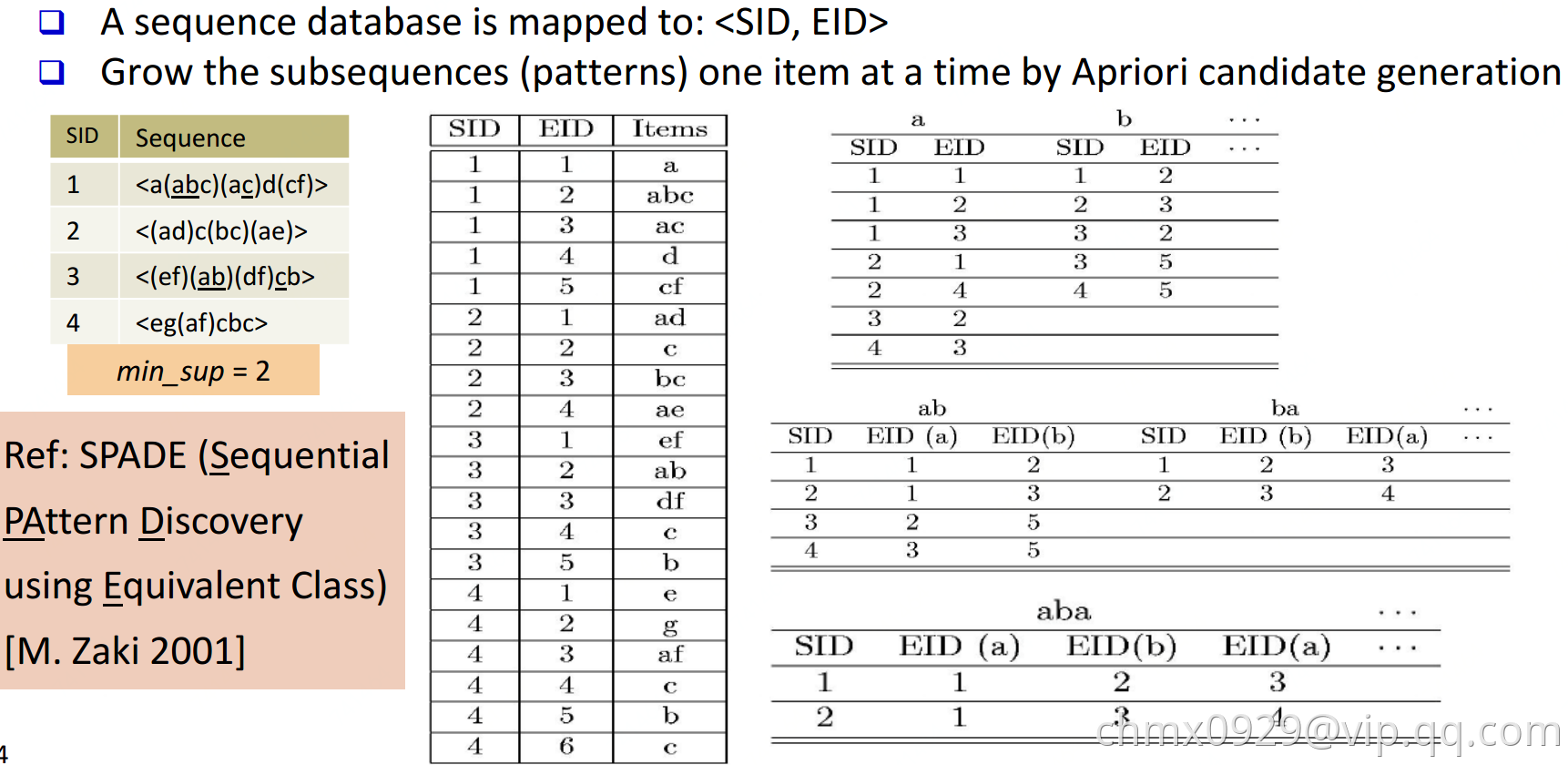
PrefixSpan算法的全称是Prefix-Projected Pattern Growth,即前缀投影的模式挖掘。里面有前缀和投影两个词。那么我们首先看看什么是PrefixSpan算法中的前缀prefix。
在PrefixSpan算法中的前缀prefix通俗意义讲就是序列数据前面部分的子序列。如果用严格的数学描述,前缀是这样的:序列和序列
,
。满足
,而
,则称
是
的前缀。比如对于序列数据
,而
,则
是
的前缀。当然
的前缀不止一个,比如
也是
的前缀。
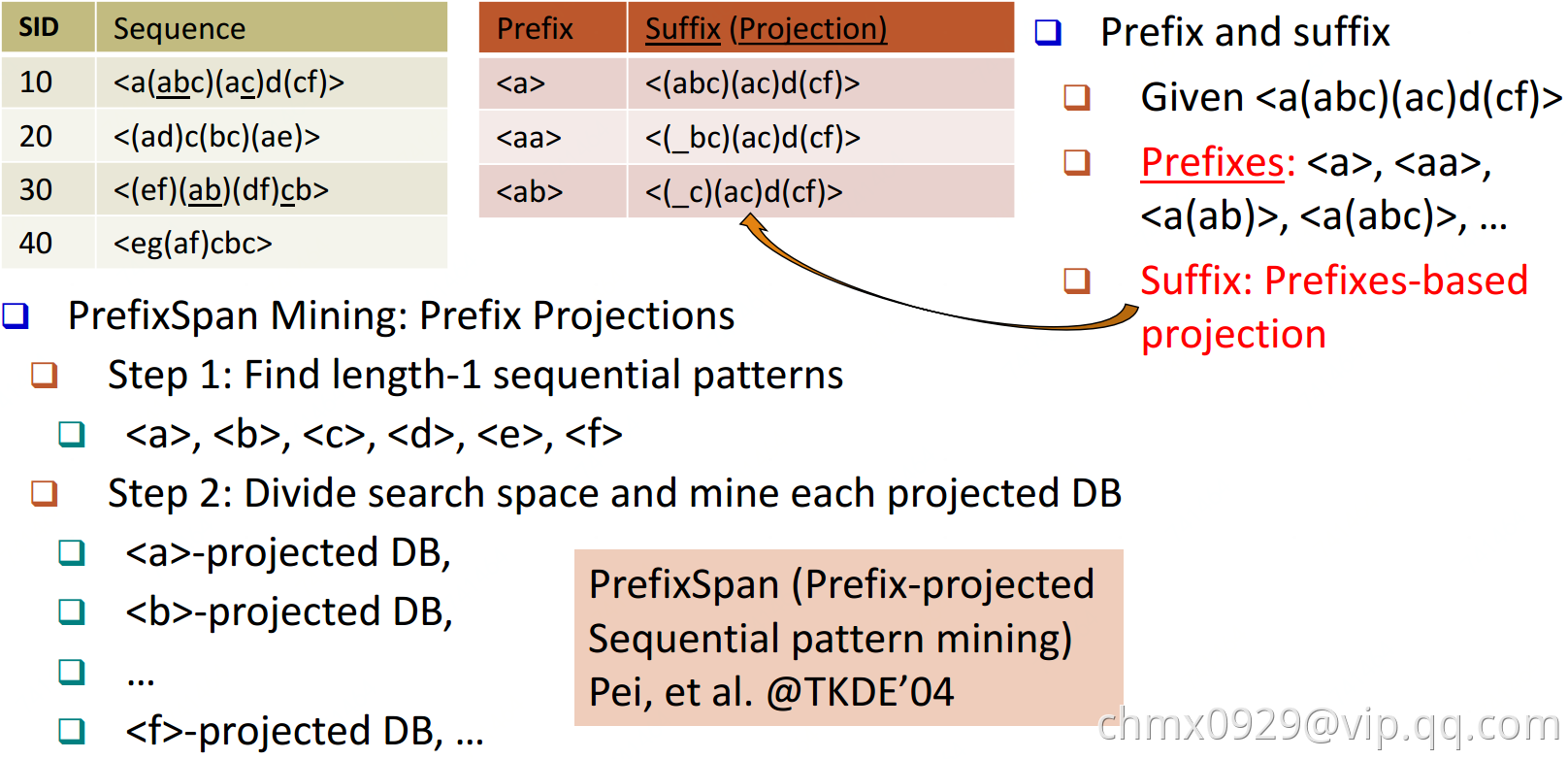
看了前缀,我们再来看前缀投影,其实前缀投影这儿就是我们的后缀,有前缀就有后缀嘛。前缀加上后缀就可以构成一个我们的序列。下面给出前缀和后缀的例子。对于某一个前缀,序列里前缀后面剩下的子序列即为我们的后缀。如果前缀最后的项是项集的一部分,则用一个“_”来占位表示。
下面这个例子展示了序列的一些前缀和后缀,还是比较直观的。要注意的是,如果前缀的末尾不是一个完全的项集,则需要加一个占位符。
在PrefixSpan算法中,相同前缀对应的所有后缀的结合我们称为前缀对应的投影数据库。

PrefixSpan算法由于不用产生候选序列,且投影数据库缩小的很快,内存消耗比较稳定,作频繁序列模式挖掘的时候效果很高。比起其他的序列挖掘算法比如GSP,FreeSpan有较大优势,因此是在生产环境常用的算法。
PrefixSpan运行时最大的消耗在递归的构造投影数据库。如果序列数据集较大,项数种类较多时,算法运行速度会有明显下降。因此有一些PrefixSpan的改进版算法都是在优化构造投影数据库这一块。比如使用伪投影计数。
不过scikit-learn始终不太重视关联算法,一直都不包括这一块的算法集成。当然使用大数据平台的分布式计算能力也是加快PrefixSpan运行速度一个好办法。比如Spark的MLlib就内置了PrefixSpan算法。
算法思路
现在我们来看看PrefixSpan算法的思想,PrefixSpan算法的目标是挖掘出满足最小支持度的频繁序列。那么怎么去挖掘出所有满足要求的频繁序列呢。回忆Aprior算法,它是从频繁1项集出发,一步步的挖掘2项集,直到最大的K项集。PrefixSpan算法也类似,它从长度为1的前缀开始挖掘序列模式,搜索对应的投影数据库得到长度为1的前缀对应的频繁序列,然后递归的挖掘长度为2的前缀所对应的频繁序列…以此类推,一直递归到不能挖掘到更长的前缀挖掘为止。
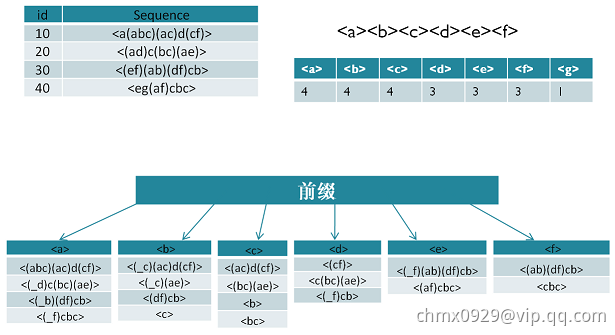
比如对应于我们第二节的例子,支持度阈值为50%。里面长度为1的前缀包括,我们需要对这7个前缀分别递归搜索找各个前缀对应的频繁序列。如下图所示,每个前缀对应的后缀也标出来了。由于
只在序列4出现,支持度计数只有1,因此无法继续挖掘。我们的长度为1的频繁序列为
。去除所有序列中的
,即第4条记录变成
。
现在我们开始挖掘频繁序列,分别从长度为1的前缀开始。这里我们以为例子来递归挖掘,其他的节点递归挖掘方法和
一样。
方法如下图,首先我们对的后缀进行计数,得
。注意
和
不一样的,因为前者是在和前缀
不同的项集,而后者是和前缀
同项集。由于此时
都达不到支持度阈值,因此我们递归得到的前缀为
的2项频繁序列为
和
。
接着我们分别递归和
为前缀所对应的投影序列。首先看
前缀,此时对应的投影后缀只有
,此时
支持度均达不到阈值,因此无法找到以
为前缀的频繁序列。现在我们来递归另外一个前缀
。以
为前缀的投影序列为
,此时进行支持度计数,结果为
,只有
满足支持度阈值,因此我们得到前缀为
的三项频繁序列为
。
我们继续递归以为前缀的频繁序列。由于前缀
对应的投影序列
支持度全部不达标,因此不能产生4项频繁序列。至此以
为前缀的频繁序列挖掘结束,产生的频繁序列为
。
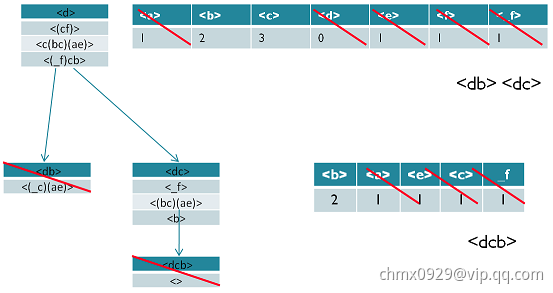
同样的方法可以得到其他以为前缀的频繁序列。
算法流程
输入:序列数据集和支持度阈值
输出:所有满足支持度要求的频繁序列集
- 找出所有长度为1的前缀和对应的投影数据库
- 对长度为1的前缀计数,将支持度低于阈值
的前缀项从数据集
删除,同时得到所有的频繁1项序列,
- 对于每个长度为
满足支持度要求的前缀进行递归挖掘:
- 找出前缀所对应的投影数据库。如果投影数据库为空,则递归返回
- 统计对应投影数据库中各项的支持度计数。如果所有项的支持度计数都低于阈值
,则递归返回
- 将满足支持度计数的各个单项和当前的前缀进行合并,得到若干新的前缀
- 令
,前缀为合并单项后的各个前缀,分别递归执行第3步
Code实现
https://spark.apache.org/docs/2.3.0/mllib-frequent-pattern-mining.html
from pyspark import SparkContextfrom pyspark import SparkConffrom pyspark.mllib.fpm import PrefixSpansc = SparkContext("local","testing")data = [[['a'],["a", "b", "c"], ["a","c"],["d"],["c", "f"]],[["a","d"], ["c"],["b", "c"], ["a", "e"]],[["e", "f"], ["a", "b"], ["d","f"],["c"],["b"]],[["e"], ["g"],["a", "f"],["c"],["b"],["c"]]]rdd = sc.parallelize(data, 2)model = PrefixSpan.train(rdd, 0.5,4)sorted(model.freqSequences().collect())
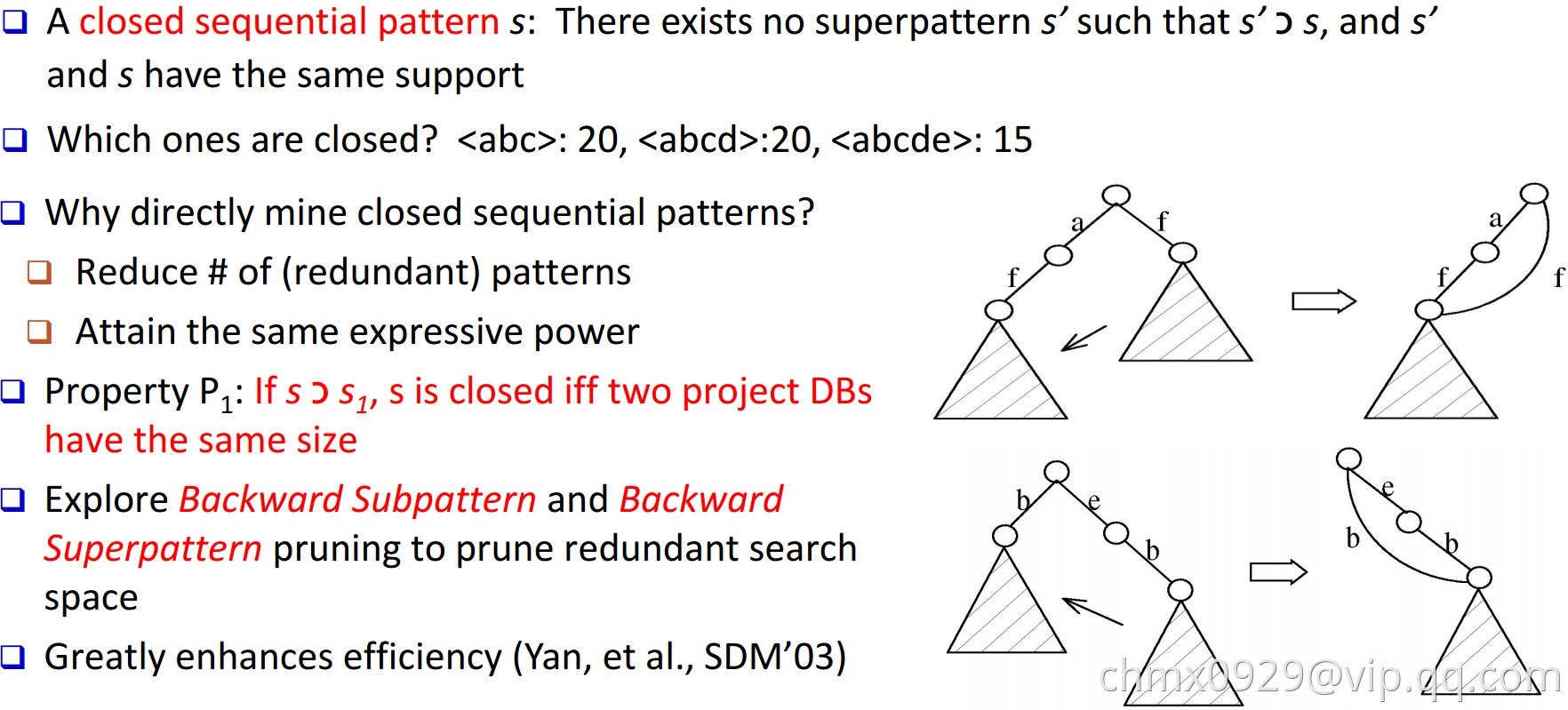
CloSpan(针对closed sequential patterns)
基于约束的序列模式挖掘

基于时间约束的序列模式挖掘

图模式
方法分类
候选集生成方式:Apriori vs. Pattern growth (FSG vs. gSpan)
搜索顺序:广度 vs. 深度
重复子图剔除:被动 vs. 主动(gSpan)
支持度计算:GASTON, FFSM, MoFa
模式发现顺序:Path->Tree->Graph (GASTON)
基于Apriori的方法
候选集生成 -> 候选集剪枝 -> 支持度计算 -> 候选集剔除 迭代这四步至无法生成候选集或不满足支持度
候选集生成时扩展节点(AGM算法)还是扩展边(FSG算法)都可以,但是经测试是扩展边更高效
基于Pattern-Growth的方法
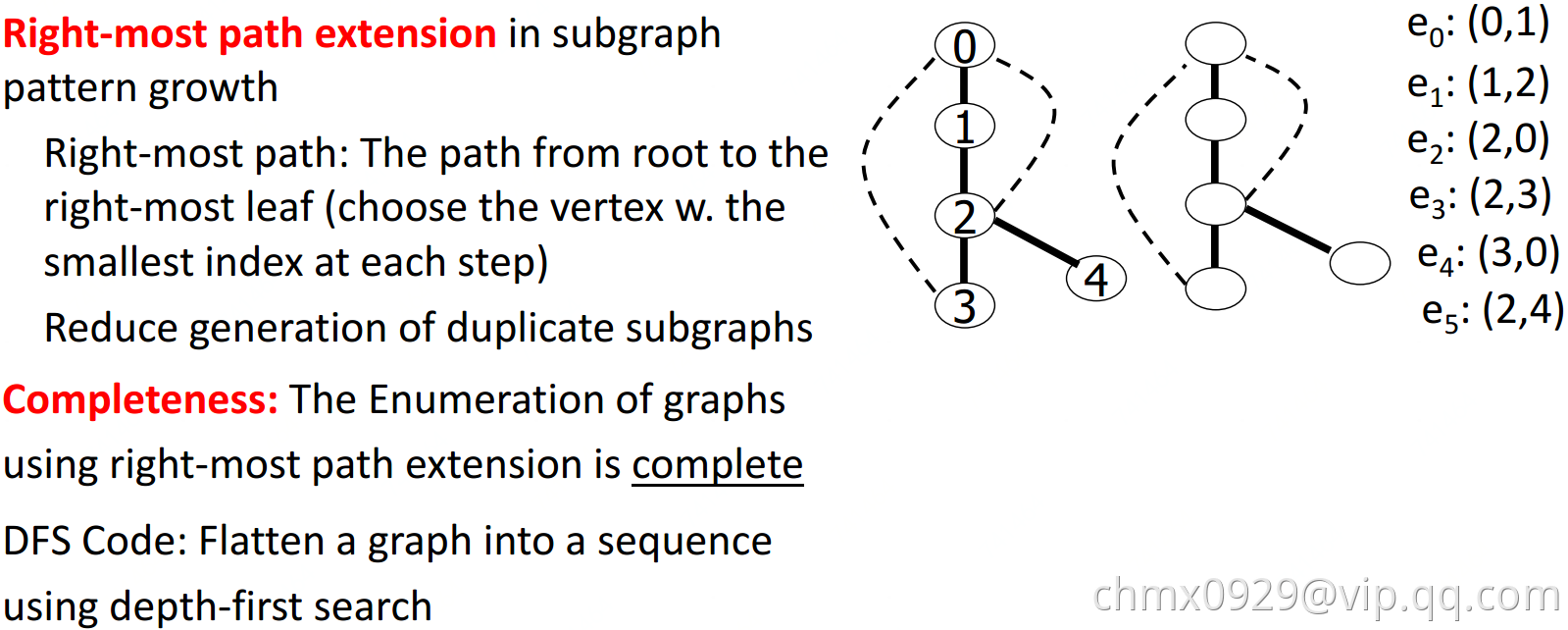
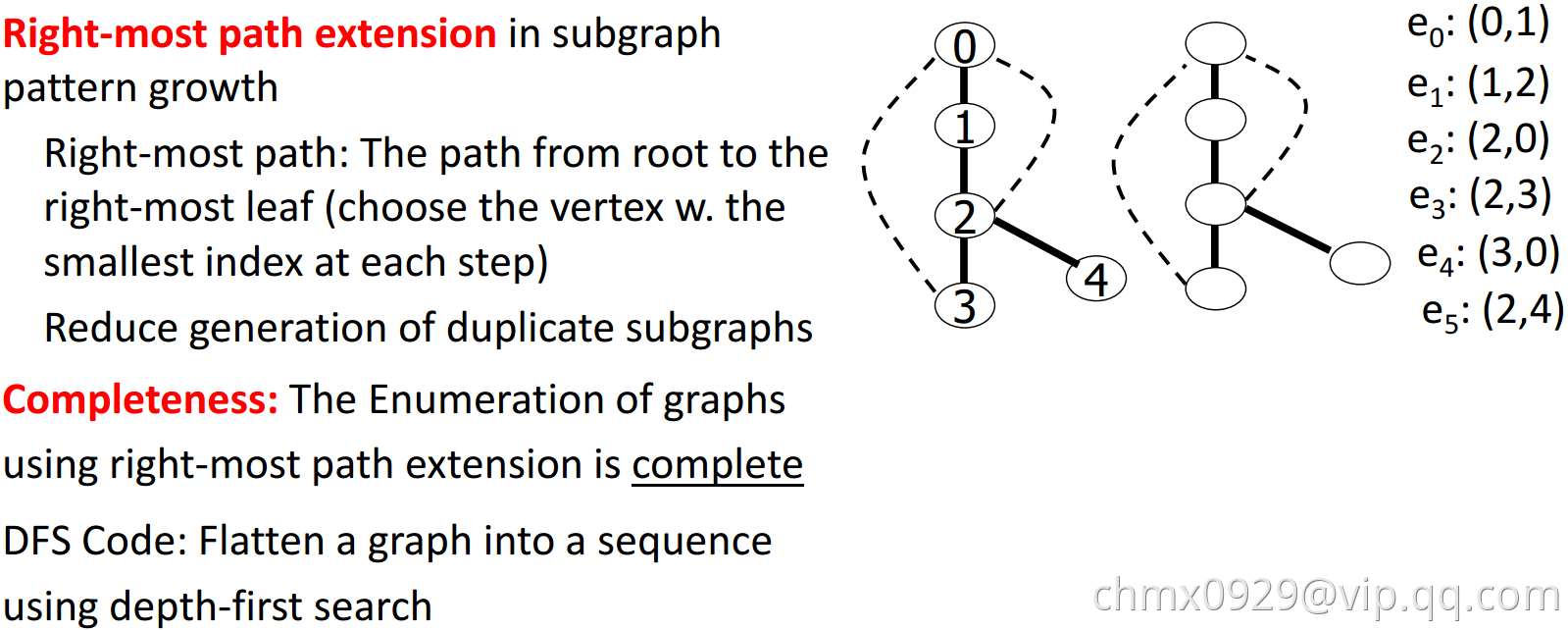
按深度优先来扩展边,从k边子图->(k+1)边子图->(k+2)边子图…
问题:这样会生成很多重复子图
解决:1、定义一个子图生成顺序 2、DFS生成树,用深度优先搜索扁平图 3、gSpan
gSpan