无约束优化

梯度下降法(Gradient descent)

梯度下降法(Gradient descent)或最速下降法(Steepest descent)是求解无约束最优化问题的一种最常见的方法，有实现简单的有点。梯度下降法是迭代算法，每一步需要求解目标函数的梯度向量。

假设是是具有一阶连续偏导数的函数，要求解的无约束最优化问题是：

梯度下降法是一种迭代算法，选取适当的初值，不断迭代，更新的值，进行目标函数的极小化，直到收敛。由于负梯度方向是使函数值下降最快的方向，在迭代的每一步，以负梯度方向更新的值，从而达到减少函数值的目的。

由于具有一阶连续偏导数，若第次迭代值为，则可将在附近进行一阶泰勒展开

这里，为在的梯度，求出第次迭代值

其中，是搜索方向，取负梯度方向，是步长，由一维搜索确定，即使得

具体算法

输入：目标函数，梯度函数，计算精度；输出：的极小点

1. 取初始值，置
2. 计算
3. 计算梯度：
   1. 当时，停止迭代，令
   2. 否则，令，求，使
4. 置，计算
   1. 当或时，停止迭代，令
5. 否则，置，转3.

当目标函数是凸函数时，梯度下降法的解是全局最优解。一般情况下，其解不保证是全局最优解，梯度下降法的收敛速度也未必是很快的。

牛顿法(Newton’s method)

优化问题的最优解一般出现在极值点上，也就的解，所以，牛顿法求解优化问题即求的零点。

首先，随机选择初始值，对于函数，计算相应的和切线斜率(这里即表示的导数)。然后我们计算穿过点并且斜率为的直线和轴的交点的坐标，也就是

我们将新求得点的坐标命名为，通常会比更接近方程的解，处其实并不是完全相等的，而是近似相等，因为只做了一阶泰勒展开，当进行了无限阶泰勒展开全加起来才是等式。由于相对而言一阶变换量是最大的，所以我们先只考虑一阶展开）。因此我们可以利用开始下一轮迭代。迭代公式可简化为下式：

通过迭代，这个式子必在的时候收敛，具体过程如下图。

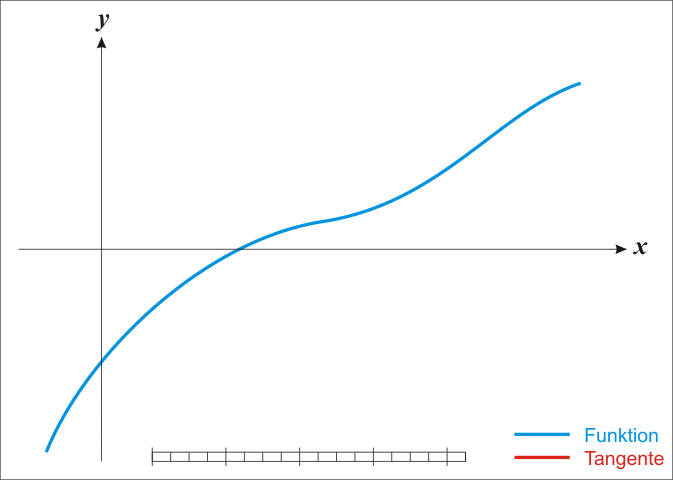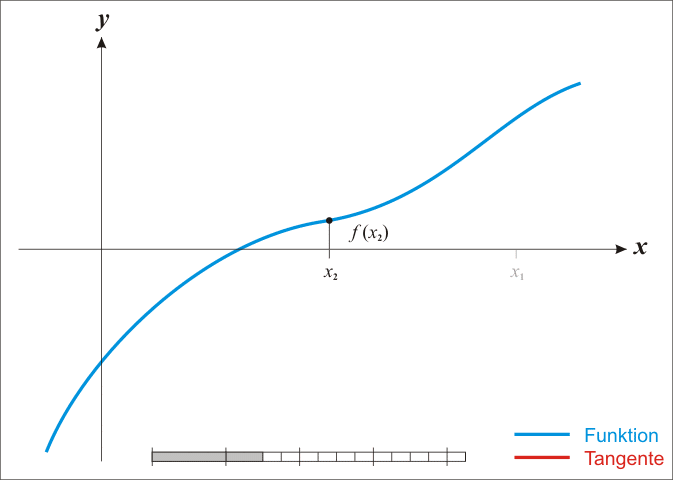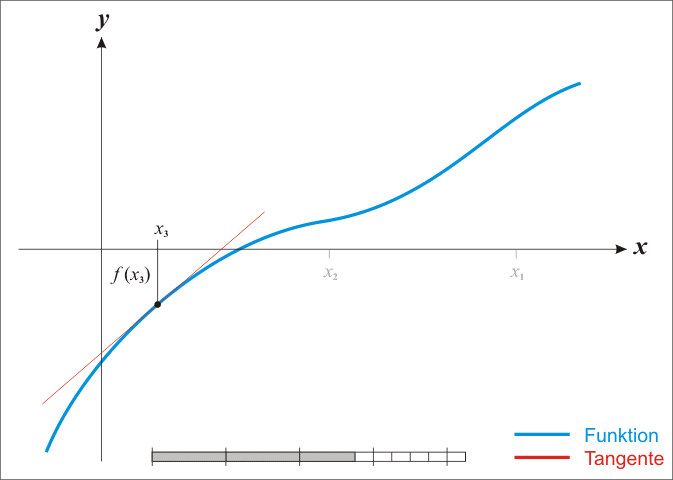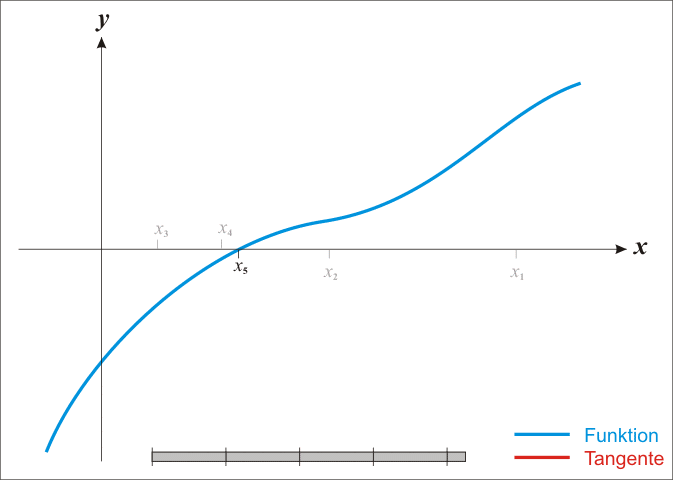
在优化问题中，其任务就是优化一个目标函数，求这个函数的极大极小问题，可以转化为求解函数的导数的问题了。这就和上面说的牛顿求解很相似了。

为了求导数的根，我们要把在探索点处泰勒展开，展开到二阶泰勒近似，即要考虑导数的导数：

我们考虑二阶导，即导数的导数：

求得迭代公式：

上面解释了牛顿法的优化，都是以一维举例的（就一个变量）。从一维问题的迭代推广至多维问题只需将导数替换为梯度，并将二阶导数的倒数替换为Hessian矩阵的逆矩阵，即：

通常，使用牛顿法时会加入一个步长变量作微调，即：

这个方法即被称为无约束牛顿法，通常用于第一步之后的迭代。

统计学习方法（李航）牛顿法详解

考虑无约束最优化问题：

假设具有二阶连续偏导数，若第次迭代值为，则可将在附近进行二阶泰勒展开

这里，是的梯度向量在点的值，是的Hessian矩阵

函数有极值的必要条件是在极值点处一阶导数为0，即梯度向量为0特别是当是正定矩阵时，函数的极值为极小值。牛顿法利用极小值的必要条件，每次迭代从点开始，求目标函数的极小点，作为第次迭代值，具体地，假设满足结合泰勒展开则有

其中，这样

因此，

将上式作为迭代公式的算法就是牛顿法。

具体算法

输入：目标函数，梯度，海塞矩阵，精度要求

输出：的极小点

1. 取初始值，置
2. 计算
3. 若，则停止计算，得近似解
4. 计算，并求：
5. 置
6. 置，转2.

应用举例

我们刷leetcode时有这样一道题，求解平方根(只保留整数部分)。牛顿迭代法是已知的实现求方根最快的方法之一，只需要迭代几次后就能得到相当精确的结果。设的次方根为，则推导公式如下：

代入牛顿法公式

代码如下(求平方根，即，)：

class Solution:
    def mySqrt(self, a):
        x = a
        while x > a / x:
            x = (x + a / x) // 2
        return int(r)

拟牛顿法(quasi-Newton method)

在牛顿法的迭代中，需要计算海赛矩阵的逆矩阵，这一计算比较复杂，考虑用一个阶矩阵来近似替代。这就是拟牛顿法的基本想法。先看牛顿法迭代中海赛矩阵满足的条件。首先，满足以下关系。在中取，得

记，，则

或

上式即称为拟牛顿条件。如果是正定的(也是正定的)，那么可以保证牛顿法搜索方向是下降方向。这是因为搜索方向是，结合牛顿法迭代式有

所以在的泰勒展开式可以近似写成

因正定，故有当为一个充分小的正数时，总有，也就是说是下降方向。

拟牛顿法将作为的近似，要求矩阵满足同样的条件。首先，每次迭代矩阵是正定的。同时，满足下面的拟牛顿条件：

按照拟牛顿条件选择作为的近似或选择作为的近似的算法称为拟牛顿法。按照拟牛顿条件，在每次迭代中可以选择更新矩阵：

DFP

DFP算法选择的方法是，假设每一步迭代中矩阵是由加上两个附加项构成的，即

其中，是待定矩阵。这时，

为使满足拟牛顿条件，可使和满足：

事实上，不难找出这样的和，例如取

这样就可得到矩阵的迭代公式：

称为DFP算法。可以证明，如果初始矩阵是正定的，则迭代过程中的每个矩阵都是正定的。

输入：目标函数，梯度，精度要求；输出：的极小点

1. 选定初始点，取为正定对称矩阵，置
2. 计算若，则停止计算，得近似解
3. 置
4. 一维搜索：求使得
5. 置
6. 计算
   1. 若，则停止计算，得近似解；
   2. 否则，按计算出
7. 置，转3.

BFGS

BFGS算法是最流行的拟牛顿算法。可以考虑用逼近海赛矩阵的逆矩阵，也可以考虑用逼近海赛矩阵。这时，相应的拟牛顿条件是

可以用同样的方法得到另一迭代公式。首先令

考虑使和满足：

找出适合条件的和，得到BFGS算法矩阵的迭代公式：

可以证明，如果初始矩阵是正定的，则迭代过程中的每个矩阵都是正定的。

输入：目标函数，梯度，精度要求；输出：的极小点

1. 选定初始点，取为正定对称矩阵，置
2. 计算若，则停止计算，得近似解
3. 由求出
4. 一维搜索：求使得
5. 置
6. 计算
   1. 若，则停止计算，得近似解
   2. 否则，按计算出
7. 置，转3.

坐标下降法(Coordinate descent)

坐标下降法是一种非梯度优化方法，它在每步迭代中沿一个坐标方向进行搜索，通过循环使用不用的坐标方向来达到目标函数的局部极小值。

假设我们求解的极小值，其中是一个维向量。从初始点开始，坐标下降法通过迭代地构造序列来解决问题，的第个分量构造为：

通过执行此操作，显然有

与梯度下降法类似，通过迭代执行该过程，序列能收敛到所期望的局部极小点或驻点。坐标下降法不需计算目标函数的梯度，在每次迭代中仅需求解一维搜索问题，对于某些复杂问题计算较为简便。但若目标函数不光滑，则坐标下降法有可能陷入非驻点。

最小二乘法(Least squares)

最小二乘法是无约束的数学优化方法，通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小，即

最小值可以通过对上式参数分别求偏导数，然后使它们等于零得到。

应用举例

某次实验得到了四个数据点：。我们希望找出一条和这四个点最匹配的直线，即找出在“最佳情况”下能够大致符合如下超定线性方程组的和：

最小二乘法采用的手段是尽量使得等号两边的方差最小，也就是找出这个函数的最小值：

最小值可以通过对分别求和的偏导数，然后使它们等于零得到。

如此就得到了一个只有两个未知数的方程组，易得，，所以最佳

置信域方法（Trust-region methods）

置信域方法（Trust-region methods）又称信赖域方法，它是一种最优化方法，能够保证最优化方法总体收敛。

思想框架

求，是定义在上的二阶连续可微函数。定义当前点邻域。这里称为置信域半径。假定在这个邻域中，二次模型是目标函数的一个合适的近似，则在这个邻域（称为置信域）中极小化二次模型，得到近似极小点，并取，其中。

置信域方法的模型子问题是

其中，，，是一个对称矩阵，它是Hessian矩阵或其近似，为置信域半径，为某一范数，通常我们采用L2范数。选择的方法：根据模型函数对目标函数的拟合程度来调整置信域半径。对于置信域方法的模型子问题的解，设目标函数的下降量

为实际下降量，设模型函数的下降量

为预测下降量。定义比值

它用来衡量模型函数与目标函数的一致性程度。

具体算法

1. 给出初始点，置信域半径的上界，，，，，
2. 如果，停止
3. (近似地)求解置信域方法的模型子问题，得到
4. 计算和。令
   1. 
5. 校正置信域半径，令
   1. 
6. 产生，校正，令，转2.