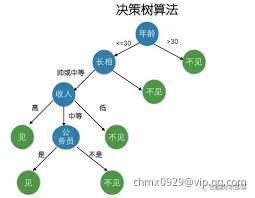
决策树是一种自上而下,对样本进行树形分类的过程,由结点和有向边组成。结点分为内部结点和叶结点,每个内部结点表示一个特征或属性,叶结点表示类别。从顶部根节点开始,所有样本聚在一起。经过根节点的划分,样本被分到不同的子结点中。再根据子结点的特征进一步划分,直至所有样本都被归到某一个类别(即叶结点)中。
输入:训练集,属性集
过程:函数TreeGenerate(D, A)
生成结点node;if D中样本全属于同一类别C将node标记为C类叶结点;returnif A为空或D中样本在A上取值相同将node标记为叶结点,其类别标记为D中样本最多的类;return从A中选择较优划分属性afor a的每一个值v为node生成一个分支;令Dv表示D在a上取值为v的样本子集if Dv为空将分支结点标记为叶结点,其类别标记为D中样本最多的类;returnelse以TreeGenerate(Dv,A\a)为分支结点
输出:以node为根结点的一颗决策树
显然,决策树的生成是一个递归过程,在决策树算法中,有三种情形会导致递归返回:
- 当前结点包含的样本全属于同一类别,无需划分
- 当前结点属性集为空,或是所有样本在所有属性上取值相同,无法划分
- 当前结点包含的样本集合为空,不能划分
这里情形2.是在是在利用当前结点的后验分布,情形3则是把父结点的样本分布作为当前结点的先验分布
模型与划分
从决策树学习的逻辑可以看出,第8行和第10行,即如何找到最优划分属性和这个属性的最优划分点最为关键。随着划分不断进行,我们希望决策树的分支结点所包含的样本尽可能属于同一类别,即结点的”纯度“越来越高。
从样本类型的角度,ID3只能处理离散型变量,而C4.5和CART都可以处理连续型变量。C4.5处理连续型变量时,通过对数据排序之后找到类别不同的切割线作为切分点,根据切分点把连续属性转化为布尔型,从而将连续型变量转换多个取值区间的离散型变量。CART由于构建时每次都会对特征进行二值划分,因此可以很好地适用于连续型变量。
从应用角度,ID3和C4.5只能用于分类任务,而CART(Classification and Regression Tree)不仅可以用于分类,还可以应用于回归任务。
从其他角度,ID3对样本特征缺失值敏感,而C4.5和CART可以对缺失值进行不同方式的处理;ID3和C4.5可以在每个结点上产生出多叉分支,且每个特征在层级之间不会复用,而CART每个结点只会产生两个分支(二叉树),且每个特征可以被重复使用;ID3和C4.5通过剪枝来权衡树的准确性和泛化能力,而CART直接利用全部数据发现所有可能的树结构进行对比。
| ID3 | C4.5 | CART | |
|---|---|---|---|
| 样本类型 | 离散 | 离散、连续 | 离散、连续 |
| 应用任务 | 分类 | 分类 | 分类、回归 |
| 缺失值 | 敏感 | 不敏感 | 不敏感 |
| 分支 | 多叉 | 多叉 | 二叉 |
| 特征复用 | 不复用 | 不复用 | 复用 |
| 提高泛化 | 剪枝 | 剪枝 | 利用数据优化结构 |
以下为三个模型举例数据(buys_computer为类别):
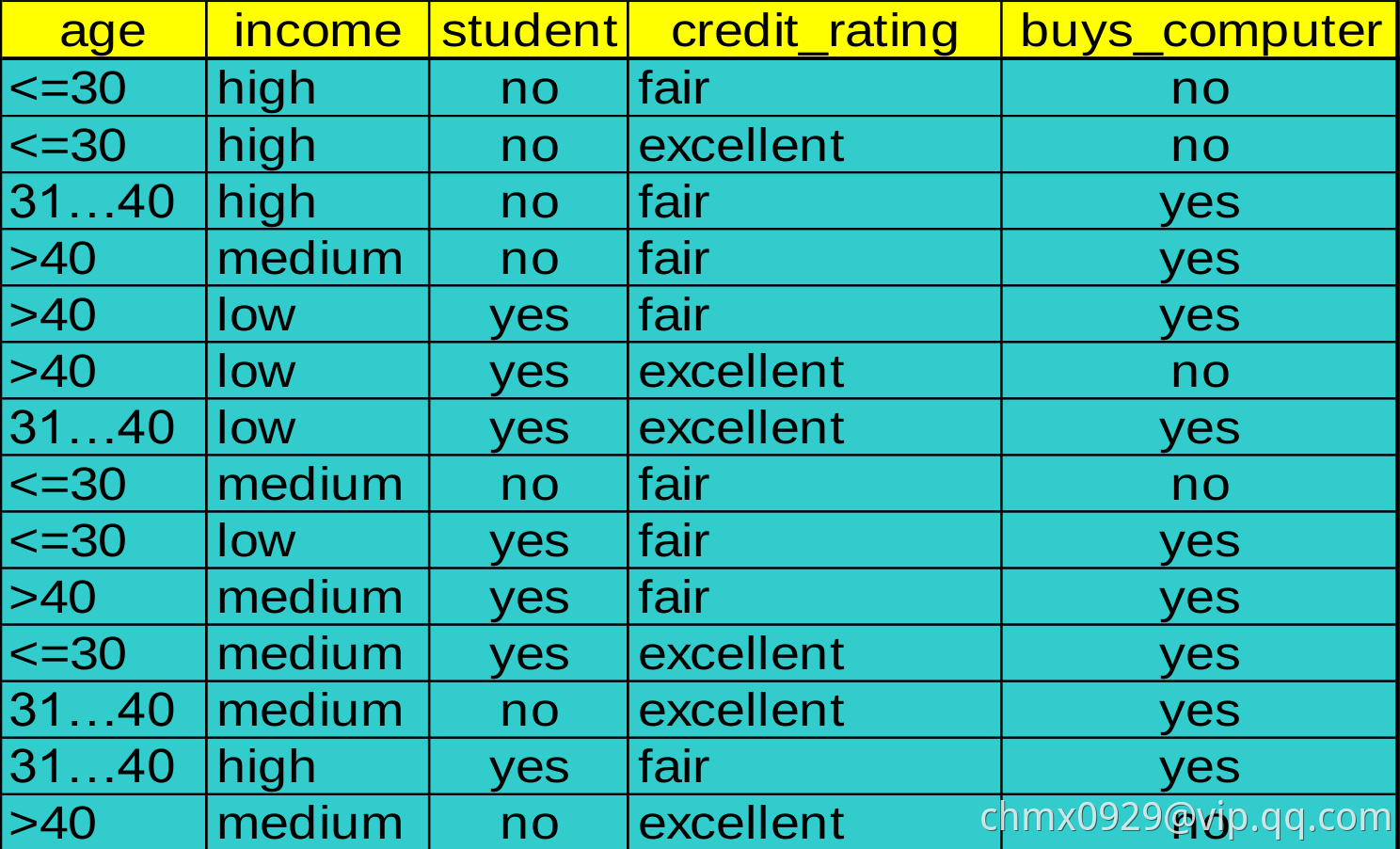
ID3 信息增益(Information Gain)
信息熵(信息熵越高说明不确定性越高)
是样本集合
中属于第
类的样本子集,
该子集的元素个数,
样本集合的元素个数:
经验条件熵(按特征A划分)
表示
中特征
取第
个值的样本子集,
表示
中属于第
类的样本子集:
信息增益(Information Gain)
示例
,
代表
的14个中有5个,且2个yes,3个no,同理剩下两项各代表4个
和5个
的样本
所以,,同理得
,
,
,
最高,所以按年龄划分
C4.5 增益率(Gain ratio)
ID3采用信息增益作为评价标准,会倾向于取值较多的特征。因为信息增益反应的是给定条件不确定性减少的程度,特征取值越多就意味着确定性高,也就是条件熵越小,信息增益越大。这在实际应用中是一个缺陷。比如我们引入“DNA”特征,每个人的“DNA”都不同,如果ID3按照“DNA”特征进行划分一定是最优的,但这种泛化能力非常弱。因此,C4.5实际上是对ID3进行优化,通过引入信息增益比,一定程度上对取值比较多的特征进行惩罚,避免ID3出现的过拟合的特性,提升决策树的泛化能力。
,其中
求得各特征增益率,选出信息增益率最大的特征进行切分
示例
CART 基尼指数(Gini index)
基尼指数描述数据的纯度,对于数据集,有
个类别的话,则:
CART的特征可以重复使用,每次只产生两个分支,设根据特征将数据集分为
和
,则:
求得各特征所有切分点的Gini index后,找到最小的进行切分
示例
,例子中有9个有电脑5个没有(类别)
按收入low,medium一组(10个样本在),high一组(4个在
)切分的话:
同理得各特征所有切分的Gini Index,找到最小的那个进行切分最优
剪枝处理
一颗完全生长的决策树很容易出现过拟合问题,除了常规的机器学习解决过拟合的方法外,我们可以对决策树进行剪枝,常用的剪枝方法有预剪枝(Pre-Pruning)和后剪枝(Post-Pruning)。
预剪枝
预剪枝的核心思想是在树中结点进行扩展之前,先计算当前的划分能否带来模型泛化能力的提升,如果不能,则不再继续生长子树。预剪枝对于何时停止决策树的生长有以下几种方法:
1、当树到达一定深度的时候,停止树的生长
2、当到达当前结点的样本数量小于某个阈值的时候,停止树的生长
3、计算每次分裂对测试集的准确度提升,当小于某个阈值的时候,不再继续拓展
预剪枝具有思想直接、算法简单、效率高等特点,适合解决大规模问题。但如何准确地估计何时停止树的生长(即上述方法中的深度或阈值),针对不同问题会有很大差别,需要一定经验判断。且预剪枝存在一定局限性,有欠拟合风险,虽然当前的划分会导致测试集准确率降低,但在之后的划分中,准确率可能会有显著上升。
后剪枝
后剪枝的核心思想是让算法生成一颗完全生长的决策树,然后从最底层向上计算是否剪枝。剪枝过程将子树删除,用一个叶子结点替代,该节点的类别按多数投票原则进行判断。同样地,后剪枝也可以通过在测试集上的准确率进行判断,如果剪枝过后准确率有所提升,则进行剪枝。相比于预剪枝,后剪枝方法通常可以得到泛化能力更强的决策树,但时间开销会更大。
常见的后剪枝方法包括错误率降低剪枝 (Reduced Error Pruning, REP),悲观剪枝(Pessimistic Error Pruning, PEP)、代价复杂度剪枝(Cost Complexity Pruning, CCP)、最小误差剪枝(Minimum Error Pruning, MEP)、CVP(Critical Value Pruning)、OPP(Optimal Pruning)。
Code实现
三种:ID3(基于信息增益)C4.5(基于信息增益比)CART(Gini指数)
Entropy:
Conditional entropy:
Information gain:
Information gain ratio:
Gini index:
数据取值《统计学习方法(第1版))》(李航)书上题目5.1
数据
import numpy as npimport pandas as pdimport matplotlib.pyplot as plt%matplotlib inlinefrom sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_splitfrom collections import Counterimport mathfrom math import logimport pprint# 书上题目5.1def create_data():datasets = [['青年', '否', '否', '一般', '否'],['青年', '否', '否', '好', '否'],['青年', '是', '否', '好', '是'],['青年', '是', '是', '一般', '是'],['青年', '否', '否', '一般', '否'],['中年', '否', '否', '一般', '否'],['中年', '否', '否', '好', '否'],['中年', '是', '是', '好', '是'],['中年', '否', '是', '非常好', '是'],['中年', '否', '是', '非常好', '是'],['老年', '否', '是', '非常好', '是'],['老年', '否', '是', '好', '是'],['老年', '是', '否', '好', '是'],['老年', '是', '否', '非常好', '是'],['老年', '否', '否', '一般', '否'],]labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别']# 返回数据集和每个维度的名称return datasets, labelsdatasets, labels = create_data()train_data = pd.DataFrame(datasets, columns=labels)
手写实现
# 熵def calc_ent(datasets):data_length = len(datasets)label_count = {}for i in range(data_length):label = datasets[i][-1]if label not in label_count:label_count[label] = 0label_count[label] += 1ent = -sum([(p/data_length)*log(p/data_length, 2) for p in label_count.values()])return ent# 经验条件熵def cond_ent(datasets, axis=0):data_length = len(datasets)feature_sets = {}for i in range(data_length):feature = datasets[i][axis]if feature not in feature_sets:feature_sets[feature] = []feature_sets[feature].append(datasets[i])cond_ent = sum([(len(p)/data_length)*calc_ent(p) for p in feature_sets.values()])return cond_ent# 信息增益def info_gain(ent, cond_ent):return ent - cond_entdef info_gain_train(datasets):count = len(datasets[0]) - 1ent = calc_ent(datasets)best_feature = []for c in range(count):c_info_gain = info_gain(ent, cond_ent(datasets, axis=c))best_feature.append((c, c_info_gain))print('特征({}) - info_gain - {:.3f}'.format(labels[c], c_info_gain))# 比较大小best_ = max(best_feature, key=lambda x: x[-1])return '特征({})的信息增益最大,选择为根节点特征'.format(labels[best_[0]])info_gain_train(np.array(datasets))
# 定义节点类 二叉树class Node:def __init__(self, root=True, label=None, feature_name=None, feature=None):self.root = rootself.label = labelself.feature_name = feature_nameself.feature = featureself.tree = {}self.result = {'label:': self.label, 'feature': self.feature, 'tree': self.tree}def __repr__(self):return '{}'.format(self.result)def add_node(self, val, node):self.tree[val] = nodedef predict(self, features):if self.root is True:return self.labelreturn self.tree[features[self.feature]].predict(features)class DTree:def __init__(self, epsilon=0.1):self.epsilon = epsilonself._tree = {}# 熵@staticmethoddef calc_ent(datasets):data_length = len(datasets)label_count = {}for i in range(data_length):label = datasets[i][-1]if label not in label_count:label_count[label] = 0label_count[label] += 1ent = -sum([(p/data_length)*log(p/data_length, 2) for p in label_count.values()])return ent# 经验条件熵def cond_ent(self, datasets, axis=0):data_length = len(datasets)feature_sets = {}for i in range(data_length):feature = datasets[i][axis]if feature not in feature_sets:feature_sets[feature] = []feature_sets[feature].append(datasets[i])cond_ent = sum([(len(p)/data_length)*self.calc_ent(p) for p in feature_sets.values()])return cond_ent# 信息增益@staticmethoddef info_gain(ent, cond_ent):return ent - cond_entdef info_gain_train(self, datasets):count = len(datasets[0]) - 1ent = self.calc_ent(datasets)best_feature = []for c in range(count):c_info_gain = self.info_gain(ent, self.cond_ent(datasets, axis=c))best_feature.append((c, c_info_gain))# 比较大小best_ = max(best_feature, key=lambda x: x[-1])return best_def train(self, train_data):"""input:数据集D(DataFrame格式),特征集A,阈值etaoutput:决策树T"""_, y_train, features = train_data.iloc[:, :-1], train_data.iloc[:, -1], train_data.columns[:-1]# 1,若D中实例属于同一类Ck,则T为单节点树,并将类Ck作为结点的类标记,返回Tif len(y_train.value_counts()) == 1:return Node(root=True,label=y_train.iloc[0])# 2, 若A为空,则T为单节点树,将D中实例树最大的类Ck作为该节点的类标记,返回Tif len(features) == 0:return Node(root=True, label=y_train.value_counts().sort_values(ascending=False).index[0])# 3,计算最大信息增益 同5.1,Ag为信息增益最大的特征max_feature, max_info_gain = self.info_gain_train(np.array(train_data))max_feature_name = features[max_feature]# 4,Ag的信息增益小于阈值eta,则置T为单节点树,并将D中是实例数最大的类Ck作为该节点的类标记,返回Tif max_info_gain < self.epsilon:return Node(root=True, label=y_train.value_counts().sort_values(ascending=False).index[0])# 5,构建Ag子集node_tree = Node(root=False, feature_name=max_feature_name, feature=max_feature)feature_list = train_data[max_feature_name].value_counts().indexfor f in feature_list:sub_train_df = train_data.loc[train_data[max_feature_name] == f].drop([max_feature_name], axis=1)# 6, 递归生成树sub_tree = self.train(sub_train_df)node_tree.add_node(f, sub_tree)# pprint.pprint(node_tree.tree)return node_treedef fit(self, train_data):self._tree = self.train(train_data)return self._treedef predict(self, X_test):return self._tree.predict(X_test)datasets, labels = create_data()data_df = pd.DataFrame(datasets, columns=labels)dt = DTree()tree = dt.fit(data_df)treedt.predict(['老年', '否', '否', '一般'])
sklearn实现
https://sklearn.tree.DecisionTreeClassifier
from sklearn.tree import DecisionTreeClassifierfrom sklearn.tree import export_graphvizimport graphvizclf = DecisionTreeClassifier()clf.fit(X_train, y_train,)clf.score(X_test, y_test)clf.predict(X_test)

