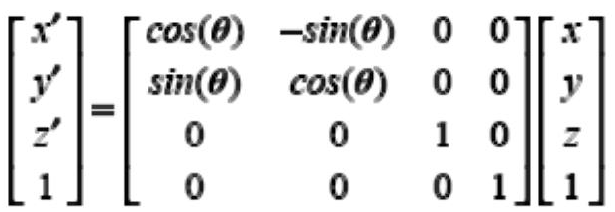2. Geometric Model of Camera

Perspective Projection:

Perspective Projection Equations:

Coordinate Rotation and Translation:

2D coordinate rotation and transformation: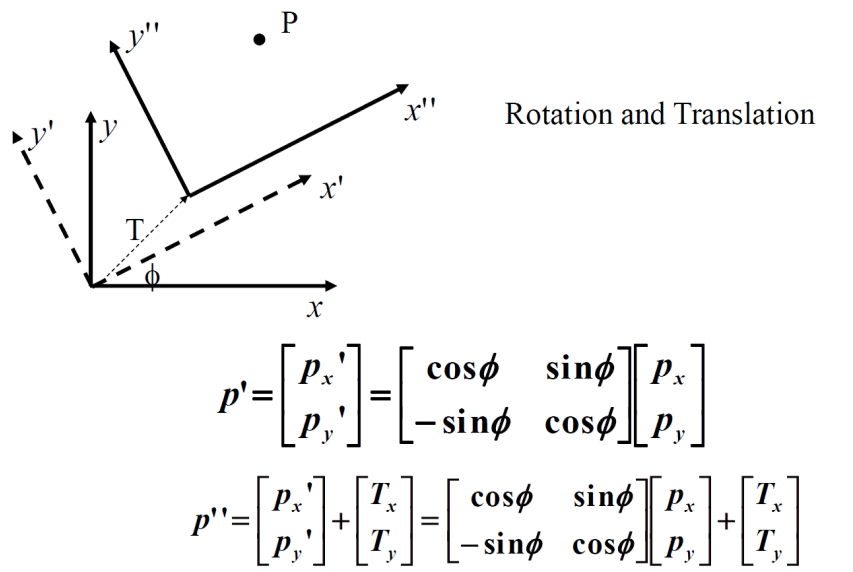

2D coordinate transformation using Homogeneous Coordinates: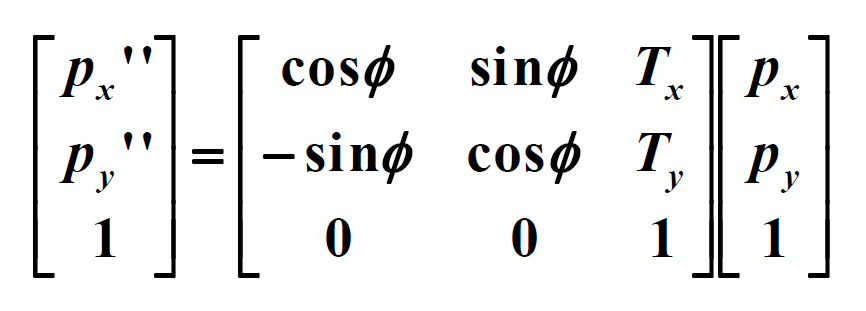

**

Homogeneous Coordinates:

translations with HC:

scalings with HC:

rotation with HC:

w:

• The distance from object to origin (or projector)

3D Rotation:

3D Rotation in homogeneous coordinates:

X-axis:

Y-axis:

Z-axis:

combine the 3 rotations:

inversions of 3D rotation matrix:

so that

Also,

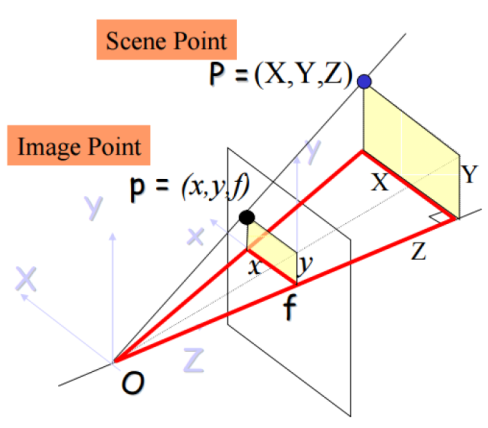
Perspective Projection:

2 methods:

• Transformation
  • N dim to N dim
• Projection
  • N dim to M dim

and we seek a transformation matrix in:

using homogenous coordinate, we have a linear relation:

so that

Perspective Projection Matrix:

(using homogeneous coordinates)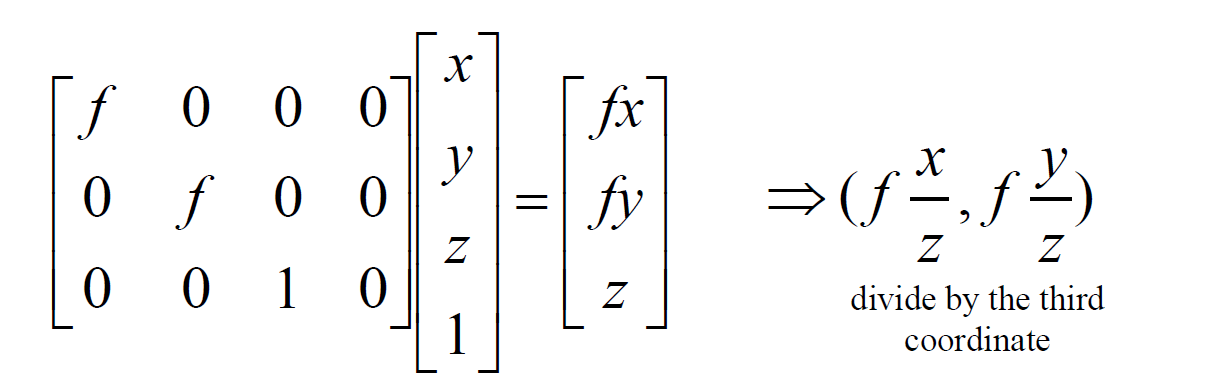

World to camera transformation:

Transform coordinations, R is based on from Pw to Pc.
(w = world, c = camera)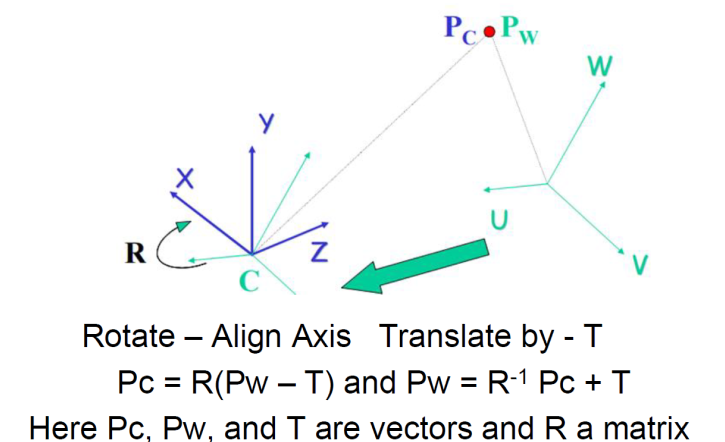

(Pc and Pw are from the same point)

World to Camera Coordinate Transformation Matrix:

R is 3D rotation matrix,
C is a vector of camera position in world frame

for example, this matrix looks like:

Then the corresponding transformation from world coordinates to camera coordinates is: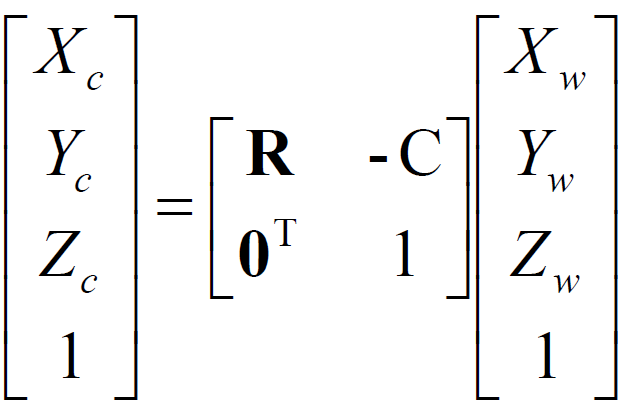

Camera Coordinates to Image Coordinates Matrix:

: pixel sizes in mm per pixel

and the camera calibration matrix is:

• x, y are in pixels, so are in millimeters/pixel
• f is in millimeters
• are in pixels

• Image co-ordinates are in pixels
• Camera co-ordinates are in millimetres

In/Extrinsic Parameters:

• Extrinsic parameters define the location and orientation of the world reference frame with respect to the camera reference frame
• Intrinsic parameters link pixel co-ordinates in the image with the corresponding co-ordinates in the camera reference frame

Parameters in K are intrinsic camera parameters.
[R -C] has extrinsic camera parameters.

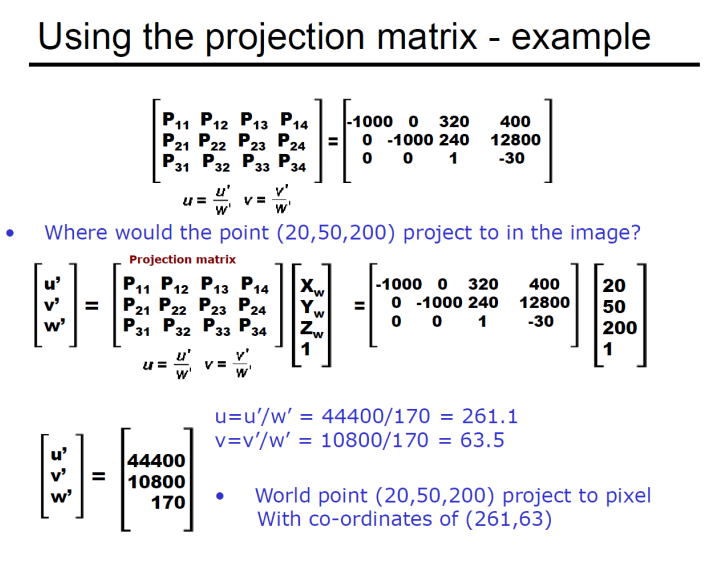
Projection matrix:

It maps 3d points to the appropriate image coordinates in pixels

example:

Weak Perspective Model / Orthography:

If the distance between any 2 points in an object is much smaller (1/20 at most) at most than the average distance of the object ()
The camera projection can be approximated as:

(simply is to approximate the coordinate with a approximate average Z value)
This method can simplify some mathematics.

Image distortion due to optics:

Radial Distortion:

depends on radius r, there is radial distortion from center of image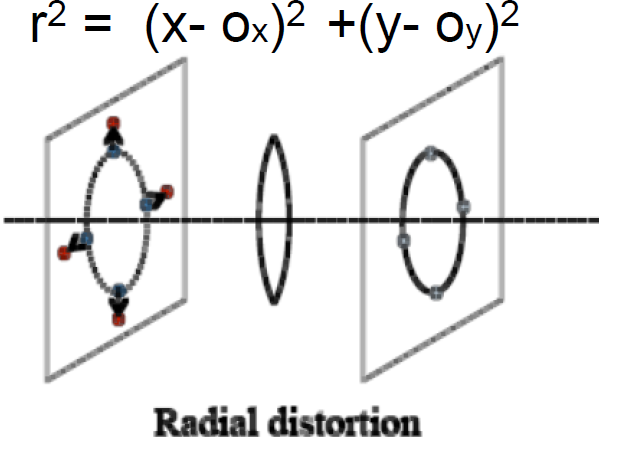

Error is proportional to distance of pixel from the camera center (the radius of the point)

Tangential Distortion:

(Ox, Oy) – center of projection is not the center of image

Reference:

• wikipedia
• https://www.tomdalling.com/blog/modern-opengl/explaining-homogenous-coordinates-and-projective-geometry/
• handout of COMP4102: Introduction to Computer Vision from Carleton University School of Computer Science, 2019