6. Homography

Linear Mapping / Transformation:

• Includes different types of transformations from a given 2d image to another 2d image
• a 2d perspective transformation is commonly called an image warp or a homography
• Input a 2d image, output another 2d image
  • map points from a pixel in source image to a pixel destination

Homography = Linear warp:

• We have
  • pixel
  • homography
• and the mapped pixel is
  • apply this to all pixels would get a warped version of the original image
• Also,
• it’s a one-to-one transform
  • image projection is many-to-one

Homography conditions:

• 3 camera images are related by a homography iff:
  • both images see the same plane but from a different angle and possibly different position

OR

• both images are taken from a camera at the same position but from a different angle
  • it’s independent to what the cameras are looking at

Case 1: 2 camera views of the same plane:

• P is the point on the plane
• 2 views “a” “b”
• ,
• 

Case 2: rotating camera:

• 
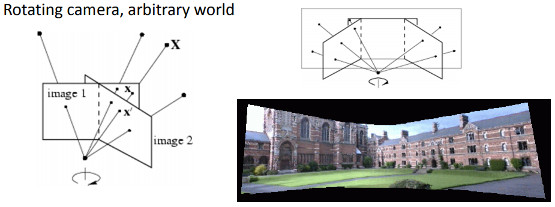
  • K is camera calibration matrix
  • R is rotation matrix

2D image transformations:

• Euclidean = Rigid

The 4 point algorithm:

• We need at least 4 points to compute M
• Obtain estimate M by eigenvector with smallest eigenvalue

  Recover Homography matrix from correspondences:

  
  

  Image Rectification:

  
  u = x, v = y
  u11, v11, u12, v12, u13, v13, u14, v14 are points from input picture.
  u21, v21, u22, v22, u23, v23, u24, v24 are corresponding points from warped picture.

Image Mosaics:

• blending of a group of images and gives a new larger image
• rotating a camera on a tripod can finish this
  • only the original image is not warped

• an application: panorama

Reference:

• wikipedia
• handout of COMP4102: Introduction to Computer Vision from Carleton University School of Computer Science, 2019