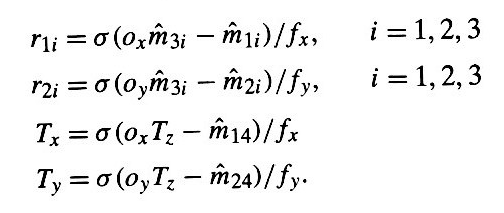8. Camera Calibration

EXIF:

Full name is Exchangeable Image File Format

• .JPG
• .TIF
• .WAV

EXIF tag include information of the camera and photo

• Date and time information
• Camera settings
• A thumbnail (picture as icon)
• Descriptions
• Copyright information

Find intrinsic camera parameters:

• EXIF has focal length f (in millimeters)
• camera manual has pixel size

Camera calibration:

Purpose:

• to determine geometric parameters of the image formation process

  Explicit camera calibration:

• Use a calibration object with a known geometry

• Write equations linking co-ordinates of the projected points,

and the camera parameters

• From images of the calibration target
  • Intrinsic camera parameters
    • (depend only on camera characteristics)
  • Extrinsic camera parameters
    • (depend only on position camera)
  • In OpenCV, the calibration process finds fx, fy, ox, oy, along with the distortion parameters

Methods:

1. Direct Approach (Tsai method)

• Write projection equations in terms of all the parameters
  • That is all the unknown intrinsic and extrinsic parameters
• Solve for these parameters using non-linear equations

1. Projection Matrix Approach

• Compute the projection matrix (the 3x4 matrix M)
• Compute camera parameters as closed-form functions of M

both approaches work with same data, but the direct approach requires an extra step

All calibration methods:

• Use patterns with know geometry or shape
• Take multiple views of theses patterns
• Match the information across the different views

Camera Parameters:

Intrinsic parameters (K matrix):

• Focal length f
• Pixel size in x and y directions: sx & sy

• Principal point ox & oy

  Extrinsic parameters ([R | T] matrix):

• Rotation matrix R

• Translation matrix T

  Projection matrix:

  P = K [R | T]
  (3 by 4 matrix)
  
  

• and the relationship between a image pixel and it’s corresponding world pixel is:

estimating the projection matrix:

solve Ax = 0 system with SVD

Decompose project matrix:

• Find scale by using unit vector
  • 
• Divide computed M by to get a new M matrix
  • Then,

(i = 1, 2, 3)
with

• Taking the dot products of q3 with q1 and q2 we find

  
  

• Then fx and fy can be recovered:

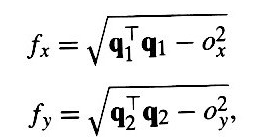
• and the rest of extrinsic parameters:

Reference:

• wikipedia
• handout of COMP4102: Introduction to Computer Vision from Carleton University School of Computer Science, 2019