上一章介绍了I/O设备的一般概念,并向您展示了操作系统如何与这样一个庞然大物交互。在这一章中,我们将更详细地介绍一种设备:硬盘驱动器。几十年来,这些驱动器一直是计算机系统中持久数据存储的主要形式,文件系统技术(即将到来)的许多发展都基于它们的行为。因此,在构建管理磁盘的文件系统软件之前,有必要了解磁盘操作的详细信息。许多细节都可以在Ruemmler和Wilkes [RW92]以及Anderson、Dykes和Riedel [ADR03]的优秀论文中找到。
关键的问题:如何存储和访问磁盘上的数据 现代硬盘驱动器如何存储数据?接口是什么?数据实际上是如何布局和访问的?磁盘调度如何提高性能?
37.1 接口 The Interface
让我们从了解现代磁盘驱动器的接口开始。所有现代驱动器的基本接口都很简单。驱动器由大量扇区(sectors)(512字节块)组成,每个扇区都可以被读或写。在有n个扇区的硬盘上,扇区的编号为0 ~ n - 1。因此,我们可以将磁盘看作扇区的数组;因此0到n - 1是驱动器的地址空间(address space)。
可以进行多扇区操作; 实际上,许多文件系统一次会读取或写入 4KB(或更多)。 但是,在更新磁盘时,驱动器制造商所做的唯一保证是单个 512 字节写入是原子的(atomic)(即,它将完全完成或根本不会完成); 因此,如果发生过早断电,则只能完成较大写入的一部分(有时称为撕裂写入(torn writes。译注:就是一次不完整的写入))。
大多数磁盘驱动器的客户端都会做一些假设,但这些假设并没有在接口中直接指定;Schlosser和Ganger将此称为磁盘驱动器的“不成文合同”[SG04]。具体来说,人们通常可以假设访问驱动器地址空间中两个彼此接近的块将比访问两个相距较远的块更快。人们通常也可以假设访问连续块中的块(即连续读或写)是最快的访问模式,通常比任何更多的随机访问模式快得多。
我们和其他人经常交替使用术语块和扇区(block and sector),假设读者知道每个上下文的确切含义。抱歉!
37.2 基本几何 Basic Geometry
让我们开始了解现代磁盘的一些组成部分。我们从一个盘片(platter)开始,这是一个圆形的硬表面,通过诱导磁变化,数据被持久地存储在上面。一个磁盘可以有一个或多个盘片; 每个盘片都有两侧(sides),每侧都叫做面(surface)。这些盘片通常由一些硬材料(如铝)制成,然后涂上一层薄磁性层,使驱动器即使在驱动器断电时也能持续存储比特(bits)。
盘片都捆绑在一起围绕主轴(spindle),主轴连接到一个电机,以一个恒定的(固定的)速率旋转盘片(当驱动器上电时)。转速通常以每分钟的转速(rotations per minute,RPM)来衡量,现代的典型值在 7,200 RPM 到 15,000 RPM 之间。请注意,我们通常会对单次旋转的时间感兴趣,例如,一个驱动器以 10,000 RPM 旋转意味着单次旋转大约需要6毫秒(6毫秒)。
数据被编码在扇区的同心圆上; 我们把这样的同心圆称为磁道(track)。一个表面包含成千上万的磁道,紧密地排列在一起,数百条磁道的宽度相当于一根头发的宽度。
要从表面进行读写,我们需要一种机制,让我们既可以感知(即读取)磁盘上的磁模式,也可以诱导(即写入)它们的变化。这个读写过程是由磁头(disk head)完成的; 驱动器的每个面(surface)都有一个这样的磁头。磁头连接到一个单一的磁头臂(disk arm)上,该磁头臂在面上移动来将磁头定位在所需的磁道上。
37.3 一个简单的磁盘驱动器 A Simple Disk Drive
让我们通过一次建立一个磁道的模型来了解磁盘的工作原理。 假设我们有一个单磁道的简单磁盘(图 37.1)。 该磁道只有 12 个扇区,每个扇区的大小为 512 字节(我们的典型扇区大小,回想一下),因此由数字 0 到 11 寻址。我们这里的单盘围绕主轴旋转,电机连接到主轴 。
Figure 37.1: A Disk With Just A Single Track
当然,这条磁道本身并不有趣; 我们希望能够读或写这些扇区,因此我们需要一个磁头,连接到磁头臂,正如我们现在看到的(图37.2)。在图中,磁头附在磁头臂的末端,定位在扇区6上,表面逆时针旋转。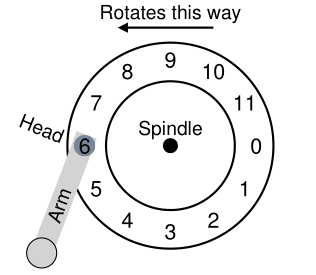
Figure 37.2: A Single Track Plus A Head
单磁道延迟:旋转延迟 Single-track Latency: The Rotational Delay
为了理解如何在简单的单磁道磁盘上处理请求,假设我们现在接收到一个读取块0的请求。磁盘应该如何处理这个请求?
在我们的简单磁盘中,磁盘不需要做很多事情。特别是,它必须等待所需扇区旋转到磁头下方。这种等待在现代驱动器中经常发生,并且是I/O服务时间的一个非常重要的组成部分,因此它有一个特殊的名称: 旋转延迟(rotational delay)(有时旋转延迟(rotation delay),尽管听起来很奇怪)。在这个例子中, 如果完整旋转延迟为 R,则磁盘必须产生大约 R/2 的旋转延迟,以等待 0 进入读/写磁头(如果我们从 6 开始)。 在这条单磁道上的最坏情况请求将是扇区 5,这会导致几乎完整的旋转延迟,以便为此类请求提供服务。
多磁道:寻道时间 Multiple Tracks: Seek Time
到目前为止,我们的磁盘只有一个单磁道,这不是太现实; 现代磁盘当然有数百万磁道。因此,让我们看看一个更加真实的磁盘表面,它有三个磁道(图37.3,左)。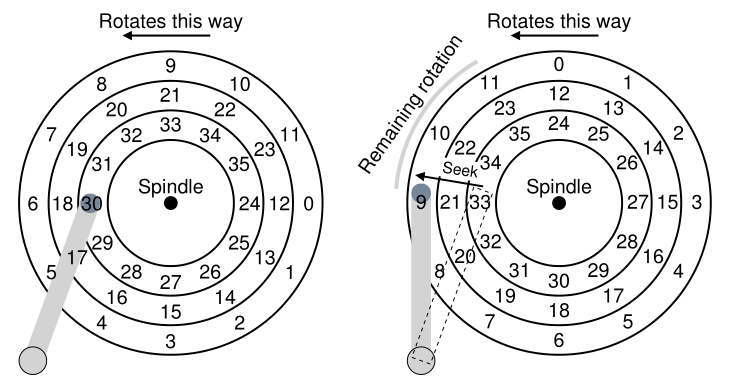
Figure 37.3: Three Tracks Plus A Head (Right: With Seek)
在图中,磁头目前位于最内层轨道上(包含扇区24到35); 下一个磁道包含下一组扇区(12 到 23),最外面的磁道包含第一组扇区(0 到 11)。
为了理解驱动器如何访问给定扇区,我们现在跟踪对较远扇区的请求会发生什么,例如读取扇区 11。要处理这个读取,驱动器必须首先将磁头臂移动到正确的磁道(在本例中是最外面的磁道),这个过程称为寻道(seek)。寻道和旋转延迟是成本最高的磁盘操作之一。
需要注意的是,寻道有很多阶段:首先是磁头臂运动时的加速度阶段; 然后当磁头臂全速移动时滑行,然后当磁头臂减速时减速; 最后,当磁头被小心地定位在正确的轨道上时,就稳定下来了。稳定时间(settling time)通常是相当重要的,例如0.5到2毫秒,因为驱动器必须确定找到正确的轨道(想象一下,如果它只是靠近!)。
搜索后,磁头臂已经将磁头定位在正确的轨道上。图37.3(右)对寻道的描述。
正如我们所看到的,在寻道过程中,磁头臂已经移动到想要的轨道上,而且盘片当然已经旋转了,在这种情况下大约旋转了3个扇区。因此,扇区 9 即将通过磁头下方,我们只需要忍受短暂的旋转延迟即可完成传输。
当扇区11通过磁头下面时,将发生I/O的最后阶段,即所谓的传输(transfer),在此期间,从磁盘表面读取或写入数据。这样,我们就有了一个完整的I/O时间图: 首先是寻道,然后等待旋转延迟,最后是传输。
一些其他细节 Some Other Details
虽然我们不会在这上面花太多时间,但是关于硬盘如何运行还有一些其他有趣的细节。许多驱动器使用某种磁道偏斜(track skew),以确保即使在跨越磁道边界时也能正确处理顺序读取。在我们的简单示例磁盘中,这可能如图37.4所示。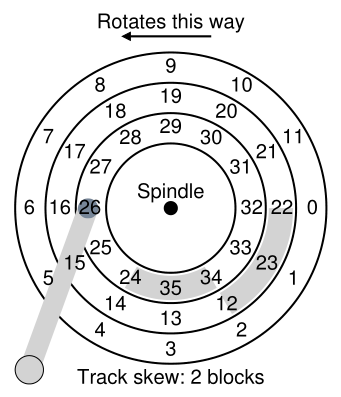
Figure 37.4: Three Tracks: Track Skew Of 2
扇区经常像这样偏斜,因为当从一个磁道切换到另一个磁道时,磁盘需要时间来重新定位磁头(甚至到相邻磁道)。 如果没有这种偏斜,磁头将移动到下一个磁道,但所需的下一个块已经在磁头下方旋转,因此驱动器将不得不等待几乎整个旋转延迟才能访问下一个块。
另一个事实是,外磁道往往比内磁道有更多的扇区,这是几何形状的结果; 那里有更多的空间。 这些磁道通常称为多区磁盘(multi-zoned)驱动器,其中磁盘被组织成多个区,而一个区是表面上的一组连续磁道。 每个区域的每个磁道具有相同数量的扇区,外部区域的扇区数多于内部区域。
最后,任何现代磁盘驱动器的一个重要部分是其缓存(cache),出于历史原因有时称为磁道缓冲区(track buffer)。 这个缓存只是一小部分内存(通常大约 8 或 16 MB),驱动器可以用它来保存从磁盘读取或写入磁盘的数据。 例如,当从磁盘读取一个扇区时,驱动器可能决定读取该磁道上的所有扇区并将它们缓存在其内存中; 这样做允许驱动器快速响应对同一轨道的任何后续请求。
在写入时,驱动器有一个选择:它应该在将数据放入内存时确认写入已完成,还是在写入实际写到磁盘后? 前者称为回写(write back)缓存(或有时称为立即报告(immediate reporting)),后者称为直写(write through)。 回写缓存有时会使驱动器看起来更快,但可能很危险; 如果文件系统或应用程序要求数据以特定顺序写入磁盘以确保正确性,回写缓存可能会导致问题(阅读文件系统日志一章了解详细信息)。
Aside:量纲分析 还记得在化学课上,你是如何通过简单地设置单位使它们相互抵消来解决几乎所有问题的?这种化学魔法以量纲分析(dimensional analysis)这个冠冕堂皇的名字而为人所知,它在计算机系统分析中也很有用。 让我们举一个例子来看看量纲是如何工作的以及它为什么有用。 在这种情况下,假设您必须计算出磁盘单次旋转需要多长时间(以毫秒为单位)。 不幸的是,您只能获得磁盘的 RPM 或每分钟转数(rotations per minute)。 假设我们谈论的是 10K RPM 磁盘(即,它每分钟旋转 10,000 次)。 我们如何设置量纲分析,以便以毫秒为单位获得每次旋转的时间? 为了做到这一点,我们首先把期望的单位放在左边;在这种情况下,我们希望得到每次旋转的时间(以毫秒为单位),所以这正是我们所写的:
。然后我们写下我们知道的所有东西,确保在可能的地方消掉单位。首先,我们得到
(保持rotation在底部,因为他在(等式)左边),然后用
把分钟转换成秒,最后用
把秒转换为毫秒,最终结果如下(巧妙地消除了单位):
正如您从这个示例中所看到的,量纲分析使看似直观的内容变成了一个简单且可重复的过程。除了上面的RPM计算,它还可以用于定期的I/O分析。例如,你经常会被告知磁盘的传输速率,例如100 MB/秒,然后问你:传输一个512 KB的块需要多长时间(以毫秒为单位)?通过量纲分析,它很简单:
%7D%7B1%20%5C%20Request%7D%3D%5Ctfrac%7B512%20%5C%20KB%7D%7B1%20%5C%20Request%7D%20%5Ccdot%20%5Ctfrac%7B1%20%5C%20MB%7D%7B1024%20%5C%20KB%7D%20%5Ccdot%20%5Ctfrac%7B1%20%5C%20second%7D%7B100%20%5C%20MB%7D%20%5Ccdot%20%5Ctfrac%7B1000%20%5C%20ms%7D%7B1%20%5C%20second%7D%20%3D%5Ctfrac%7B5%20%5C%20ms%7D%7B1%20%5C%20Request%7D%3C%2Ftitle%3E%0A%3Cdefs%20aria-hidden%3D%22true%22%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-54%22%20d%3D%22M40%20437Q21%20437%2021%20445Q21%20450%2037%20501T71%20602L88%20651Q93%20669%20101%20677H569H659Q691%20677%20697%20676T704%20667Q704%20661%20687%20553T668%20444Q668%20437%20649%20437Q640%20437%20637%20437T631%20442L629%20445Q629%20451%20635%20490T641%20551Q641%20586%20628%20604T573%20629Q568%20630%20515%20631Q469%20631%20457%20630T439%20622Q438%20621%20368%20343T298%2060Q298%2048%20386%2046Q418%2046%20427%2045T436%2036Q436%2031%20433%2022Q429%204%20424%201L422%200Q419%200%20415%200Q410%200%20363%201T228%202Q99%202%2064%200H49Q43%206%2043%209T45%2027Q49%2040%2055%2046H83H94Q174%2046%20189%2055Q190%2056%20191%2056Q196%2059%20201%2076T241%20233Q258%20301%20269%20344Q339%20619%20339%20625Q339%20630%20310%20630H279Q212%20630%20191%20624Q146%20614%20121%20583T67%20467Q60%20445%2057%20441T43%20437H40Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-69%22%20d%3D%22M184%20600Q184%20624%20203%20642T247%20661Q265%20661%20277%20649T290%20619Q290%20596%20270%20577T226%20557Q211%20557%20198%20567T184%20600ZM21%20287Q21%20295%2030%20318T54%20369T98%20420T158%20442Q197%20442%20223%20419T250%20357Q250%20340%20236%20301T196%20196T154%2083Q149%2061%20149%2051Q149%2026%20166%2026Q175%2026%20185%2029T208%2043T235%2078T260%20137Q263%20149%20265%20151T282%20153Q302%20153%20302%20143Q302%20135%20293%20112T268%2061T223%2011T161%20-11Q129%20-11%20102%2010T74%2074Q74%2091%2079%20106T122%20220Q160%20321%20166%20341T173%20380Q173%20404%20156%20404H154Q124%20404%2099%20371T61%20287Q60%20286%2059%20284T58%20281T56%20279T53%20278T49%20278T41%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-6D%22%20d%3D%22M21%20287Q22%20293%2024%20303T36%20341T56%20388T88%20425T132%20442T175%20435T205%20417T221%20395T229%20376L231%20369Q231%20367%20232%20367L243%20378Q303%20442%20384%20442Q401%20442%20415%20440T441%20433T460%20423T475%20411T485%20398T493%20385T497%20373T500%20364T502%20357L510%20367Q573%20442%20659%20442Q713%20442%20746%20415T780%20336Q780%20285%20742%20178T704%2050Q705%2036%20709%2031T724%2026Q752%2026%20776%2056T815%20138Q818%20149%20821%20151T837%20153Q857%20153%20857%20145Q857%20144%20853%20130Q845%20101%20831%2073T785%2017T716%20-10Q669%20-10%20648%2017T627%2073Q627%2092%20663%20193T700%20345Q700%20404%20656%20404H651Q565%20404%20506%20303L499%20291L466%20157Q433%2026%20428%2016Q415%20-11%20385%20-11Q372%20-11%20364%20-4T353%208T350%2018Q350%2029%20384%20161L420%20307Q423%20322%20423%20345Q423%20404%20379%20404H374Q288%20404%20229%20303L222%20291L189%20157Q156%2026%20151%2016Q138%20-11%20108%20-11Q95%20-11%2087%20-5T76%207T74%2017Q74%2030%20112%20181Q151%20335%20151%20342Q154%20357%20154%20369Q154%20405%20129%20405Q107%20405%2092%20377T69%20316T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-65%22%20d%3D%22M39%20168Q39%20225%2058%20272T107%20350T174%20402T244%20433T307%20442H310Q355%20442%20388%20420T421%20355Q421%20265%20310%20237Q261%20224%20176%20223Q139%20223%20138%20221Q138%20219%20132%20186T125%20128Q125%2081%20146%2054T209%2026T302%2045T394%20111Q403%20121%20406%20121Q410%20121%20419%20112T429%2098T420%2082T390%2055T344%2024T281%20-1T205%20-11Q126%20-11%2083%2042T39%20168ZM373%20353Q367%20405%20305%20405Q272%20405%20244%20391T199%20357T170%20316T154%20280T149%20261Q149%20260%20169%20260Q282%20260%20327%20284T373%20353Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-28%22%20d%3D%22M94%20250Q94%20319%20104%20381T127%20488T164%20576T202%20643T244%20695T277%20729T302%20750H315H319Q333%20750%20333%20741Q333%20738%20316%20720T275%20667T226%20581T184%20443T167%20250T184%2058T225%20-81T274%20-167T316%20-220T333%20-241Q333%20-250%20318%20-250H315H302L274%20-226Q180%20-141%20137%20-14T94%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-73%22%20d%3D%22M131%20289Q131%20321%20147%20354T203%20415T300%20442Q362%20442%20390%20415T419%20355Q419%20323%20402%20308T364%20292Q351%20292%20340%20300T328%20326Q328%20342%20337%20354T354%20372T367%20378Q368%20378%20368%20379Q368%20382%20361%20388T336%20399T297%20405Q249%20405%20227%20379T204%20326Q204%20301%20223%20291T278%20274T330%20259Q396%20230%20396%20163Q396%20135%20385%20107T352%2051T289%207T195%20-10Q118%20-10%2086%2019T53%2087Q53%20126%2074%20143T118%20160Q133%20160%20146%20151T160%20120Q160%2094%20142%2076T111%2058Q109%2057%20108%2057T107%2055Q108%2052%20115%2047T146%2034T201%2027Q237%2027%20263%2038T301%2066T318%2097T323%20122Q323%20150%20302%20164T254%20181T195%20196T148%20231Q131%20256%20131%20289Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-29%22%20d%3D%22M60%20749L64%20750Q69%20750%2074%20750H86L114%20726Q208%20641%20251%20514T294%20250Q294%20182%20284%20119T261%2012T224%20-76T186%20-143T145%20-194T113%20-227T90%20-246Q87%20-249%2086%20-250H74Q66%20-250%2063%20-250T58%20-247T55%20-238Q56%20-237%2066%20-225Q221%20-64%20221%20250T66%20725Q56%20737%2055%20738Q55%20746%2060%20749Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-31%22%20d%3D%22M213%20578L200%20573Q186%20568%20160%20563T102%20556H83V602H102Q149%20604%20189%20617T245%20641T273%20663Q275%20666%20285%20666Q294%20666%20302%20660V361L303%2061Q310%2054%20315%2052T339%2048T401%2046H427V0H416Q395%203%20257%203Q121%203%20100%200H88V46H114Q136%2046%20152%2046T177%2047T193%2050T201%2052T207%2057T213%2061V578Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-52%22%20d%3D%22M230%20637Q203%20637%20198%20638T193%20649Q193%20676%20204%20682Q206%20683%20378%20683Q550%20682%20564%20680Q620%20672%20658%20652T712%20606T733%20563T739%20529Q739%20484%20710%20445T643%20385T576%20351T538%20338L545%20333Q612%20295%20612%20223Q612%20212%20607%20162T602%2080V71Q602%2053%20603%2043T614%2025T640%2016Q668%2016%20686%2038T712%2085Q717%2099%20720%20102T735%20105Q755%20105%20755%2093Q755%2075%20731%2036Q693%20-21%20641%20-21H632Q571%20-21%20531%204T487%2082Q487%20109%20502%20166T517%20239Q517%20290%20474%20313Q459%20320%20449%20321T378%20323H309L277%20193Q244%2061%20244%2059Q244%2055%20245%2054T252%2050T269%2048T302%2046H333Q339%2038%20339%2037T336%2019Q332%206%20326%200H311Q275%202%20180%202Q146%202%20117%202T71%202T50%201Q33%201%2033%2010Q33%2012%2036%2024Q41%2043%2046%2045Q50%2046%2061%2046H67Q94%2046%20127%2049Q141%2052%20146%2061Q149%2065%20218%20339T287%20628Q287%20635%20230%20637ZM630%20554Q630%20586%20609%20608T523%20636Q521%20636%20500%20636T462%20637H440Q393%20637%20386%20627Q385%20624%20352%20494T319%20361Q319%20360%20388%20360Q466%20361%20492%20367Q556%20377%20592%20426Q608%20449%20619%20486T630%20554Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-71%22%20d%3D%22M33%20157Q33%20258%20109%20349T280%20441Q340%20441%20372%20389Q373%20390%20377%20395T388%20406T404%20418Q438%20442%20450%20442Q454%20442%20457%20439T460%20434Q460%20425%20391%20149Q320%20-135%20320%20-139Q320%20-147%20365%20-148H390Q396%20-156%20396%20-157T393%20-175Q389%20-188%20383%20-194H370Q339%20-192%20262%20-192Q234%20-192%20211%20-192T174%20-192T157%20-193Q143%20-193%20143%20-185Q143%20-182%20145%20-170Q149%20-154%20152%20-151T172%20-148Q220%20-148%20230%20-141Q238%20-136%20258%20-53T279%2032Q279%2033%20272%2029Q224%20-10%20172%20-10Q117%20-10%2075%2030T33%20157ZM352%20326Q329%20405%20277%20405Q242%20405%20210%20374T160%20293Q131%20214%20119%20129Q119%20126%20119%20118T118%20106Q118%2061%20136%2044T179%2026Q233%2026%20290%2098L298%20109L352%20326Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-75%22%20d%3D%22M21%20287Q21%20295%2030%20318T55%20370T99%20420T158%20442Q204%20442%20227%20417T250%20358Q250%20340%20216%20246T182%20105Q182%2062%20196%2045T238%2027T291%2044T328%2078L339%2095Q341%2099%20377%20247Q407%20367%20413%20387T427%20416Q444%20431%20463%20431Q480%20431%20488%20421T496%20402L420%2084Q419%2079%20419%2068Q419%2043%20426%2035T447%2026Q469%2029%20482%2057T512%20145Q514%20153%20532%20153Q551%20153%20551%20144Q550%20139%20549%20130T540%2098T523%2055T498%2017T462%20-8Q454%20-10%20438%20-10Q372%20-10%20347%2046Q345%2045%20336%2036T318%2021T296%206T267%20-6T233%20-11Q189%20-11%20155%207Q103%2038%20103%20113Q103%20170%20138%20262T173%20379Q173%20380%20173%20381Q173%20390%20173%20393T169%20400T158%20404H154Q131%20404%20112%20385T82%20344T65%20302T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-74%22%20d%3D%22M26%20385Q19%20392%2019%20395Q19%20399%2022%20411T27%20425Q29%20430%2036%20430T87%20431H140L159%20511Q162%20522%20166%20540T173%20566T179%20586T187%20603T197%20615T211%20624T229%20626Q247%20625%20254%20615T261%20596Q261%20589%20252%20549T232%20470L222%20433Q222%20431%20272%20431H323Q330%20424%20330%20420Q330%20398%20317%20385H210L174%20240Q135%2080%20135%2068Q135%2026%20162%2026Q197%2026%20230%2060T283%20144Q285%20150%20288%20151T303%20153H307Q322%20153%20322%20145Q322%20142%20319%20133Q314%20117%20301%2095T267%2048T216%206T155%20-11Q125%20-11%2098%204T59%2056Q57%2064%2057%2083V101L92%20241Q127%20382%20128%20383Q128%20385%2077%20385H26Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-3D%22%20d%3D%22M56%20347Q56%20360%2070%20367H707Q722%20359%20722%20347Q722%20336%20708%20328L390%20327H72Q56%20332%2056%20347ZM56%20153Q56%20168%2072%20173H708Q722%20163%20722%20153Q722%20140%20707%20133H70Q56%20140%2056%20153Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-35%22%20d%3D%22M164%20157Q164%20133%20148%20117T109%20101H102Q148%2022%20224%2022Q294%2022%20326%2082Q345%20115%20345%20210Q345%20313%20318%20349Q292%20382%20260%20382H254Q176%20382%20136%20314Q132%20307%20129%20306T114%20304Q97%20304%2095%20310Q93%20314%2093%20485V614Q93%20664%2098%20664Q100%20666%20102%20666Q103%20666%20123%20658T178%20642T253%20634Q324%20634%20389%20662Q397%20666%20402%20666Q410%20666%20410%20648V635Q328%20538%20205%20538Q174%20538%20149%20544L139%20546V374Q158%20388%20169%20396T205%20412T256%20420Q337%20420%20393%20355T449%20201Q449%20109%20385%2044T229%20-22Q148%20-22%2099%2032T50%20154Q50%20178%2061%20192T84%20210T107%20214Q132%20214%20148%20197T164%20157Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-32%22%20d%3D%22M109%20429Q82%20429%2066%20447T50%20491Q50%20562%20103%20614T235%20666Q326%20666%20387%20610T449%20465Q449%20422%20429%20383T381%20315T301%20241Q265%20210%20201%20149L142%2093L218%2092Q375%2092%20385%2097Q392%2099%20409%20186V189H449V186Q448%20183%20436%2095T421%203V0H50V19V31Q50%2038%2056%2046T86%2081Q115%20113%20136%20137Q145%20147%20170%20174T204%20211T233%20244T261%20278T284%20308T305%20340T320%20369T333%20401T340%20431T343%20464Q343%20527%20309%20573T212%20619Q179%20619%20154%20602T119%20569T109%20550Q109%20549%20114%20549Q132%20549%20151%20535T170%20489Q170%20464%20154%20447T109%20429Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-4B%22%20d%3D%22M285%20628Q285%20635%20228%20637Q205%20637%20198%20638T191%20647Q191%20649%20193%20661Q199%20681%20203%20682Q205%20683%20214%20683H219Q260%20681%20355%20681Q389%20681%20418%20681T463%20682T483%20682Q500%20682%20500%20674Q500%20669%20497%20660Q496%20658%20496%20654T495%20648T493%20644T490%20641T486%20639T479%20638T470%20637T456%20637Q416%20636%20405%20634T387%20623L306%20305Q307%20305%20490%20449T678%20597Q692%20611%20692%20620Q692%20635%20667%20637Q651%20637%20651%20648Q651%20650%20654%20662T659%20677Q662%20682%20676%20682Q680%20682%20711%20681T791%20680Q814%20680%20839%20681T869%20682Q889%20682%20889%20672Q889%20650%20881%20642Q878%20637%20862%20637Q787%20632%20726%20586Q710%20576%20656%20534T556%20455L509%20418L518%20396Q527%20374%20546%20329T581%20244Q656%2067%20661%2061Q663%2059%20666%2057Q680%2047%20717%2046H738Q744%2038%20744%2037T741%2019Q737%206%20731%200H720Q680%203%20625%203Q503%203%20488%200H478Q472%206%20472%209T474%2027Q478%2040%20480%2043T491%2046H494Q544%2046%20544%2071Q544%2075%20517%20141T485%20216L427%20354L359%20301L291%20248L268%20155Q245%2063%20245%2058Q245%2051%20253%2049T303%2046H334Q340%2037%20340%2035Q340%2019%20333%205Q328%200%20317%200Q314%200%20280%201T180%202Q118%202%2085%202T49%201Q31%201%2031%2011Q31%2013%2034%2025Q38%2041%2042%2043T65%2046Q92%2046%20125%2049Q139%2052%20144%2061Q147%2065%20216%20339T285%20628Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-42%22%20d%3D%22M231%20637Q204%20637%20199%20638T194%20649Q194%20676%20205%20682Q206%20683%20335%20683Q594%20683%20608%20681Q671%20671%20713%20636T756%20544Q756%20480%20698%20429T565%20360L555%20357Q619%20348%20660%20311T702%20219Q702%20146%20630%2078T453%201Q446%200%20242%200Q42%200%2039%202Q35%205%2035%2010Q35%2017%2037%2024Q42%2043%2047%2045Q51%2046%2062%2046H68Q95%2046%20128%2049Q142%2052%20147%2061Q150%2065%20219%20339T288%20628Q288%20635%20231%20637ZM649%20544Q649%20574%20634%20600T585%20634Q578%20636%20493%20637Q473%20637%20451%20637T416%20636H403Q388%20635%20384%20626Q382%20622%20352%20506Q352%20503%20351%20500L320%20374H401Q482%20374%20494%20376Q554%20386%20601%20434T649%20544ZM595%20229Q595%20273%20572%20302T512%20336Q506%20337%20429%20337Q311%20337%20310%20336Q310%20334%20293%20263T258%20122L240%2052Q240%2048%20252%2048T333%2046Q422%2046%20429%2047Q491%2054%20543%20105T595%20229Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-22C5%22%20d%3D%22M78%20250Q78%20274%2095%20292T138%20310Q162%20310%20180%20294T199%20251Q199%20226%20182%20208T139%20190T96%20207T78%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-4D%22%20d%3D%22M289%20629Q289%20635%20232%20637Q208%20637%20201%20638T194%20648Q194%20649%20196%20659Q197%20662%20198%20666T199%20671T201%20676T203%20679T207%20681T212%20683T220%20683T232%20684Q238%20684%20262%20684T307%20683Q386%20683%20398%20683T414%20678Q415%20674%20451%20396L487%20117L510%20154Q534%20190%20574%20254T662%20394Q837%20673%20839%20675Q840%20676%20842%20678T846%20681L852%20683H948Q965%20683%20988%20683T1017%20684Q1051%20684%201051%20673Q1051%20668%201048%20656T1045%20643Q1041%20637%201008%20637Q968%20636%20957%20634T939%20623Q936%20618%20867%20340T797%2059Q797%2055%20798%2054T805%2050T822%2048T855%2046H886Q892%2037%20892%2035Q892%2019%20885%205Q880%200%20869%200Q864%200%20828%201T736%202Q675%202%20644%202T609%201Q592%201%20592%2011Q592%2013%20594%2025Q598%2041%20602%2043T625%2046Q652%2046%20685%2049Q699%2052%20704%2061Q706%2065%20742%20207T813%20490T848%20631L654%20322Q458%2010%20453%205Q451%204%20449%203Q444%200%20433%200Q418%200%20415%207Q413%2011%20374%20317L335%20624L267%20354Q200%2088%20200%2079Q206%2046%20272%2046H282Q288%2041%20289%2037T286%2019Q282%203%20278%201Q274%200%20267%200Q265%200%20255%200T221%201T157%202Q127%202%2095%201T58%200Q43%200%2039%202T35%2011Q35%2013%2038%2025T43%2040Q45%2046%2065%2046Q135%2046%20154%2086Q158%2092%20223%20354T289%20629Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-30%22%20d%3D%22M96%20585Q152%20666%20249%20666Q297%20666%20345%20640T423%20548Q460%20465%20460%20320Q460%20165%20417%2083Q397%2041%20362%2016T301%20-15T250%20-22Q224%20-22%20198%20-16T137%2016T82%2083Q39%20165%2039%20320Q39%20494%2096%20585ZM321%20597Q291%20629%20250%20629Q208%20629%20178%20597Q153%20571%20145%20525T137%20333Q137%20175%20145%20125T181%2046Q209%2016%20250%2016Q290%2016%20318%2046Q347%2076%20354%20130T362%20333Q362%20478%20354%20524T321%20597Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-34%22%20d%3D%22M462%200Q444%203%20333%203Q217%203%20199%200H190V46H221Q241%2046%20248%2046T265%2048T279%2053T286%2061Q287%2063%20287%20115V165H28V211L179%20442Q332%20674%20334%20675Q336%20677%20355%20677H373L379%20671V211H471V165H379V114Q379%2073%20379%2066T385%2054Q393%2047%20442%2046H471V0H462ZM293%20211V545L74%20212L183%20211H293Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-63%22%20d%3D%22M34%20159Q34%20268%20120%20355T306%20442Q362%20442%20394%20418T427%20355Q427%20326%20408%20306T360%20285Q341%20285%20330%20295T319%20325T330%20359T352%20380T366%20386H367Q367%20388%20361%20392T340%20400T306%20404Q276%20404%20249%20390Q228%20381%20206%20359Q162%20315%20142%20235T121%20119Q121%2073%20147%2050Q169%2026%20205%2026H209Q321%2026%20394%20111Q403%20121%20406%20121Q410%20121%20419%20112T429%2098T420%2083T391%2055T346%2025T282%200T202%20-11Q127%20-11%2081%2037T34%20159Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-6F%22%20d%3D%22M201%20-11Q126%20-11%2080%2038T34%20156Q34%20221%2064%20279T146%20380Q222%20441%20301%20441Q333%20441%20341%20440Q354%20437%20367%20433T402%20417T438%20387T464%20338T476%20268Q476%20161%20390%2075T201%20-11ZM121%20120Q121%2070%20147%2048T206%2026Q250%2026%20289%2058T351%20142Q360%20163%20374%20216T388%20308Q388%20352%20370%20375Q346%20405%20306%20405Q243%20405%20195%20347Q158%20303%20140%20230T121%20120Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-6E%22%20d%3D%22M21%20287Q22%20293%2024%20303T36%20341T56%20388T89%20425T135%20442Q171%20442%20195%20424T225%20390T231%20369Q231%20367%20232%20367L243%20378Q304%20442%20382%20442Q436%20442%20469%20415T503%20336T465%20179T427%2052Q427%2026%20444%2026Q450%2026%20453%2027Q482%2032%20505%2065T540%20145Q542%20153%20560%20153Q580%20153%20580%20145Q580%20144%20576%20130Q568%20101%20554%2073T508%2017T439%20-10Q392%20-10%20371%2017T350%2073Q350%2092%20386%20193T423%20345Q423%20404%20379%20404H374Q288%20404%20229%20303L222%20291L189%20157Q156%2026%20151%2016Q138%20-11%20108%20-11Q95%20-11%2087%20-5T76%207T74%2017Q74%2030%20112%20180T152%20343Q153%20348%20153%20366Q153%20405%20129%20405Q91%20405%2066%20305Q60%20285%2060%20284Q58%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-64%22%20d%3D%22M366%20683Q367%20683%20438%20688T511%20694Q523%20694%20523%20686Q523%20679%20450%20384T375%2083T374%2068Q374%2026%20402%2026Q411%2027%20422%2035Q443%2055%20463%20131Q469%20151%20473%20152Q475%20153%20483%20153H487H491Q506%20153%20506%20145Q506%20140%20503%20129Q490%2079%20473%2048T445%208T417%20-8Q409%20-10%20393%20-10Q359%20-10%20336%205T306%2036L300%2051Q299%2052%20296%2050Q294%2048%20292%2046Q233%20-10%20172%20-10Q117%20-10%2075%2030T33%20157Q33%20205%2053%20255T101%20341Q148%20398%20195%20420T280%20442Q336%20442%20364%20400Q369%20394%20369%20396Q370%20400%20396%20505T424%20616Q424%20629%20417%20632T378%20637H357Q351%20643%20351%20645T353%20664Q358%20683%20366%20683ZM352%20326Q329%20405%20277%20405Q242%20405%20210%20374T160%20293Q131%20214%20119%20129Q119%20126%20119%20118T118%20106Q118%2061%20136%2044T179%2026Q233%2026%20290%2098L298%20109L352%20326Z%22%3E%3C%2Fpath%3E%0A%3C%2Fdefs%3E%0A%3Cg%20stroke%3D%22currentColor%22%20fill%3D%22currentColor%22%20stroke-width%3D%220%22%20transform%3D%22matrix(1%200%200%20-1%200%200)%22%20aria-hidden%3D%22true%22%3E%0A%3Cg%20transform%3D%22translate(120%2C0)%22%3E%0A%3Crect%20stroke%3D%22none%22%20width%3D%223567%22%20height%3D%2260%22%20x%3D%220%22%20y%3D%22220%22%3E%3C%2Frect%3E%0A%3Cg%20transform%3D%22translate(60%2C622)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-54%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22704%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%221050%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-65%22%20x%3D%221928%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%222748%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%223138%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%224016%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%224486%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(224%2C-429)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-52%22%20x%3D%22854%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-65%22%20x%3D%221613%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-71%22%20x%3D%222080%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%222540%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-65%22%20x%3D%223113%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%223579%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-74%22%20x%3D%224049%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%224085%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(5141%2C0)%22%3E%0A%3Cg%20transform%3D%22translate(120%2C0)%22%3E%0A%3Crect%20stroke%3D%22none%22%20width%3D%223238%22%20height%3D%2260%22%20x%3D%220%22%20y%3D%22220%22%3E%3C%2Frect%3E%0A%3Cg%20transform%3D%22translate(380%2C460)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-35%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-32%22%20x%3D%221001%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-4B%22%20x%3D%221855%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-42%22%20x%3D%222744%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(60%2C-429)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-52%22%20x%3D%22854%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-65%22%20x%3D%221613%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-71%22%20x%3D%222080%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%222540%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-65%22%20x%3D%223113%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%223579%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-74%22%20x%3D%224049%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-22C5%22%20x%3D%228842%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(9343%2C0)%22%3E%0A%3Cg%20transform%3D%22translate(120%2C0)%22%3E%0A%3Crect%20stroke%3D%22none%22%20width%3D%222951%22%20height%3D%2260%22%20x%3D%220%22%20y%3D%22220%22%3E%3C%2Frect%3E%0A%3Cg%20transform%3D%22translate(533%2C445)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-4D%22%20x%3D%22854%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-42%22%20x%3D%221905%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(60%2C-429)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-32%22%20x%3D%221001%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-34%22%20x%3D%221501%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-4B%22%20x%3D%222355%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-42%22%20x%3D%223245%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-22C5%22%20x%3D%2212757%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(13257%2C0)%22%3E%0A%3Cg%20transform%3D%22translate(120%2C0)%22%3E%0A%3Crect%20stroke%3D%22none%22%20width%3D%222830%22%20height%3D%2260%22%20x%3D%220%22%20y%3D%22220%22%3E%3C%2Frect%3E%0A%3Cg%20transform%3D%22translate(60%2C453)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%22854%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-65%22%20x%3D%221323%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-63%22%20x%3D%221790%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6F%22%20x%3D%222223%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%222709%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-64%22%20x%3D%223309%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(119%2C-429)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%221001%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-4D%22%20x%3D%221855%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-42%22%20x%3D%222906%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-22C5%22%20x%3D%2216550%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(17051%2C0)%22%3E%0A%3Cg%20transform%3D%22translate(120%2C0)%22%3E%0A%3Crect%20stroke%3D%22none%22%20width%3D%222830%22%20height%3D%2260%22%20x%3D%220%22%20y%3D%22220%22%3E%3C%2Frect%3E%0A%3Cg%20transform%3D%22translate(105%2C460)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%221001%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%221501%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%222355%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%223234%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(60%2C-436)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%22854%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-65%22%20x%3D%221323%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-63%22%20x%3D%221790%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6F%22%20x%3D%222223%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%222709%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-64%22%20x%3D%223309%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%2220399%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(21455%2C0)%22%3E%0A%3Cg%20transform%3D%22translate(120%2C0)%22%3E%0A%3Crect%20stroke%3D%22none%22%20width%3D%223238%22%20height%3D%2260%22%20x%3D%220%22%20y%3D%22220%22%3E%3C%2Frect%3E%0A%3Cg%20transform%3D%22translate(840%2C460)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-35%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%22854%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%221732%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(60%2C-429)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-52%22%20x%3D%22854%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-65%22%20x%3D%221613%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-71%22%20x%3D%222080%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%222540%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-65%22%20x%3D%223113%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%223579%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-74%22%20x%3D%224049%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=%5Ctfrac%7BTime%5C%20%28ms%29%7D%7B1%20%5C%20Request%7D%3D%5Ctfrac%7B512%20%5C%20KB%7D%7B1%20%5C%20Request%7D%20%5Ccdot%20%5Ctfrac%7B1%20%5C%20MB%7D%7B1024%20%5C%20KB%7D%20%5Ccdot%20%5Ctfrac%7B1%20%5C%20second%7D%7B100%20%5C%20MB%7D%20%5Ccdot%20%5Ctfrac%7B1000%20%5C%20ms%7D%7B1%20%5C%20second%7D%20%3D%5Ctfrac%7B5%20%5C%20ms%7D%7B1%20%5C%20Request%7D&id=izdgt)
37.4 I/O 时间:做数学 I/O Time: Doing The Math
现在我们已经有了磁盘的抽象模型,我们可以使用一些分析来更好地理解磁盘性能。特别地,我们现在可以将I/O时间表示为三个主要组件的总和:
请注意,I/O 速率 () 通常更容易用于驱动器之间的比较(如下文所述),很容易从时间计算出来。 只需将传输大小除以花费的时间:
为了更好地了解I/O时间,让我们执行以下计算。假设有两个我们感兴趣的工作负载。第一个称为随机(random)工作负载,向磁盘上的随机位置发出小的(例如4KB)读操作。随机工作负载在许多重要的应用程序中都很常见,包括数据库管理系统。第二种工作负载称为连续(sequential)工作负载,它只是从磁盘连续地读取大量扇区,而不是跳来跳去。连续访问模式非常常见,因此也很重要。
要了解随机工作负载和连续工作负载之间的性能差异,我们需要先对磁盘驱动器做一些假设。 让我们看看希捷的几个现代磁盘。 第一种称为 Cheetah 15K.5 [S09b],是一种高性能 SCSI 驱动器。 第二个是 Barracuda [S09a],是专为容量而设计的驱动器。 有关两者的详细信息,请参见图 37.5。 
Figure 37.5: Disk Drive Specs: SCSI Versus SATA
如您所见,驱动器具有完全不同的特性,并且在许多方面很好地总结了磁盘驱动器市场的两个重要组成部分。 第一个是“高性能”驱动器市场,驱动器被设计为尽可能快地旋转、提供低寻道时间和快速传输数据。 第二个是“容量”市场,其中每字节成本是最重要的方面; 因此,驱动器速度较慢,但将尽可能多的位打包到可用空间中。
根据这些数字,我们可以开始计算驱动器在上述两种工作负载下的表现。 让我们先看看随机工作负载。 假设每次 4 KB 读取发生在磁盘上的随机位置,我们可以计算每次这样的读取需要多长时间。 在 Cheetah 上:
平均寻道时间(4毫秒)仅取制造商报告的平均时间;请注意,完整的寻道(从面的一端到另一端)可能需要多花两到三倍的时间。平均旋转延迟直接从转速计算。15000转等于250 RPS(转每秒);因此,每次旋转需要4毫秒。平均而言,磁盘会旋转一半,因此平均时间为2毫秒。最后,传输时间就是传输的大小除以峰值速率;在这里,它非常小(30微秒;请注意,我们需要1000微秒才能得到1毫秒!)。
因此,从上面的方程,Cheetah 的大约等于6毫秒。为了计算I/O的速率,我们只需将传输的大小除以平均时间,就可以得到 Cheetah 在大约0.66 MB/s的随机工作负载下的
。用同样的方法计算 Barracuda 的
约为13.2 ms,慢了两倍多,因此速率约为0.31 MB/s。
现在让我们看看连续工作负载。在这里,我们可以假设在一个很长的传输之前有一次寻道和旋转延迟。为简单起见,假设传输的大小为100 MB。因此, Cheetah 和 Barracuda 的分别约为800 ms和950 ms。因此,I/O的速率非常接近峰值传输速率(分别为125 MB/s和105 MB/s)。图37.6总结了这些数字。

Figure 37.6: Disk Drive Performance: SCSI Versus SATA
该图表向我们展示了一些重要的东西。首先,也是最重要的一点,驱动性能在随机和连续工作负载之间存在巨大的差距,Cheetah 的差距几乎是200倍左右,Barracuda的差距超过300倍。这样我们就得到了计算机历史上最明显的设计技巧。
第二个更微妙的点:高端“性能”驱动器和低端“容量”驱动器之间的性能差异很大。 出于这个原因(和其他原因),人们通常愿意为前者支付高价,同时试图尽可能便宜地获得后者。
Aside:计算“平均”寻道(时间) 在许多书籍和论文中,你会看到平均寻道时间大约是整个寻道时间的三分之一。这从何而来? 事实证明,它来自一个基于平均寻道距离的简单计算,而不是时间。将磁盘想象成一组从0到n的磁道。因此,任意两个磁道x和y之间的寻道距离被计算为它们之间的差的绝对值:
%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-7C%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%22278%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%221073%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-79%22%20x%3D%222073%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-7C%22%20x%3D%222571%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=%5Cleft%7C%20x-y%5Cright%7C&id=cDMst)。 为了计算平均寻道距离,你需要做的就是首先将所有可能的寻道距离相加:
然后,除以不同可能的寻求数:
。为了计算和,我们只需使用积分形式:
为了计算内积分,我们把绝对值取出来:
解此式会得到
,可简化为
,现在我们要计算外积分:
得到:
记住,我们仍然需要除以总搜索次数(
)来计算平均搜索距离:
。因此,磁盘上的平均寻道距离,除以所有可能的寻道,是整个距离的三分之一。现在,当你听到一个平均寻道是一个完整寻道的三分之一时,你就知道它是从哪里来的了。
37.5 磁盘调度 Disk Scheduling
由于I/O的高成本,操作系统在决定向磁盘发出的I/O顺序方面一直扮演着重要角色。更具体地说,给定一组I/O请求,磁盘调度器(disk scheduler )检查请求并决定下一个调度[SCO90, JW91]。
与任务调度不同,每个任务的长度通常是未知的,通过磁盘调度,我们可以很好地猜测“任务”(即磁盘请求)需要多长时间。 通过估计请求的寻道和可能的旋转延迟,磁盘调度程序可以知道每个请求需要多长时间,因此(贪婪地)首先选择需要最少时间的请求。 因此,磁盘调度程序在其操作中将尝试遵循 SJF(shortest job first,最短任务优先)原则。
SSTF:最短寻道时间优先 SSTF: Shortest Seek Time First
一种早期的磁盘调度方法被称为最短寻道时间优先(shortest-seek-time-first,SSTF)(也称为shortest-seek-first或SSF)。SSTF根据磁道对I/O请求队列进行排序,在最近的磁道上选择请求首先完成。例如,假设磁头的当前位置在内部磁道上,我们有扇区21(中间磁道)和扇区2(外部磁道)的请求,然后我们会先向21发出请求,等待它完成,然后向2发出请求(图37.7)。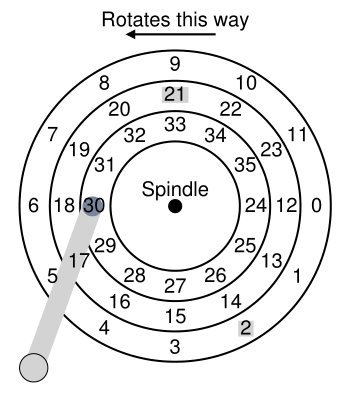
Figure 37.7: SSTF: Scheduling Requests 21 And 2
SSTF在这个例子中工作得很好,首先寻找到中间的轨道,然后是外部的轨道。然而,SSTF并不是万灵药,原因如下。首先,主机操作系统无法获得驱动器的几何形状;相反,它看到的是一个块数组。幸运的是,这个问题很容易解决。操作系统可以简单地实现最近块优先 (nearest-block-first,NBF),而不是 SSTF,它用最近的块地址调度请求。
第二个问题更为根本: 饿死(starvation)。想象一下,在上面的例子中,如果对内部磁道有一个稳定的请求流,也就是磁头当前的位置。对任何其他磁道的请求将被纯SSTF方法完全忽略。因此问题的关键在于:
关键的问题:怎样处理磁盘饿死 我们如何实现类似SSTF的调度,但避免饿死?
电梯(也叫SCAN或者C-SCAN) Elevator (a.k.a. SCAN or C-SCAN)
这个疑问的答案是在一段时间以前开发的(参见[CKR72]示例),并且相对简单。该算法最初称为SCAN,它只是在磁盘服务请求之间按顺序在磁道上来回移动。让我们把单次通过磁盘(从外磁道到内磁道,或从内磁道到外磁道)称为扫描。因此,如果请求已经在磁盘扫描中处理过的磁道上的块,它不会立即处理,而是排队直到下一次扫描(在另一个方向)。
SCAN有许多变体,它们都做相同的事情。例如,Coffman等人引入了F-SCAN,它在进行扫描时冻结待服务的队列[CKR72];此操作将在扫描期间进入的请求放置到一个队列中,以便稍后提供服务。这样做可以通过延迟对晚到的请求(但较近的请求)的服务来避免对远距离请求的饿死。
C-SCAN是另一种常见的变体,是Circular SCAN的缩写。该算法不是在磁盘的两个方向进行扫描,而是从外部到内部进行扫描,然后在外部磁道重新开始。这样做对内磁道和外磁道更公平一些,因为纯粹的来回SCAN更倾向于中间磁道,也就是说,在外磁道服务后,SCAN通过中间两次,然后再次回到外磁道。
出于现在应该清楚的原因,SCAN 算法(及其同类算法)有时被称为电梯算法,因为它的行为类似于电梯,它要么上升要么下降,而不仅仅是根据楼层的请求服务于楼层的请求。 更近。 想象一下,如果你从 10 楼下降到 1 楼,有人在 3 楼上电梯并按 4 楼,而电梯上升到 4 楼,因为它比 1 楼“更近”,那该有多烦人! 如您所见,电梯算法在现实生活中使用时,可以防止在电梯上发生冲突。 在磁盘中,它只是防止饿死。
不幸的是,SCAN和它的同类并不代表最好的调度技术。特别地,SCAN(甚至SSTF)实际上并没有尽可能地接近SJF的原理。特别是,它们忽略了旋转延迟。这就是另一个关键:
关键的问题:如何计入磁盘旋转延迟的消耗 我们如何通过同时考虑寻道和旋转延迟来实现更接近SJF的算法?
SPTF:最短定位时间优先 SPTF: Shortest Positioning Time First
在讨论我们问题的解决方案,最短定位时间优先(shortest positioning time first)或SPTF调度(有时也称为最短访问时间优先(shortest access time first)或SATF)之前,让我们先确认我们能更详细地了解问题。图37.8给出了一个示例。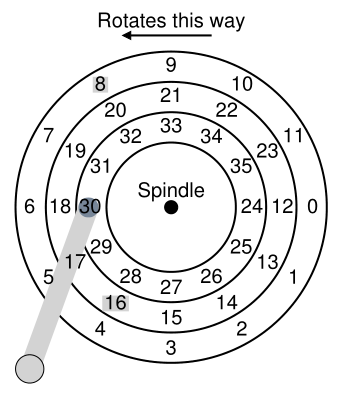
Figure 37.8: SSTF: Sometimes Not Good Enough
在这个例子中,磁头目前位于内轨道的30扇区上方。因此调度程序必须决定:它应该为下一个请求调度扇区16(在中间轨道上)还是扇区8(在外部轨道上)。那么它接下来应该服务哪个呢?
答案当然是“视情况而定”。 在工程中,结果几乎总是“视情况而定”,这反映了权衡是工程师生活的一部分; 这样的格言在紧要关头也很好,例如,当你不知道老板问题的答案时,你可能想试试这个宝石。 然而,我们最好知道它为什么要视情况而定,这就是我们在这里讨论的。
它所视情况而定的是寻道相比于旋转延迟的相对时间。如果,在我们的例子中,寻道时间比旋转延迟高得多,那么SSTF(和变体)就很好。然而,想象一下如果寻道比旋转延迟快一点。那么,在我们的示例中,在外部轨道上进一步查找服务请求8比在中间轨道上执行较短的查找以服务16更有意义,因为中间轨道在经过磁头之前必须一直旋转。
Tip:总是视情况而定(LIVNY定律) 正如我们的同事 Miron Livny 常说的那样,几乎任何问题都可以用“视情况而定”来回答。 但是,请谨慎使用,如果您以这种方式回答太多问题,人们将完全停止向您提问。 例如,有人问:“要不要去吃午饭?” 你回答:“看情况,你来吗?”
在现代驱动器上,正如我们上面所看到的,寻道和旋转延迟大致相同(当然取决于确切的请求),因此SPTF很有用,可以提高性能。然而,在操作系统中实现就更加困难了,因为操作系统通常不清楚磁道边界在哪里,或者磁头当前在哪里(从旋转的角度来说)。因此,SPTF通常是在驱动器内执行的,下面将进行说明。
其他调度问题 Other Scheduling Issues
在这篇关于基本磁盘操作、调度和相关主题的简要描述中,还有许多其他问题没有讨论。其中一个问题是:在现代系统中,磁盘调度在哪里执行?在较老的系统中,操作系统完成了所有的调度工作;在查看了一组挂起的请求后,操作系统将选择最好的一个,并将其发送到磁盘。当该请求完成时,将选择下一个请求,以此类推。那时磁盘比较简单,生活也是如此。
在现代系统中,磁盘可以容纳多个未完成的请求,并且本身具有复杂的内部调度程序(可以准确地实现 SPTF;在磁盘控制器内部,所有相关细节都可用,包括精确的磁头位置)。 因此,操作系统调度程序通常会选择它认为最好的少数请求(比如 16 个)并将它们全部发送到磁盘; 然后磁盘使用其磁头位置的内部信息和详细的磁道布局信息以最佳可能 (SPTF) 顺序为所述请求提供服务。
磁盘调度程序执行的另一个重要相关任务是I/O合并(I/O merging)。例如,想象一系列读取block 33、block 8、block 34的请求,如图37.8所示。在这种情况下,调度器应该将第33和34块的请求合并(merge)为一个单独的两个块请求; 调度程序所做的任何重新排序都是在合并的请求上执行的。合并在操作系统级别上尤其重要,因为它减少了发送到磁盘的请求数量,从而降低了开销。
现代调度器要解决的最后一个问题是: 在向磁盘发出I/O之前,系统应该等待多长时间?人们可能会天真地认为,一旦磁盘有了单个I/O,就应该立即向驱动器发出请求;这种方法称为连续工作(work-conserving),因为如果有服务请求,磁盘永远不会空闲。然而,对预期磁盘调度(anticipatory disk scheduling)的研究表明,有时稍等一会更好[ID01],这被称为非连续工作(non-work-conserving)方法。通过等待,新的“更好”的请求可能会到达磁盘,从而提高整体效率。 当然,决定何时等待以及等待多长时间可能很棘手。 有关详细信息,请参阅研究论文,或查看 Linux 内核实现以了解如何将这些想法转化为实践(如果您是雄心勃勃的那种)。
37.6 总结 Summary
我们已经对磁盘的工作方式进行了总结。总结实际上是一个详细的功能模型;它没有描述令人惊异的物理,电子,和材料科学,进入实际的驱动器设计。对于那些对这种性质的更多细节感兴趣的人,我们建议一个不同的专业(或者辅修);对于那些喜欢这个模型的人来说,很好!我们现在可以继续使用这个模型,在这些不可思议的设备上构建更有趣的系统。
References
[ADR03] “More Than an Interface: SCSI vs. ATA” by Dave Anderson, Jim Dykes, Erik Riedel. FAST ’03, 2003.
关于现代磁盘驱动器如何真正工作的最好的近期参考之一;对于任何有兴趣了解更多的人来说,这是必读的一本书。
[CKR72] “Analysis of Scanning Policies for Reducing Disk Seek Times” E.G. Coffman, L.A. Klimko, B. Ryan SIAM Journal of Computing, September 1972, Vol 1. No 3.
磁盘调度领域的一些早期工作。
[HK+17] “The Unwritten Contract of Solid State Drives” by Jun He, Sudarsun Kannan, Andrea C. Arpaci-Dusseau, Remzi H. Arpaci-Dusseau. EuroSys ’17, Belgrade, Serbia, April 2017.
我们采用了不成文合同的概念,并将其扩展到ssd。良好地使用ssd似乎和硬盘驱动器一样复杂,有时甚至更复杂。
[ID01] “Anticipatory Scheduling: A Disk-scheduling Framework To Overcome Deceptive Idleness In Synchronous I/O” by Sitaram Iyer, Peter Druschel. SOSP ’01, October 2001.
这是一篇很酷的论文,展示了等待如何改善磁盘调度:更好的请求可能就在他们的路上!
[JW91] “Disk Scheduling Algorithms Based On Rotational Position” by D. Jacobson, J. Wilkes. Technical Report HPL-CSP-91-7rev1, Hewlett-Packard, February 1991.
磁盘调度的一种更现代的方法。它仍然是一份技术报告(而不是一篇已发表的论文),因为作者被Seltzer等人抢先了[S90]。
[RW92] “An Introduction to Disk Drive Modeling” by C. Ruemmler, J. Wilkes. IEEE Computer, 27:3, March 1994.
对磁盘操作基础知识的极好介绍。有些东西已经过时了,但大多数基本的东西还在。
[SCO90] “Disk Scheduling Revisited” by Margo Seltzer, Peter Chen, John Ousterhout. USENIX 1990.
这篇论文讨论了旋转延迟在磁盘调度中的重要性。
[SG04] “MEMS-based storage devices and standard disk interfaces: A square peg in a round hole?” Steven W. Schlosser, Gregory R. Ganger FAST ’04, pp. 87-100, 2004 .
虽然本文的 MEMS 方面尚未产生影响,但对文件系统和磁盘之间契约的讨论非常精彩,而且是持久的贡献。 我们后来在这项工作的基础上研究了“固态硬盘的不成文合同”[HK+17]
[S09a] “Barracuda ES.2 data sheet” by Seagate, Inc.. https://www.seagate.com/docs/pdf/datasheet/disc/ds_barracuda_es.pdf
数据表; 阅读风险自负。 什么风险? 无聊。
[S09b] “Cheetah 15K.5” by Seagate, Inc.. http://www.seagate.com/docs/pdf/datasheet/disc/ds-cheetah-15k-5-us.pdf
参见上述数据表的注释。
Homework (Simulation)
本作业使用disk.py让您熟悉现代硬盘是如何工作的。它有许多不同的选项,并且与大多数其他模拟不同,它有一个图形动画来告诉你当磁盘在行动时到底发生了什么。有关详细信息,请参阅README。
- 计算以下请求集的寻道、旋转和传输时间:-a 0,-a 6,-a 30,-a 7,30,8,最后是-a 10,11,12,13。
- 执行上述相同的请求,但将寻道速率更改为不同的值:-S 2, -S 4, -S 8, -S 10, -S 40, -S 0.1。 时间如何变化?
- 执行上面相同的请求,但是改变旋转速率: -R 0.1, -R 0.5,-R 0.01。时代是如何变化的?
- FIFO并不总是最好的,例如,对于请求流 -a 7,30,8,应该以什么顺序处理请求?在此工作负载上运行最短寻道时间优先(SSTF)调度程序(-p SSTF);每一个请求需要多长时间(寻求、旋转、传输)才能被送达?
- 现在使用最短访问时间优先(SATF)调度程序(-p SATF)。这对-a 7,30,8 的工作负载有什么不同吗?找出一组SATF优于SSTF的请求;一般来说,SATF什么时候比SSTF好?
- 下面是尝试的请求流:-a 10,11,12,13。什么东西在运行时很糟糕?尝试添加磁道偏斜来解决这个问题(-o skew)。给定默认的寻道率,为了最大化性能,偏斜应该是多少?对于不同的寻道速率(例如,-S 2, -S 4)呢?一般来说,你能写出一个公式来算出偏斜吗?
- 指定每个区域具有不同密度的磁盘,例如 -z 10,20,30,它指定外部、中间和内部磁道上的块之间的角差。运行一些随机请求(例如,-a -1 -A 5,-1,0,它指定通过-a -1标志使用随机请求,并生成从0到最大的5个请求),并计算寻道、旋转和传输时间。使用不同的随机种子。外磁道、中磁道和内磁道的带宽(单位时间扇区)是多少?
- 调度窗口决定磁盘一次可以检查多少个请求。生成随机的工作负载(例如,-A 1000,-1,0,带有不同的种子),并查看当调度窗口从1更改到请求数量时,SATF调度程序需要多长时间。最大化性能需要多大的窗口?提示:使用-c标志,不要打开图形(-G)来快速运行这些。当调度窗口设置为1时,使用哪个策略有关系吗?
- 假设有SATF策略,创建一系列请求来饿死某个特定请求。给定该序列,如果使用有界(bounded)SATF (BSATF)调度方法,它将如何执行?在这种方法中,您指定调度窗口(例如,-w 4);只有当当前窗口中的所有请求都得到了服务时,调度器才会移动到下一个请求窗口。这能解决饿死问题吗?与SATF相比,它的表现如何?一般来说,磁盘应该如何在性能和避免饿死之间进行权衡?
- 到目前为止,我们看到的所有调度策略都是贪婪的;他们选择下一个最好的选择,而不是寻找最佳的调度。你能找到一组贪婪不是最佳的请求吗?

