在本节中,我们将研究**路由算法(routing algorithms)**,其目标是通过路由器网络确定从发送方到接收方的正确路径(相当于路由)。通常,“好的”路径是成本最低的路径。然而,我们将看到,在实践中,诸如策略问题(例如,诸如“属于组织Y的路由器x不应转发来自组织Z所拥有的网络的任何数据包”之类的规则)等现实世界的问题也会起作用。我们注意到,无论网络控制平面采用逐路由器控制方法还是逻辑集中式方法,数据包在从发送主机到接收主机的传输过程中必须始终有明确定义的路由器序列。因此,计算这些路径的路由算法至关重要,也是我们列出的十大基本重要网络概念的另一个候选者。<br />**图(graph)**是用来描述路由问题的。回想一下,图G=(N,E)是一组N个节点和一组边E,其中每条边都是来自N的一对节点。在网络层路由上下文中,图中的节点代表路由器(做出数据包转发决策的点),连接这些节点的边代表这些路由器之间的物理链路。计算机网络的这种图形抽象如图5.3所示。当我们研究BGP域间路由协议时,我们将看到节点代表网络,连接两个这样的节点的边代表两个网络之间的方向连接(direction connectivity,称为对等(peering))。要查看代表真实网络图的一些图表,请参见[CAIDA 2020];有关不同的基于图表的模型对互联网建模效果的讨论,请参见[Zegura 1997,Faloutsos 1999,Li 2004]。<br />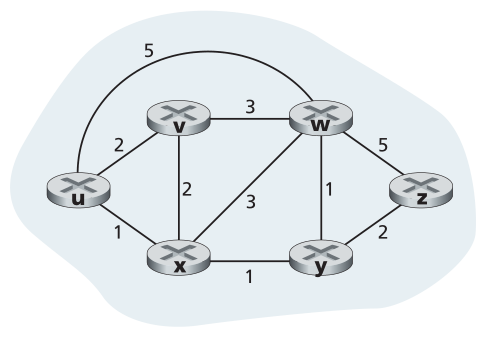<br />**Figure 5.3 ♦ Abstract graph model of a computer network**<br />**图5.3♦计算机网络的抽象图模型**<br />如图5.3所示,边也有一个表示其成本的值。通常,边缘的成本可能反映相应链路的物理长度(例如,跨洋链路可能比短途地面链路具有更高的成本)、链路速度或与链路相关的货币成本。出于我们的目的,我们将简单地将边成本视为给定的,而不会考虑它们是如何确定的。对于E中的任何边(x,y),我们用c(x,y)表示为结点x和y之间的边的代价。如果(x,y)对不属于E,我们设c(x,y)=∞。此外,在这里的讨论中,我们将只考虑无向图(即其边没有方向的图),因此边(x,y)与边(y,x)相同,并且c(x,y)=c(y,x);然而,我们将研究的算法可以很容易地扩展到每个方向具有不同成本的有向链路的情况。此外,如果(x,y)属于E,则称节点y是节点x的**邻居(neighbor)**。<br />假设成本被分配给图抽象中的各种边,路由算法的自然目标是确定源和目的地之间成本最低的路径。为了使这个问题更精确,回想一下,图G=(N,E)中的路径是节点(x1,x2,...,xp)的序列,使得每个对(x1,x2), (x2, x3),...,(xp-1,xp)都是E中的边。路径(x1,x2,...,xp)的成本只是路径上所有边成本的总和,即c(x1,x2) + c(x2,x3) + ... + c(xp-1,xp)。给定任意两个节点x和y,在这两个节点之间通常有许多路径,每条路径都有成本。这些路径中的一条或多条是**成本最低的路径(least-cost path)**。因此,**成本最低的问题是显而易见的:在源和目的地之间找到一条成本最低的路径**。例如,在图5.3中,源节点u和目的节点w之间的最低成本路径是(u,x,y,w),路径成本为3。请注意,如果图中的所有边都具有相同的成本,则最低成本路径也是**最短路径(shortest path)**(即,源节点和目标节点之间链路数量最少的路径)。<br />作为一个简单的练习,尝试查找图5.3中从节点u到z的最低成本路径,并思考一下您是如何计算该路径的。如果您和大多数人一样,您可以通过查看图5.3找到从u到z的路径,跟踪几条从u到z的路径,然后以某种方式说服自己,您选择的路径是所有可能路径中成本最低的。(您是否检查了u和z之间的所有17条可能路径?可能不会!)。这样的计算是**集中式路由算法(centralized routing algorithm)**的一个例子-路由算法在一个位置运行,即您的大脑,具有关于网络的完整信息。一般而言,我们可以根据路由算法是集中式的还是分散式的来对其进行分类。
- 集中式路由算法(centralized routing algorithm)使用有关网络的完整全局信息计算源和目的之间的最低开销路径。也就是说,该算法将所有节点之间的连通性和所有链路成本作为输入。这就要求算法在实际执行计算之前以某种方式获得该信息。计算本身可以在一个站点上运行(例如,如图5.2所示的逻辑集中控制器),或者可以在每个路由器的路由组件中复制(例如,如图5.1所示)。然而,这里的关键区别在于,该算法拥有关于连通性和链路成本的完整信息。具有全局状态信息的算法通常称为链路状态(link-state,LS)算法,因为该算法必须知道网络中每条链路的开销。我们将在第5.2.1节研究LS算法。
- 在分散式路由算法(decentralized routing algorithm)中,最小代价路径的计算由路由器以迭代、分布式的方式执行。没有任何节点具有关于所有网络链路的开销的完整信息。取而代之的是,每个节点开始时只知道它自己直连链路的开销。然后,通过与其相邻节点计算和交换信息的迭代过程,节点逐渐计算到目的地或目的地集合的最低成本路径。我们将在下面的第5.2.2节中研究的分散路由算法称为距离向量(distance-vector,DV)算法,因为每个节点都维护一个估计到网络中所有其他节点的成本(距离)的向量。这种在相邻路由器之间进行交互式消息交换的分散算法可能更自然地适用于路由器之间直接交互的控制平面,如图5.1所示。
对路由算法进行分类的第二种通用方法是根据它们是静态的还是动态的。在静态路由算法(static routing algorithms)中,路由随时间的变化非常缓慢,通常是人为干预的结果(例如,人工编辑链路开销)。动态路由算法(Dynamic routing algorithms)会随着网络流量负载或拓扑的变化而改变路由路径。动态算法可以定期运行,也可以直接响应拓扑或链路成本变化而运行。虽然动态算法对网络变化的响应更快,但它们也更容易受到路由环路和路由振荡等问题的影响。
对路由算法进行分类的第三种方法是根据它们是负载敏感还是负载不敏感。在负载敏感型算法(load-sensitive algorithm)中,链路开销会动态变化,以反映底层链路的当前拥塞程度。如果高开销与当前拥塞的链路相关联,则路由算法将倾向于选择此类拥塞链路周围的路由。虽然早期的ARPAnet路由算法对负载敏感[McQuillan 1980],但也遇到了许多困难[Huitema 1998]。当今的Internet路由算法(如RIP、OSPF和BGP)对负载不敏感,因为链路的开销不能明确反映其当前(或最近的)拥塞程度。
5.2.1 链路状态(LS)路由算法 The Link-State (LS) Routing Algorithm
回想一下,在链路状态算法中,网络拓扑和所有链路开销都是已知的,即可以作为LS算法的输入。实际上,这是通过让每个节点向网络中的所有其他节点广播链路状态数据包来实现的,每个链路状态数据包包含其连接的链路的标识和开销。实际上(例如,使用Internet的OSPF路由协议(在第5.3节中讨论)),这通常通过链路状态广播(link-state broadcast)算法来实现[Perlman 1999]。节点广播的结果是所有节点对网络有一个完全相同的视图。然后,每个节点都可以运行LS算法,并计算出与其他节点相同的最低成本路径集。
我们下面介绍的链路状态路由算法称为Dijkstra算法,以其发明者的名字命名。一个密切相关的算法是Prim算法;有关图算法的一般讨论,请参阅[Cormen 2001]。Dijkstra的算法计算从一个节点(源,我们将其称为u)到网络中所有其他节点的最低成本路径。Dijkstra的算法是迭代的,并且具有这样的性质:在算法的第k次迭代之后,k个目的节点知道成本最低的路径,并且在到所有目的节点的成本最低的路径中,这k条路径将具有k个最小的成本。让我们定义以下符号:
- D(v):在该算法迭代时从源节点到目的地v的最小成本路径的成本。
- P(v):沿着从源到v的当前最低成本路径的前一个节点(v的邻居)。
- N’:节点的子集;如果从源到v的最低成本路径是明确已知的,则v在N’中。
集中式路由算法由初始化步骤和循环组成。执行循环的次数等于网络中的节点数。在终止时,该算法将计算从源节点u到网络中的每一个其他节点的最短路径。
源节点u使用的链路状态(LS)算法 Link-State (LS) Algorithm for Source Node u

例如,让我们考虑图5.3中的网络,并计算从u到所有可能目的地的最低开销路径。表5.1中显示了算法计算的表格摘要,其中表中的每一行都给出了迭代结束时算法变量的值。让我们详细考虑几个第一步。
- 在初始化步骤中,将当前已知的从u到其直接连接的邻居v、x和w的最低成本路径分别初始化为2、1和5。特别要注意的是,由于这是从u到w的直接(一跳)链路的开销,所以到w的开销被设置为5(即使我们很快将看到确实存在较低开销的路径)。到y和z的开销被设置为无穷大,因为它们不直接连接到u。
- 在第一次迭代中,我们在那些尚未添加到集合N’中的节点中查找,并找到上一次迭代结束时成本最低的节点。该节点是x,成本为1,因此x被加到集合N’。然后执行LS算法的第12行以更新所有节点v的D(v),得到表5.1的第二行(步骤1)所示的结果。通向v的路径的成本不变。通过节点x到w(在初始化结束时为5)的路径的成本被发现具有成本4。因此,选择该较低成本的路径,并且沿从u开始的最短路径的w的前身被设置为x。类似地,到y(通过x)的成本被计算为2,并且相应地更新表。
- 在第二次迭代中,发现节点v和y具有最低成本路径(2),并且我们任意打破平局并将y添加到集合N’中,使得N’现在包含u、x和y。通过LS算法的第12行更新N’中还没有的其余节点(即节点v、w和z)的成本,从而产生表5.1中第三行所示的结果。
- 以此类推。。。

Table 5.1 ♦ Running the link-state algorithm on the network in Figure 5.3
表5.1♦在图5.3中的网络上运行链路状态算法
当LS算法终止时,对于每个节点,我们沿着从源节点开始的成本最低的路径拥有其前身。对于每个前身,我们也有它的前身,因此通过这种方式,我们可以构建从源到所有目的地的完整路径。然后,通过为每个目的地存储从u到目的地的最低开销路径上的下一跳节点,可以根据该信息构造节点(例如节点u)中的转发表。图5.4显示了图5.3中以 u 表示的网络最低成本路径和转发表。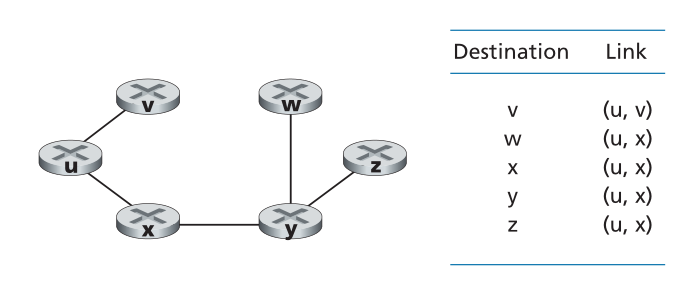
Figure 5.4 ♦ Least cost path and forwarding table for node u
图5.4节点 u 的最低成本路径和转发表
这个算法的计算复杂度是多少?也就是说,给定n个节点(不包括源),在最坏的情况下必须进行多少计算才能找到从源到所有目的地的成本最低的路径?在第一次迭代中,我们需要搜索所有n个节点,以确定具有最小成本的节点w,而且不是N’中的节点w。在第二次迭代中,我们需要检查n-1个节点以确定最小成本;在第三次迭代中,需要检查n-2个节点,依此类推。总体而言,我们需要在所有迭代中搜索的节点总数为n(n+1)/2,因此我们说LS算法的前面实现具有n平方的最坏情况复杂度:O(N2)。(该算法的一个更复杂的实现,使用一种称为堆的数据结构,可以在对数时间而不是线性时间内找到第9行的最小值,从而降低了复杂性。)
在结束对LS算法的讨论之前,让我们考虑一下可能出现的一种病理(pathology)。图5.5显示了一个简单的网络拓扑,其中链路成本等于链路上承载的负载,例如,它反映了可能会遇到的延迟。在本例中,链路成本不是对称的;也就是说,只有当链路(u,v)上的两个方向上承载的载荷相同时,c(u,v)才等于c(v,u)。在该示例中,节点z发起去往w的单位流量,节点x也发起去往w的单位流量,节点y注入也去往w的等于e的流量。初始路由如图5.5(A)所示,链路成本对应于承载的流量。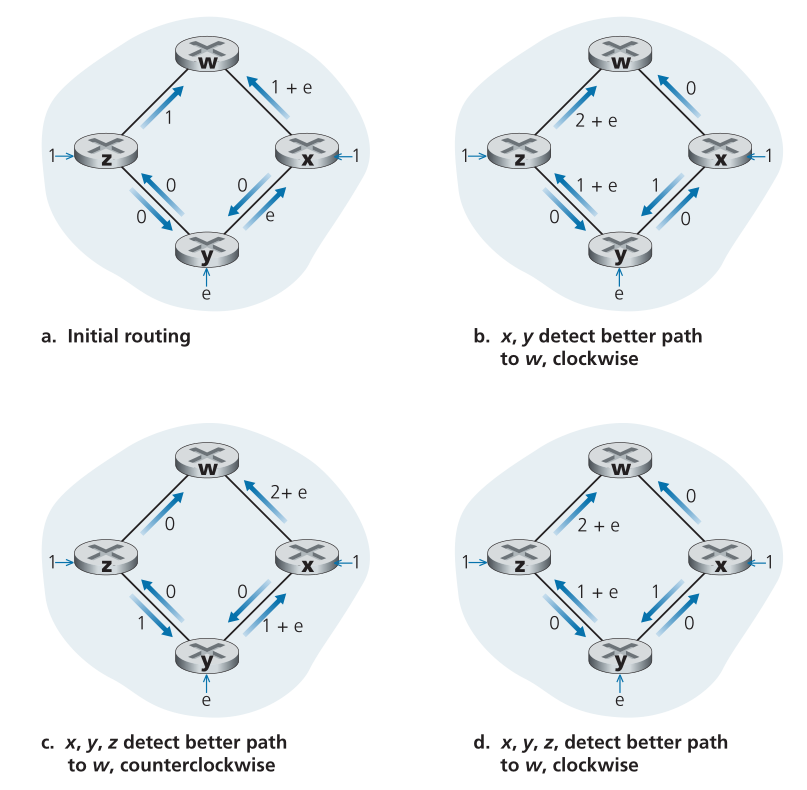
Figure 5.5 ♦ Oscillations with congestion-sensitive routing
图5.5♦拥塞敏感路由的振荡
当下一次运行LS算法时,节点y确定(基于图5.5(a)中所示的链路开销)到w的顺时针路径的开销为1,而到w的逆时针路径(它一直在使用)的开销为1+e。因此,y到w的最低开销路径现在是顺时针。类似地,x确定其到w的新的最低成本路径也是顺时针的,从而产生如图5.5(B)所示的成本。当下一次运行LS算法时,节点x、y和z都检测到逆时针方向到w的零成本路径,并且都将它们的流量路由到逆时针路由。下一次运行LS算法时,x、y和z都会将其流量路由到顺时针路由。
如何防止此类振荡(使用基于拥塞或延迟的链路度量的任何算法(而不仅仅是LS算法)都可能发生这种振荡)?一种解决方案是强制要求链路成本不取决于承载的流量-这是一种不可接受的解决方案,因为路由的一个目标是避免高度拥塞(例如,高延迟)的链路。另一种解决方案是确保并非所有路由器都同时运行LS算法。这似乎是一个更合理的解决方案,因为我们希望即使路由器以相同的周期运行LS算法,算法在每个节点的执行实例也不会相同。有趣的是,研究人员发现互联网中的路由器可以自我同步(Floyd Synchronization 1994)。也就是说,即使它们最初以相同的周期但在不同的时刻执行算法,算法执行实例最终可以在路由器处变得并保持同步。避免这种自同步的一种方法是让每台路由器将其发出链路通告的时间随机化。
学习了LS算法后,让我们考虑一下目前实际使用的另一种主要路由算法-距离矢量路由算法(distance-vector routing algorithm)。
5.2.2 距离矢量(DV)路由算法 The Distance-Vector (DV) Routing Algorithm
LS算法是使用全局信息的算法,而距离向量(DV)算法是迭代的、异步的和分布式的。它是分布式的,因为每个节点从其一个或多个直接连接的邻居接收一些信息,执行计算,然后将其计算结果分发回其邻居。它是迭代的,因为此过程会一直持续,直到邻居之间不再交换任何信息。(有趣的是,算法也是自动终止的-没有信号表明计算应该停止;它只是停止。)。该算法是异步的,因为它不需要所有节点彼此同步操作。我们将看到异步、迭代、自终止的分布式算法比集中式算法有趣得多!
在我们介绍DV算法之前,讨论存在于最低成本路径的成本之间的一个重要关系将是有益的。设dx(y)是从节点x到节点y的最低成本路径的成本。那么最低成本由著名的Bellman-Ford方程关联,即,
方程式中的取x的所有邻居。Bellman-Ford方程相当直观。实际上,从x到v之后,如果我们选择从v到y的最低成本路径,那么路径成本将是
。因为我们必须从某个邻居v开始遍历,所以从x到y的最小成本是所有邻居v的最小
。
但是,对于那些可能对等式的有效性持怀疑态度的人,让我们检查一下图5.3中的源节点u和目的节点z。源节点u有三个邻居:节点v、x和w。通过沿着图中的不同路径前进,很容易看到dv(z)=5、dx(z)=3和dw(z)=3。将这些值与成本c(u,v)=2、c(u,x)=1和c(u,w)=5一起代入公式5.1,得到du(z)=min{2+5, 5+3, 1+3}=4,这显然是正确的,这正是Dijskstra算法在相同的网络中给出的结果。这一快速验证应该有助于消除您可能存在的任何怀疑。
Bellman-Ford方程式不仅仅是一种求知欲。它实际上具有重要的实际意义:Bellman-Ford方程的解提供了节点x的转发表中的条目。要了解这一点,假设v是达到公式5.1中的最小值的任何相邻节点。然后,如果节点x想要沿着最低成本路径向节点y发送数据包,则它应该首先将数据包转发到节点v。因此,节点x的转发表将指定节点v*作为最终目的地y的下一跳路由器。Bellman-Ford方程的另一个重要的实际贡献是它建议了将在DV算法中发生的邻居到邻居通信的形式。
其基本思路如下。每个节点x以Dx(y)开始,Dx(y)是N中所有节点y的从其自身到节点x的最小成本路径的成本估计。让Dx=[Dx(y):y in N]是节点x的距离向量,其是从x到N中所有其他节点y的成本估计向量。利用DV算法,每个节点x维护以下路由信息:
- 对于每个邻居v,从x到直连邻居v的成本c(x,v)
- 节点x的距离向量,即Dx=[Dx(y):y in N],包含从x到N中所有其他节点y的成本估计
- 它的每个邻居的距离向量,即对于x的每个邻居v,Dv=[Dv(y):y in N]
在分布式异步算法中,每个节点不时地向每个邻居发送其距离矢量的副本。当节点x从其任何邻居w接收到新的距离向量时,它保存w的距离向量,然后使用Bellman-Ford方程来更新其自身的距离向量,如下所示:
如果节点x的距离向量作为该更新步骤的结果已经改变,则节点x将向其每个邻居发送其更新后的距离向量,这些邻居进而可以更新它们自己的距离向量。奇迹般地,只要所有节点继续以异步方式交换它们的距离向量,每个成本估计D**x(y)就会收敛到dx**(y),即从节点x到节点y的最小成本路径的实际成本[Bertsekas 1991]!
距离向量(DV)算法 Distance-Vector (DV) Algorithm
在每个节点上,x:
在DV算法中,当节点x看到其直接连接的链路之一中的成本变化或从某个邻居接收到距离向量更新时,它会更新其距离向量估计。但是,要更新给定目的地y的自身转发表,节点x真正需要知道的不是到y的最短路径距离,而是相邻节点v(y),即沿着到y的最短路径的下一跳路由器。正如您可能预期的那样,下一跳路由器v(y)是在DV算法的第14行中达到最小值的邻居v。(如果有多个邻居v达到最小值,则v(Y)可以是最小化邻居中的任何一个。)。因此,在第13-14行中,对于每个目的地y,节点x还确定v(y)并更新其目的地y的转发表。
回想一下,LS算法是一种集中式算法,它要求每个节点在运行Dijkstra算法之前首先获得完整的网络图。DV算法是分散的,不使用这样的全局信息。事实上,节点将拥有的唯一信息是到其直接连接的邻居的链路的成本以及从这些邻居接收的信息。每个节点等待来自任何邻居的更新(行10-11),在接收到更新时计算其新的距离向量(行14),并将其新的距离向量分发给其邻居(行16-17)。在实践中,许多路由协议都使用了类似DV的算法,包括Internet的RIP和BGP、ISO IDRP、Novell IPX以及最初的ARPAnet。
图5.6说明了图顶部所示的简单三节点网络的DV算法的工作原理。该算法的操作是以同步方式示出的,其中所有节点同时接收来自其邻居的距离向量,计算其新的距离向量,并通知其邻居其距离向量是否已改变。研究完此示例后,您应该确信算法也以异步方式正确运行,节点计算和更新生成/接收随时都会发生。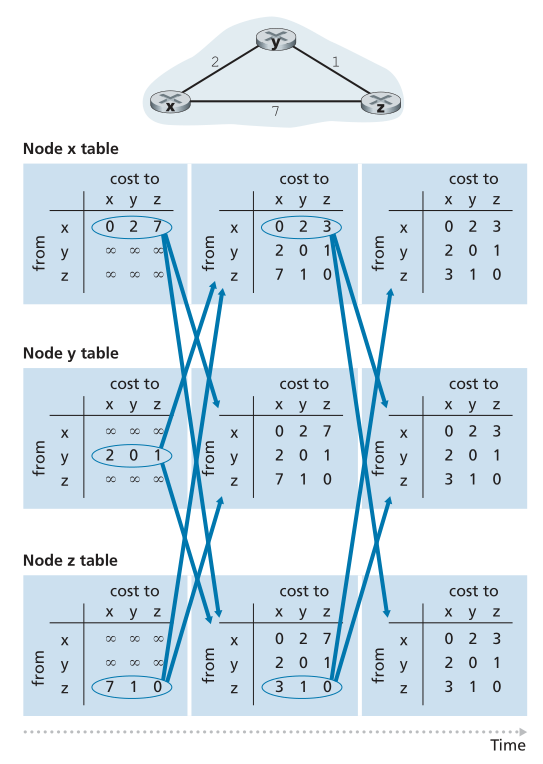
Figure 5.6 ♦ Distance-vector (DV) algorithm in operation
图5.6♦运行中的距离向量(DV)算法
图的最左边一列显示了三个节点中每个节点的三个初始路由表(initial routing tables)。例如,左上角的表是节点x的初始路由表。在特定的路由表中,每一行都是一个距离矢量-具体地说,每个节点的路由表都包括它自己的距离矢量及其每个邻居的距离矢量。因此,节点x的初始路由表中的第一行是Dx=[Dx(x),Dx(y),Dx(z)]=[0,2,7]。该表中的第二行和第三行分别是来自节点y和z的最近接收的距离矢量。因为在初始化节点x没有从节点y或z接收到任何东西,所以第二行和第三行中的条目被初始化为无穷大。
初始化后,每个节点将其距离向量发送到其两个邻居中的每一个。在图5.6中,从第一列表格到第二列表格的箭头说明了这一点。例如,节点x将其距离向量Dx=[0,2,7]发送给节点y和z。在接收到更新后,每个节点重新计算其自己的距离向量。例如,节点x计算
因此,第二列为每个节点显示该节点的新距离向量以及刚从其邻居接收到的距离向量。例如,请注意,节点x对节点z的最小成本Dx(z)的估计已从7变为3。还请注意,对于节点x,相邻节点y实现了DV算法第14行中的最小值;因此,在该算法的此阶段,我们在节点x具有v(y)=y和v(z)=y。
在节点重新计算其距离向量之后,它们会再次将更新后的距离向量发送给其邻居(如果发生了更改)。在图5.6中,从表的第二列到表的第三列的箭头说明了这一点。注意,只有节点x和z发送更新:节点y的距离向量没有改变,因此节点y不发送更新。收到更新后,节点然后重新计算其距离向量并更新其路由表,如第三列所示。
从邻居接收更新的距离矢量、重新计算路由表条目并将到目的地的最低成本路径的更改成本通知邻居的过程一直持续到没有发送更新消息为止。此时,由于没有发送更新消息,因此不会进行进一步的路由表计算,算法将进入静止状态;也就是说,所有节点都将在DV算法的第10-11行执行等待。该算法保持静止状态,直到链路成本改变,如下所述。
距离矢量算法:链路代价变化与链路故障 Distance-Vector Algorithm: Link-Cost Changes and Link Failure
当运行DV算法的节点检测到从其自身到邻居的链路开销的变化(第10-11行)时,它更新其距离向量(第13-14行),并且如果最低成本路径的成本发生变化,则将其新的距离向量通知其邻居(第16-17行)。图5.7(a)说明了从y到x的链路成本从4变为1的场景。这里我们只关注y和z到目的地x的距离表条目。DV算法会导致以下一系列事件发生:
- 在时间t0,y检测链路开销变化(开销已从4变为1),更新其距离矢量,并将此变化通知其邻居,因为其距离矢量已更改。
- 在时间t1,z从y接收更新并更新其表。它计算到x的新的最小开销(它已从开销5减少到开销2),并将其新的距离向量发送给其邻居。
- 在时间t2,y接收z的更新并更新其距离表。y的最小开销不变,因此y不会向z发送任何消息。算法进入静止状态。

Figure 5.7 ♦ Changes in link cost
图5.7♦链路成本的变化
因此,DV算法只需要两次迭代即可达到静止状态。关于x和y之间成本降低的好消息在网络上迅速传播。
现在让我们考虑一下当链路成本增加时会发生什么情况。假设x和y之间的链路成本从4增加到60,如图5.7(b)所示。
- 在链路成本变化之前,Dy(x)=4、Dy(z)=1、Dz(y)=1和Dz(x)=5。在时间t0,y检测链路成本变化(成本从4变为60)。y计算其到x的新的最小成本路径,其成本为
当然,从我们对网络的全局视角来看,我们可以看到,通过z计算的新成本是错误的。但是节点y拥有的唯一信息是它到x的直接成本是60,并且z最后一次告诉y z可以以5的成本到达x。因此,为了到达x,y现在将通过z进行路由,完全期望z能够以5的成本到达x。从t1开始,我们有一个路由循环(routing loop)-为了到达x,y路由通过z,z路由通过y。路由循环就像一个黑洞-在t1到达y或z的目的地为x的数据包将永远在这两个节点之间来回反弹(或者直到转发表发生变化)。
- 由于节点y已经计算了到x的新的最小成本,因此它在时间t1将其新的距离向量通知给z。
- 在t1之后的某个时间,z接收y的新的距离向量,这表明y到x的最小成本是6。z知道它可以以成本1到达y,因此计算出
的到x的新的最低成本。由于z到x的最小成本已经增加,因此它在t2将其新的距离向量通知y。
- 以类似的方式,在接收到z的新距离向量之后,y确定Dy(x)=8并向z发送其距离向量。然后,z确定Dz(x)=9,并向y发送其距离向量,依此类推。
这一过程将持续多久?您应该说服自己,循环将持续44次迭代(y和z之间的报文交换)-直到z最终计算出其通过y的路径开销大于50。在这时,z将(最终!)确定其到x的最低成本路径是通过其到x的直接连接。然后y将经由z路由到x。关于链路成本增加的坏消息的结果确实进展缓慢!如果链路开销c(y,x)从4更改为10,000,而开销c(z,x)为9999,会发生什么情况?由于这种情况,我们所看到的问题有时被称为计数到无穷大(count-to-infinity)的问题。
距离向量算法:添加毒性逆转 Distance-Vector Algorithm: Adding Poisoned Reverse
可以使用一种称为毒性逆转的技术来避免刚才描述的特定循环场景。这个想法很简单—如果z经过y到达目的地x,那么z将向y通告它到x的距离是无穷远的,也就是说,z将向y通告dz(x)=∞(即使z实际上知道dz(x)=5)。只要它通过y到达x,z就会继续向y撒这个善意的谎言。因为y认为z没有通往x的路径,所以y永远不会尝试通过z到达x,只要z继续经由y到达x(而且是关于这样做的谎言)。
现在让我们看看毒性逆转如何解决我们之前在图5.5(b)中遇到的特定循环问题。作为毒性逆转的结果,y的距离表显示Dz(x)=∞。当(x,y)链路的成本在时间t0从4变为60时,y更新其表并继续直接路由到x,尽管成本更高为60,并且将其新成本通知给x,即Dy(x)=60。在t1接收到更新后,z立即将其路由转换到x,以50为代价通过直接(z,x)链路。由于这是通向x的新的最低成本路径,并且由于该路径不再经过y,因此z现在通知y在t2处dz(x)=50。收到来自z的更新后,y使用Dy(x)=51更新其距离表。此外,由于z现在在y到x的最小开销路径上,y通过在时间t3通知z Dy(x)=∞(即使y知道Dy(x)实际上=51)来毒害从z到x的反向路径。
毒性逆转是否解决了一般的无穷大计数问题?事实并非如此。您应该说服自己,涉及三个或更多节点(而不仅仅是两个直接相邻的节点)的循环不会被毒性逆转技术检测到。
LS和DV路由算法的比较 A Comparison of LS and DV Routing Algorithms
DV和LS算法采用互补的方法来计算路由。在DV算法中,每个节点只与其直接相连的邻居通信,但它向邻居提供从它自己到网络中所有节点(它知道的)的最低成本估计。LS算法需要全局信息。因此,当在每台路由器中实施时(例如,如图4.2和5.1所示),每个节点都需要(通过广播)与所有其他节点通信,但它只告诉它们其直连链路的开销。让我们通过快速比较LS和DV算法的一些属性来结束我们对LS和DV算法的研究。回想一下,N是一组节点(路由器),E是一组边(链路)。
- 报文复杂性(Message complexity)。我们已经看到,LS要求每个节点知道网络中每条链路的开销。这需要发送O(|N||E|)条消息。此外,每当链路成本发生变化时,必须将新的链路成本发送到所有节点。DV算法需要在每次迭代中在直连邻居之间交换消息。我们已经看到,算法收敛所需的时间取决于许多因素。当链路开销改变时,只有当新的链路开销导致连接到该链路的节点之一的最低开销路径改变时,DV算法才会传播改变的链路开销的结果。
- 收敛速度(Speed of convergence)。我们已经看到,LS的实现是一个O(|N|2)算法,需要O(|N||E|)个消息。DV算法收敛速度慢,在收敛过程中可能会出现路由循环。DV还存在计数到无穷大的问题。
- 健壮性(Robustness)。如果路由器出现故障、行为不正常或遭到破坏,会发生什么情况?在LS下,路由器可能会为其连接的一条链路广播不正确的开销(但不能广播其他链路)。节点还可能损坏或丢弃作为LS广播一部分接收的任何数据包。但是LS节点只计算它自己的转发表;其他节点也为自己执行类似的计算。这意味着在LS下,路由计算在一定程度上是分开的,从而提供一定程度的健壮性。在DV下,节点可以向任何或所有目的地通告错误的最低成本路径。(事实上,1997年,一家小型ISP的故障路由器向国家主干路由器提供了错误的路由信息。这会导致其他路由器向出现故障的路由器发送大量流量,并导致互联网的大部分连接中断长达几个小时[Neumann 1997]。更一般地,我们注意到,在每次迭代中,节点在DV中的计算被传递给它的邻居,然后在下一次迭代中间接传递给它邻居的邻居。从这个意义上说,错误的节点计算可以在DV下在整个网络中传播。
归根结底,这两种算法都不是明显的赢家;事实上,这两种算法都在互联网上使用。

