回到 1.1 节，我们说过可以将 Internet 视为一种基础设施，它为在终端系统上运行的分布式应用程序提供服务。理想情况下，我们希望 Internet 服务能够在任意两个终端系统之间即时移动任意数量的数据，而不会丢失任何数据。唉，这是一个崇高的目标，在现实中是无法实现的。相反，**计算机网络必然会限制终端系统之间的吞吐量（每秒可以传输的数据量），在终端系统之间引入延迟，并且实际上可能会丢失数据包。**一方面，不幸的是，现实的物理定律引入了延迟和丢包并限制了吞吐量。另一方面，由于计算机网络存在这些问题，围绕如何处理这些问题存在许多引人入胜的问题——这些问题足以填满计算机网络课程并激发成千上万的博士论文！在本节中，我们将开始检查和量化计算机网络中的延迟、丢包和吞吐量。

1.4.1 数据包交换网络中延迟的概述 Overview of Delay in Packet-Switched Networks

回想一下，一个数据包从一台主机（源）开始，经过一系列路由器，并在另一台主机（目的地）中结束它的旅程。 当数据包沿着这条路径从一个节点（主机或路由器）传输到后续节点（主机或路由器）时，数据包在路径上的每个节点都会受到几种类型的延迟。 这些延迟中最重要的是节点处理延迟、排队延迟、传输延迟和传播延迟（nodal processing delay, queuing delay, transmission delay, and propagation delay）； 这些延迟累积在一起，形成总节点延迟（total nodal delay）。 许多 Internet 应用程序（例如搜索、Web 浏览、电子邮件、地图、即时消息和 IP 语音）的性能受到网络延迟的极大影响。 为了深入了解数据包交换和计算机网络，我们必须了解这些延迟的性质和重要性。

延迟的类型 Types of Delay

让我们在图 1.16 的内容中探索这些延迟。 作为源和目的地之间端到端路由的一部分，数据包从上游节点通过路由器 A 发送到路由器 B。我们的目标是描述路由器 A 的节点延迟。请注意，路由器 A 有一条通往路由器 B 的出站链路。该链路前面是一个队列（也称为缓冲区）。 当数据包从上游节点到达路由器 A 时，路由器 A 检查数据包的报头以确定数据包的适当出站链路，然后将数据包定向到此链路。在本例中，数据包的出站链路是通向路由器 B 的链路。只有当链路上当前没有其他数据包正在传输并且队列中没有其他数据包在它之前，才能在该链路上传输数据包； 如果链路当前繁忙，或者如果有其他数据包已经在排队等待该链路，则新到达的数据包将加入队列。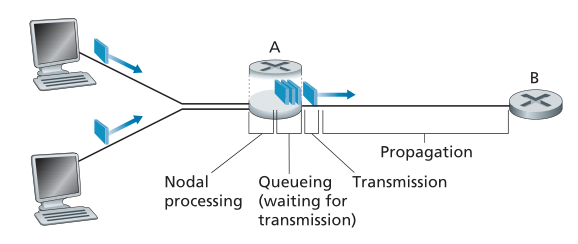

Figure 1.16 ♦ The nodal delay at router A

处理延迟 Processing Delay

检查数据包的报头并确定将数据包定向到何处所需的时间是处理延迟（processing delay）的一部分。 处理延迟还可能包括其他因素，例如检查在将数据包的位从上游节点传输到路由器 A 时发生的数据包中的位级错误所需的时间。高速路由器中的处理延迟通常在几微秒或更短的数量级。 在此节点处理之后，路由器将数据包定向到连接到路由器 B 的链路之前的队列。（在第 4 章中，我们将研究路由器如何操作的细节。）

排队延迟 Queuing Delay

在队列中，数据包在等待传输到链路上时会经历排队延迟（queuing delay）。 特定数据包的排队延迟长度将取决于排队等待传输到链路上的较早到达数据包的数量。 如果队列为空并且当前没有其他数据包正在传输，那么我们数据包的排队延迟将为零。 另一方面，如果流量很大并且还有许多其他数据包在等待传输，则排队延迟会很长。我们将很快看到，一个到达的数据包可能期望找到的数据包的数量是到达队列的流量的强度和性质的函数。实际上，排队延迟可以是微秒到毫秒的数量级。

传输延迟 Transmission Delay

假设数据包以先到先服务（first-come-first-served）的方式传输，这在数据包交换网络中很常见，我们的数据包只能在传输完之前到达的所有数据包之后才能被传输。 用L比特表示数据包的长度，用R比特/秒表示路由器A到路由器B的链路传输速率。 例如，对于 10 Mbps 以太网链路，速率为 R = 10 Mbps； 对于 100 Mbps 以太网链路，速率为 R = 100 Mbps。 传输延迟（transmission delay）为 L/R。 这是将数据包的所有位推送（即传输）到链路中所需的时间。 实际上，传输延迟通常在微秒到毫秒的数量级。

传播延迟 Propagation Delay

一旦一个比特被推入链路，它需要传播到路由器 B。从链路开始传播到路由器 B 所需的时间就是传播延迟。 比特以链路的传播速度传播。 传播速度取决于链路的物理介质（即光纤、双绞铜线等）并且在此范围内：

这等于或略小于光速。 传播延迟是两个路由器之间的距离除以传播速度。 即传播延迟为d/s，其中d是路由器A和路由器B之间的距离，s是链路的传播速度。 一旦数据包的最后一位传播到节点 B，它和数据包的所有前面的位都存储在路由器 B 中。然后整个过程继续由路由器 B 现在执行转发。 在广域网中，传播延迟为毫秒级。

比较传输和传播延迟 Comparing Transmission and Propagation Delay

计算机网络领域的新手有时很难理解传输延迟和传播延迟之间的区别。 这种差异很微妙，但很重要。 传输延迟是路由器推出（push out）数据包所需的时间； 它是数据包长度和链路传输速率的函数，与两台路由器之间的距离无关。 另一方面，传播延迟是从一个路由器传播到下一个路由器所需的时间。 它是两个路由器之间距离的函数，但与数据包的长度或链路的传输速率无关。
一个类比可能会澄清传输和传播延迟的概念。考虑一条每 100 公里有一个收费站的高速公路，如图 1.17 所示。 您可以将收费站之间的高速公路段视为链路，将收费站视为路由器。 假设汽车以 100 公里/小时的速度在高速公路上行驶（即传播）（即，当汽车离开收费站时，它会立即加速到 100 公里/小时，并在收费站之间保持该速度）。 假设接下来有 10 辆汽车作为一个车队一起行驶，以固定的顺序彼此跟随。您可以将每辆车想象成一个比特（bit），将车队想象成一个数据包（packet）。还假设每个收费站以每 12 秒一辆车的速度服务（即传输）一辆汽车，并且现在是深夜，因此车队的汽车是高速公路上唯一的汽车。最后，假设当车队的第一辆车到达收费站时，它会在入口处等待，直到其他九辆车到达并在其后面排队。 （因此，整个车队必须存放在收费站才能开始转发。）收费站将整个车队推上高速公路所需的时间为（10辆汽车）/（5辆汽车/分钟）= 2分钟。这个时间类似于路由器中的传输延迟。汽车从一个收费站出口到下一个收费站所需的时间为100公里/（100公里/小时）=1小时。这个时间类似于传播延迟。因此，从车队停在收费站前到车队停在下一个收费站前的时间是传输延迟和传播延迟的总和——在本例中为 62 分钟。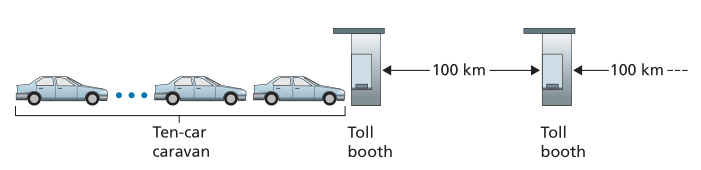

Figure 1.17 ♦ Caravan analogy
让我们进一步探讨这个类比。 如果车队的收费站服务时间大于汽车在收费站之间行驶的时间，会发生什么？ 例如，现在假设汽车以 1,000 公里/小时的速度行驶，收费站以每分钟一辆车的速度服务汽车。 那么两个收费站之间的行车延迟是 6 分钟，服务车队的时间是 10 分钟。 在这种情况下，车队中的前几辆汽车将在车队中的最后几辆汽车离开第一个收费站之前到达第二个收费站。 这种情况也出现在数据包交换网络中——数据包中的第一个比特可以到达路由器，而数据包中的许多剩余比特仍在等待由前一个路由器传输。
如果一张图片说一千个字，那么一部动画必须说一百万个字。 这本教科书的网站提供了一个交互式动画，可以很好地说明和对比传输延迟和传播延迟。 强烈鼓励读者访问该动画。 [Smith 2009] 还提供了关于传播、排队和传输延迟的非常易读的讨论。
如果让 dproc、dqueue、dtrans 和 dprop 表示处理、排队、传输和传播延迟，则总节点延迟由下式给出：

这些延迟分量的贡献可能会有很大差异。 例如，对于连接同一大学校园内的两个路由器的链路，dprop 可以忽略不计（例如，几微秒）； 然而，对于通过地球静止卫星链路互连的两个路由器，dprop 是数百毫秒，并且可以是 dnodal 中的主要项。同样，dtrans 的范围可以从可忽略不计到显著。 对于 10 Mbps 或更高的传输速率（例如，对于 LAN），它的贡献通常可以忽略不计； 但是，对于通过低速拨号调制解调器（low-speed dial-up modem）链接发送的大型 Internet 数据包，它可能需要数百毫秒。 处理延迟 d**proc** 通常可以忽略不计； 但是，它强烈影响路由器的最大吞吐量，即路由器可以转发数据包的最大速率。

1.4.2 排队延迟和丢包 Queuing Delay and Packet Loss

节点延迟中最复杂和最有趣的部分是排队延迟，dqueue。事实上，排队延迟在计算机网络中是如此重要和有趣，以至于已经有数以千计的论文和大量的书籍与它相关 [Bertsekas 1991;Kleinrock 1975，Kleinrock 1976]。我们这里只对排队延迟进行高层次、直观的讨论；好奇的读者可能想要浏览一些书籍（甚至最终写一篇关于该主题的博士论文！）。与其他三种延迟（即 dproc、dtrans 和 dprop）不同，排队延迟可能因数据包而异。例如，如果有 10 个数据包同时到达一个空队列，则第一个发送的数据包不会遭受排队延迟，而最后发送的数据包将遭受相对较大的排队延迟（同时等待其他 9 个数据包的发送） ）。因此，在表征排队延迟时，通常使用统计度量，例如平均排队延迟、排队延迟方差、排队延迟超过某个指定值的概率。
什么时候排队延迟大，什么时候小？ 这个问题的答案取决于流量到达队列的速率、链路的传输速率以及到达流量的性质，即流量是周期性到达还是突发到达。 为了深入了解这里，让 a 表示数据包到达队列的平均速率（a 以数据包/秒为单位）。 回想一下，R 是传输速率； 也就是说，它是比特被推出队列的速率（以比特/秒为单位）。 还假设，为简单起见，所有数据包都由 L 位组成。 那么比特到达队列的平均速率是 La 比特/秒。 最后，假设队列非常大，因此它基本上可以容纳无限数量的位。比率 La/R，称为流量强度（traffic intensity），通常在估计排队延迟的程度方面起着重要作用。 如果 La/R > 1，则比特到达队列的平均速率超过比特可以从队列中传输的速率。 在这种不幸的情况下，队列将趋于无限制地增加，排队延迟将接近无穷大！ 因此，流量工程的黄金法则之一是：设计您的系统，使流量强度不大于 1。
现在考虑 La/R ≤ 1 的情况。这里，到达业务的性质会影响排队延迟。 例如，如果数据包周期性地到达——即每 L/R 秒一个数据包到达——那么每个数据包都会到达一个空队列，并且不会有排队延迟。 另一方面，如果数据包以突发方式但周期性地到达，则可能存在显著的平均排队延迟。 例如，假设 N 个数据包每 (L/R)N 秒同时到达。 那么第一个传输的数据包没有排队延迟； 发送的第二个数据包有L/R秒的排队延迟； 更一般地，传输的第 n 个数据包的排队延迟为 (n - 1) L/R 秒。 我们将其留作练习，让您计算本例中的平均排队延迟。
上面描述的两个周期性到达的例子有点学术性。通常，队列的到达过程是随机的；也就是说，到达不遵循任何模式，并且数据包以随机的时间间隔开。在这种更现实的情况下，数量 La/R 通常不足以完全表征排队延迟统计数据。尽管如此，它有助于直观地了解排队延迟的程度。特别是，如果流量强度接近于零，则到达的数据包很少而且相距很远，并且到达的数据包不太可能在队列中找到另一个数据包。因此，平均排队延迟将接近于零。另一方面，当流量强度接近1时，会出现到达率超过传输容量的时间间隔（由于数据包到达率的变化），在这些时间段内会形成队列；当到达率小于传输容量时，队列长度会缩小。尽管如此，随着流量强度接近1，平均队列长度变得越来越大。平均排队延迟对流量强度的定性依赖如图 1.18 所示。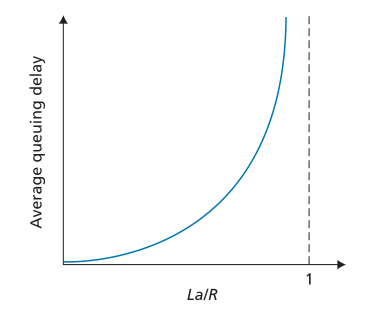

Figure 1.18 ♦ Dependence of average queuing delay on traffic intensity
图 1.18 的一个重要方面是当交通强度接近 1 时，平均排队延迟迅速增加。 强度的小百分比增加将导致延迟的更大百分比增加。 或许你在高速公路上遇到过这种现象。 如果您经常在通常拥堵的道路上行驶，那么该道路通常拥堵的事实意味着其交通强度接近 1。如果某些事件导致的流量甚至比平时略大，则您遇到的延迟可能会很大。
要真正了解排队延迟的含义，我们再次鼓励您访问教科书网站，该网站为排队提供了交互式动画。 如果您将数据包到达率设置得足够高，使流量强度超过 1，您将看到队列随着时间的推移慢慢增加。
在我们上面的讨论中，我们假设队列能够容纳无限数量的数据包。 实际上，链路前面的队列具有有限的容量，尽管排队容量（queuing capacity）在很大程度上取决于路由器的设计和成本。 由于队列容量是有限的，当流量强度接近 1 时，数据包延迟并不会真正接近无穷大。相反，一个数据包到达时可以发现一个已满的队列。 由于没有地方存储这样的数据包，路由器将丢弃（drop）该数据包； 也就是说，数据包将丢失（lost）。 当交通强度大于 1 时，可以在交互动画中再次看到队列中的这种溢出。
从终端系统的角度来看，数据包丢失看起来就像一个数据包已传输到网络核心，但从未在目的地网络中出现。 丢失数据包的比例随着流量强度的增加而增加。因此，节点的性能通常不仅根据延迟来衡量，而且还根据数据包丢失的概率来衡量。 正如我们将在后续章节中讨论的那样，丢失的数据包可能会在端到端的基础上重新传输，以确保所有数据最终都从源传输到目的地。

1.4.3 端到端延迟 End-to-End Delay

到目前为止，我们的讨论集中在节点延迟上，即单个路由器的延迟。 现在让我们考虑从源到目的地的总延迟。 为了理解这个概念，假设源主机和目标主机之间有 N-1 个路由器。 我们暂时还假设网络不拥塞（因此排队延迟可以忽略不计），每个路由器和源主机的处理延迟为 dproc，每个路由器和源主机的传输速率为 R 位 /sec，每个链路上的传播延迟是dprop。 节点延迟累积并给出端到端延迟，
%20%5Ctag%7B1.2%7D%3C%2Ftitle%3E%0A%3Cdefs%20aria-hidden%3D%22true%22%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-28%22%20d%3D%22M94%20250Q94%20319%20104%20381T127%20488T164%20576T202%20643T244%20695T277%20729T302%20750H315H319Q333%20750%20333%20741Q333%20738%20316%20720T275%20667T226%20581T184%20443T167%20250T184%2058T225%20-81T274%20-167T316%20-220T333%20-241Q333%20-250%20318%20-250H315H302L274%20-226Q180%20-141%20137%20-14T94%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-31%22%20d%3D%22M213%20578L200%20573Q186%20568%20160%20563T102%20556H83V602H102Q149%20604%20189%20617T245%20641T273%20663Q275%20666%20285%20666Q294%20666%20302%20660V361L303%2061Q310%2054%20315%2052T339%2048T401%2046H427V0H416Q395%203%20257%203Q121%203%20100%200H88V46H114Q136%2046%20152%2046T177%2047T193%2050T201%2052T207%2057T213%2061V578Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2E%22%20d%3D%22M78%2060Q78%2084%2095%20102T138%20120Q162%20120%20180%20104T199%2061Q199%2036%20182%2018T139%200T96%2017T78%2060Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-32%22%20d%3D%22M109%20429Q82%20429%2066%20447T50%20491Q50%20562%20103%20614T235%20666Q326%20666%20387%20610T449%20465Q449%20422%20429%20383T381%20315T301%20241Q265%20210%20201%20149L142%2093L218%2092Q375%2092%20385%2097Q392%2099%20409%20186V189H449V186Q448%20183%20436%2095T421%203V0H50V19V31Q50%2038%2056%2046T86%2081Q115%20113%20136%20137Q145%20147%20170%20174T204%20211T233%20244T261%20278T284%20308T305%20340T320%20369T333%20401T340%20431T343%20464Q343%20527%20309%20573T212%20619Q179%20619%20154%20602T119%20569T109%20550Q109%20549%20114%20549Q132%20549%20151%20535T170%20489Q170%20464%20154%20447T109%20429Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-29%22%20d%3D%22M60%20749L64%20750Q69%20750%2074%20750H86L114%20726Q208%20641%20251%20514T294%20250Q294%20182%20284%20119T261%2012T224%20-76T186%20-143T145%20-194T113%20-227T90%20-246Q87%20-249%2086%20-250H74Q66%20-250%2063%20-250T58%20-247T55%20-238Q56%20-237%2066%20-225Q221%20-64%20221%20250T66%20725Q56%20737%2055%20738Q55%20746%2060%20749Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-64%22%20d%3D%22M366%20683Q367%20683%20438%20688T511%20694Q523%20694%20523%20686Q523%20679%20450%20384T375%2083T374%2068Q374%2026%20402%2026Q411%2027%20422%2035Q443%2055%20463%20131Q469%20151%20473%20152Q475%20153%20483%20153H487H491Q506%20153%20506%20145Q506%20140%20503%20129Q490%2079%20473%2048T445%208T417%20-8Q409%20-10%20393%20-10Q359%20-10%20336%205T306%2036L300%2051Q299%2052%20296%2050Q294%2048%20292%2046Q233%20-10%20172%20-10Q117%20-10%2075%2030T33%20157Q33%20205%2053%20255T101%20341Q148%20398%20195%20420T280%20442Q336%20442%20364%20400Q369%20394%20369%20396Q370%20400%20396%20505T424%20616Q424%20629%20417%20632T378%20637H357Q351%20643%20351%20645T353%20664Q358%20683%20366%20683ZM352%20326Q329%20405%20277%20405Q242%20405%20210%20374T160%20293Q131%20214%20119%20129Q119%20126%20119%20118T118%20106Q118%2061%20136%2044T179%2026Q233%2026%20290%2098L298%20109L352%20326Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-65%22%20d%3D%22M39%20168Q39%20225%2058%20272T107%20350T174%20402T244%20433T307%20442H310Q355%20442%20388%20420T421%20355Q421%20265%20310%20237Q261%20224%20176%20223Q139%20223%20138%20221Q138%20219%20132%20186T125%20128Q125%2081%20146%2054T209%2026T302%2045T394%20111Q403%20121%20406%20121Q410%20121%20419%20112T429%2098T420%2082T390%2055T344%2024T281%20-1T205%20-11Q126%20-11%2083%2042T39%20168ZM373%20353Q367%20405%20305%20405Q272%20405%20244%20391T199%20357T170%20316T154%20280T149%20261Q149%20260%20169%20260Q282%20260%20327%20284T373%20353Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-6E%22%20d%3D%22M21%20287Q22%20293%2024%20303T36%20341T56%20388T89%20425T135%20442Q171%20442%20195%20424T225%20390T231%20369Q231%20367%20232%20367L243%20378Q304%20442%20382%20442Q436%20442%20469%20415T503%20336T465%20179T427%2052Q427%2026%20444%2026Q450%2026%20453%2027Q482%2032%20505%2065T540%20145Q542%20153%20560%20153Q580%20153%20580%20145Q580%20144%20576%20130Q568%20101%20554%2073T508%2017T439%20-10Q392%20-10%20371%2017T350%2073Q350%2092%20386%20193T423%20345Q423%20404%20379%20404H374Q288%20404%20229%20303L222%20291L189%20157Q156%2026%20151%2016Q138%20-11%20108%20-11Q95%20-11%2087%20-5T76%207T74%2017Q74%2030%20112%20180T152%20343Q153%20348%20153%20366Q153%20405%20129%20405Q91%20405%2066%20305Q60%20285%2060%20284Q58%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2212%22%20d%3D%22M84%20237T84%20250T98%20270H679Q694%20262%20694%20250T679%20230H98Q84%20237%2084%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-3D%22%20d%3D%22M56%20347Q56%20360%2070%20367H707Q722%20359%20722%20347Q722%20336%20708%20328L390%20327H72Q56%20332%2056%20347ZM56%20153Q56%20168%2072%20173H708Q722%20163%20722%20153Q722%20140%20707%20133H70Q56%20140%2056%20153Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-4E%22%20d%3D%22M234%20637Q231%20637%20226%20637Q201%20637%20196%20638T191%20649Q191%20676%20202%20682Q204%20683%20299%20683Q376%20683%20387%20683T401%20677Q612%20181%20616%20168L670%20381Q723%20592%20723%20606Q723%20633%20659%20637Q635%20637%20635%20648Q635%20650%20637%20660Q641%20676%20643%20679T653%20683Q656%20683%20684%20682T767%20680Q817%20680%20843%20681T873%20682Q888%20682%20888%20672Q888%20650%20880%20642Q878%20637%20858%20637Q787%20633%20769%20597L620%207Q618%200%20599%200Q585%200%20582%202Q579%205%20453%20305L326%20604L261%20344Q196%2088%20196%2079Q201%2046%20268%2046H278Q284%2041%20284%2038T282%2019Q278%206%20272%200H259Q228%202%20151%202Q123%202%20100%202T63%202T46%201Q31%201%2031%2010Q31%2014%2034%2026T39%2040Q41%2046%2062%2046Q130%2049%20150%2085Q154%2091%20221%20362L289%20634Q287%20635%20234%20637Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-70%22%20d%3D%22M23%20287Q24%20290%2025%20295T30%20317T40%20348T55%20381T75%20411T101%20433T134%20442Q209%20442%20230%20378L240%20387Q302%20442%20358%20442Q423%20442%20460%20395T497%20281Q497%20173%20421%2082T249%20-10Q227%20-10%20210%20-4Q199%201%20187%2011T168%2028L161%2036Q160%2035%20139%20-51T118%20-138Q118%20-144%20126%20-145T163%20-148H188Q194%20-155%20194%20-157T191%20-175Q188%20-187%20185%20-190T172%20-194Q170%20-194%20161%20-194T127%20-193T65%20-192Q-5%20-192%20-24%20-194H-32Q-39%20-187%20-39%20-183Q-37%20-156%20-26%20-148H-6Q28%20-147%2033%20-136Q36%20-130%2094%20103T155%20350Q156%20355%20156%20364Q156%20405%20131%20405Q109%20405%2094%20377T71%20316T59%20280Q57%20278%2043%20278H29Q23%20284%2023%20287ZM178%20102Q200%2026%20252%2026Q282%2026%20310%2049T356%20107Q374%20141%20392%20215T411%20325V331Q411%20405%20350%20405Q339%20405%20328%20402T306%20393T286%20380T269%20365T254%20350T243%20336T235%20326L232%20322Q232%20321%20229%20308T218%20264T204%20212Q178%20106%20178%20102Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-72%22%20d%3D%22M21%20287Q22%20290%2023%20295T28%20317T38%20348T53%20381T73%20411T99%20433T132%20442Q161%20442%20183%20430T214%20408T225%20388Q227%20382%20228%20382T236%20389Q284%20441%20347%20441H350Q398%20441%20422%20400Q430%20381%20430%20363Q430%20333%20417%20315T391%20292T366%20288Q346%20288%20334%20299T322%20328Q322%20376%20378%20392Q356%20405%20342%20405Q286%20405%20239%20331Q229%20315%20224%20298T190%20165Q156%2025%20151%2016Q138%20-11%20108%20-11Q95%20-11%2087%20-5T76%207T74%2017Q74%2030%20114%20189T154%20366Q154%20405%20128%20405Q107%20405%2092%20377T68%20316T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-6F%22%20d%3D%22M201%20-11Q126%20-11%2080%2038T34%20156Q34%20221%2064%20279T146%20380Q222%20441%20301%20441Q333%20441%20341%20440Q354%20437%20367%20433T402%20417T438%20387T464%20338T476%20268Q476%20161%20390%2075T201%20-11ZM121%20120Q121%2070%20147%2048T206%2026Q250%2026%20289%2058T351%20142Q360%20163%20374%20216T388%20308Q388%20352%20370%20375Q346%20405%20306%20405Q243%20405%20195%20347Q158%20303%20140%20230T121%20120Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-63%22%20d%3D%22M34%20159Q34%20268%20120%20355T306%20442Q362%20442%20394%20418T427%20355Q427%20326%20408%20306T360%20285Q341%20285%20330%20295T319%20325T330%20359T352%20380T366%20386H367Q367%20388%20361%20392T340%20400T306%20404Q276%20404%20249%20390Q228%20381%20206%20359Q162%20315%20142%20235T121%20119Q121%2073%20147%2050Q169%2026%20205%2026H209Q321%2026%20394%20111Q403%20121%20406%20121Q410%20121%20419%20112T429%2098T420%2083T391%2055T346%2025T282%200T202%20-11Q127%20-11%2081%2037T34%20159Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2B%22%20d%3D%22M56%20237T56%20250T70%20270H369V420L370%20570Q380%20583%20389%20583Q402%20583%20409%20568V270H707Q722%20262%20722%20250T707%20230H409V-68Q401%20-82%20391%20-82H389H387Q375%20-82%20369%20-68V230H70Q56%20237%2056%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-74%22%20d%3D%22M26%20385Q19%20392%2019%20395Q19%20399%2022%20411T27%20425Q29%20430%2036%20430T87%20431H140L159%20511Q162%20522%20166%20540T173%20566T179%20586T187%20603T197%20615T211%20624T229%20626Q247%20625%20254%20615T261%20596Q261%20589%20252%20549T232%20470L222%20433Q222%20431%20272%20431H323Q330%20424%20330%20420Q330%20398%20317%20385H210L174%20240Q135%2080%20135%2068Q135%2026%20162%2026Q197%2026%20230%2060T283%20144Q285%20150%20288%20151T303%20153H307Q322%20153%20322%20145Q322%20142%20319%20133Q314%20117%20301%2095T267%2048T216%206T155%20-11Q125%20-11%2098%204T59%2056Q57%2064%2057%2083V101L92%20241Q127%20382%20128%20383Q128%20385%2077%20385H26Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-61%22%20d%3D%22M33%20157Q33%20258%20109%20349T280%20441Q331%20441%20370%20392Q386%20422%20416%20422Q429%20422%20439%20414T449%20394Q449%20381%20412%20234T374%2068Q374%2043%20381%2035T402%2026Q411%2027%20422%2035Q443%2055%20463%20131Q469%20151%20473%20152Q475%20153%20483%20153H487Q506%20153%20506%20144Q506%20138%20501%20117T481%2063T449%2013Q436%200%20417%20-8Q409%20-10%20393%20-10Q359%20-10%20336%205T306%2036L300%2051Q299%2052%20296%2050Q294%2048%20292%2046Q233%20-10%20172%20-10Q117%20-10%2075%2030T33%20157ZM351%20328Q351%20334%20346%20350T323%20385T277%20405Q242%20405%20210%20374T160%20293Q131%20214%20119%20129Q119%20126%20119%20118T118%20106Q118%2061%20136%2044T179%2026Q217%2026%20254%2059T298%20110Q300%20114%20325%20217T351%20328Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-73%22%20d%3D%22M131%20289Q131%20321%20147%20354T203%20415T300%20442Q362%20442%20390%20415T419%20355Q419%20323%20402%20308T364%20292Q351%20292%20340%20300T328%20326Q328%20342%20337%20354T354%20372T367%20378Q368%20378%20368%20379Q368%20382%20361%20388T336%20399T297%20405Q249%20405%20227%20379T204%20326Q204%20301%20223%20291T278%20274T330%20259Q396%20230%20396%20163Q396%20135%20385%20107T352%2051T289%207T195%20-10Q118%20-10%2086%2019T53%2087Q53%20126%2074%20143T118%20160Q133%20160%20146%20151T160%20120Q160%2094%20142%2076T111%2058Q109%2057%20108%2057T107%2055Q108%2052%20115%2047T146%2034T201%2027Q237%2027%20263%2038T301%2066T318%2097T323%20122Q323%20150%20302%20164T254%20181T195%20196T148%20231Q131%20256%20131%20289Z%22%3E%3C%2Fpath%3E%0A%3C%2Fdefs%3E%0A%3Cg%20stroke%3D%22currentColor%22%20fill%3D%22currentColor%22%20stroke-width%3D%220%22%20transform%3D%22matrix(1%200%200%20-1%200%200)%22%20aria-hidden%3D%22true%22%3E%0A%3Cg%20transform%3D%22translate(40996%2C0)%22%3E%0A%3Cg%20id%3D%22mjx-eqn-1.2%22%20transform%3D%22translate(0%2C-7)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%22389%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2E%22%20x%3D%22890%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-32%22%20x%3D%221168%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%221669%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(14049%2C0)%22%3E%0A%3Cg%20transform%3D%22translate(-11%2C0)%22%3E%0A%3Cg%20transform%3D%22translate(0%2C-7)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-64%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(520%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-65%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%22466%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-64%22%20x%3D%221067%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%221590%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-65%22%20x%3D%222369%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%222835%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-64%22%20x%3D%223436%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%223698%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-4E%22%20x%3D%224754%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(5809%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-64%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(520%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-70%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%22503%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6F%22%20x%3D%22955%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-63%22%20x%3D%221440%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%222557%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(3558%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-64%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(520%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-74%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%22361%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-61%22%20x%3D%22812%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%221342%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%221943%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%226106%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(7107%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-64%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(520%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-70%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%22503%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6F%22%20x%3D%22955%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-70%22%20x%3D%221440%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%229102%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=d%7Bend-end%7D%3DN%5Cleft%28d%7Bproc%7D%2Bd%7Btrans%7D%2Bd%7Bprop%7D%5Cright%29%20%5Ctag%7B1.2%7D&id=R5nq1)
其中，dtrans = L/R，其中 L 是数据包大小。 请注意，公式 1.2 是公式 1.1 的概括，它没有考虑处理延迟和传播延迟。 在各节点具有不同的延迟和每个节点存在平均排队延迟的情况下，需要对式 1.2 进行一般化处理。我们将有关工作留给读者。

路由跟踪 Traceroute

为了亲身体验计算机网络中的端到端延迟，我们可以使用 Traceroute 程序。 Traceroute 是一个简单的程序，可以在任何 Internet 主机上运行。 当用户指定目标主机名时，源主机中的程序会向该目标发送多个特殊数据包。 当这些数据包朝着目的地前进时，它们会通过一系列路由器。 当路由器收到这些特殊数据包之一时，它会向源发回一条包含路由器名称和地址的短报文。
更具体地说，假设在源和目的地之间有 N-1 个路由器。 然后源将向网络发送 N 个特殊数据包，每个数据包都指向最终目的地。 这N个特殊数据包被标记为1到N，第一个数据包标记为1，最后一个数据包标记为N。当第n个路由器收到第n个标记为n的数据包时，路由器不会将数据包转发到目的地，而是发送一条报文回到源头。 当目标主机收到第 N 个数据包时，它也向源返回一条消息。源记录从它发送一个数据包到它收到相应的返回报文之间经过的时间； 它还记录返回消息的路由器（或目标主机）的名称和地址。 通过这种方式，源可以重构从源到目的地的数据包所采用的路由，并且源可以确定到所有中间的路由器的往返延迟。 Traceroute 实际上将刚才描述的实验重复了 3 次，因此源实际上向目的地发送了 3 • N 个数据包。 RFC 1393 详细描述了 Traceroute。
下面是Traceroute程序的输出示例，其中跟踪从源主机 gaia.c.s.umass.edu (位于马萨诸塞大学)到巴黎索邦大学计算机科学系的一个主机的路由 (以前这所大学被称为UPMC)。 输出有六列：第一列是上面描述的n值，即路由沿途的路由器编号； 第二列是路由器的名称； 第三列是路由器的地址（格式为xxx.xxx.xxx.xxx）； 最后三列是三个实验的往返延迟。 如果源从任何给定路由器收到的消息少于三个（由于网络中的数据包丢失），Traceroute 会在路由器编号后放置一个星号，并报告该路由器的往返时间少于三个。

在上面的跟踪中，源和目标之间有 14 个路由器。 这些路由器中的大多数都有名称，并且都有地址。 例如，Router 4 的名称为 core1-rt-et-5-2-0.gw.umass.edu，地址为 128.119.0.9。 查看为同一路由器提供的数据，我们看到在三个试验中的第一个中，源和路由器之间的往返延迟为 0.351 毫秒。 随后两次试验的往返延迟分别为 0.392 和 0.380 毫秒。 这些往返延迟包括刚才讨论的所有延迟，包括传输延迟、传播延迟、路由器处理延迟和排队延迟。
由于排队延迟随时间变化，发送到路由器 n 的数据包 n 的往返延迟有时可能比发送到路由器 n+1 的数据包 n+1 的往返延迟更长。 事实上，我们在上面的例子中观察到了这种现象：到路由器 12 的延迟小于到路由器 11 的延迟！ 另请注意，当从路由器 7 到路由器 8 时，往返延迟大幅增加。这是由于路由器 7 和 8 之间的跨大西洋光纤链路导致了相对较大的传播延迟。 有许多免费软件程序为 Traceroute 提供图形界面； 我们的最爱之一是 PingPlotter [PingPlotter 2020]。

终端系统，应用程序和其他延迟 End System, Application, and Other Delays

除了处理、传输和传播延迟之外，终端系统中还可能存在额外的显着延迟。 例如，想要将数据包传输到共享介质（例如，在 WiFi 或电缆调制解调器场景中）的终端系统可能会故意延迟其传输，作为与其他终端系统共享介质的协议的一部分； 我们将在第 6 章详细讨论此类协议。另一个重要的延迟是介质分组延迟（media packetization delay），它存在于 IP 语音 (VoIP) 应用程序中。 在 VoIP 中，发送方必须先用编码的数字化语音填充数据包，然后再将数据包传递到 Internet。 这次填充数据包的时间（称为打包延迟）可能很重要，并且会影响用户感知的 VoIP 呼叫质量。 这个问题将在本章末尾的家庭作业问题中进一步探讨。

1.4.4 计算机网络吞吐量 Throughput in Computer Networks

除了延迟和数据包丢失之外，计算机网络中的另一个关键性能指标是端到端吞吐量（end-to-end throughput）。 要定义吞吐量，请考虑通过计算机网络将大文件从主机 A 传输到主机 B。 例如，此传输可能是从一台计算机到另一台计算机的大型视频剪辑。 任何时刻的瞬时吞吐量（instantaneous throughput）是主机 B 接收文件的速率（以比特/秒为单位）。 （许多应用程序在用户界面中显示下载期间的瞬时吞吐量——也许您之前已经观察到了这一点！您可能想尝试使用 speedtest 应用程序 [Speedtest 2020]。）如果文件由 F 位组成并且传输需要 T 秒让主机 B 接收所有 F 位，则文件传输的平均吞吐量（average throughput）为 F/T 位/秒。 对于某些应用程序，例如 Internet 电话，希望具有始终高于某个阈值的低延迟和瞬时吞吐量（例如，某些 Internet 电话应用程序超过 24 kbps，某些实时视频应用程序超过 256 kbps）。 对于其他应用程序，包括那些涉及文件传输的应用程序，延迟并不重要，但希望具有尽可能高的吞吐量。
为了进一步了解吞吐量的重要概念，让我们考虑一些示例。 图 1.19(a) 显示了两个端系统，一个服务器和一个客户端，通过两条通信链路和一个路由器连接。 考虑从服务器到客户端的文件传输吞吐量。 让 Rs 表示服务器和路由器之间的链路速率； Rc 表示路由器和客户端之间的链路速率。 假设整个网络中唯一发送的比特是从服务器到客户端的比特。 我们现在问，在这种理想情况下，服务器到客户端的吞吐量是多少？ 为了回答这个问题，我们可以将比特视为流体，将通信链路视为管道。显然，服务器不能以比 Rs bps 更快的速率通过其链路泵送比特； 并且路由器不能以比 Rc bps 更快的速率转发比特。 如果 Rs < Rc，那么由服务器泵送的比特将“流”过路由器并以 Rs bps 的速率到达客户端，从而提供 Rs bps 的吞吐量。 另一方面，如果 Rc < Rs，则路由器将无法像接收到它们一样快速地转发比特。 在这种情况下，比特将仅以 Rc 的速率离开路由器，从而提供 Rc 的端到端吞吐量。（还要注意，如果比特继续以 Rs 的速率到达路由器，并继续以 Rc 的速率离开路由器，则路由器上等待传输到客户端的比特积压会越来越大——这是最不希望出现的情况！）因此，对于这个简单的双链路网络，吞吐量为min{Rc, Rs}，即瓶颈链路（bottleneck link）的传输速率。 确定了吞吐量后，我们现在可以将 F 位的大文件从服务器传输到客户端所需的时间近似为 F/min{Rs, Rc}。 举个具体的例子，假设你正在下载一个F=3200万比特的MP3文件，服务器的传输速率 Rs=2Mbps，你的访问链路为Rc=1Mbps。 传输文件所需的时间为 32 秒。 当然，这些吞吐量和传输时间的表达式只是近似值，因为它们没有考虑存储转发和处理延迟以及协议问题。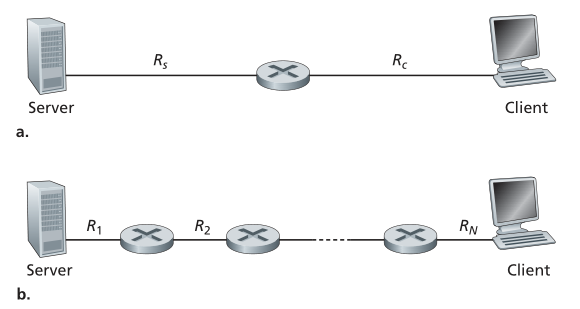

Figure 1.19 ♦ Throughput for a file transfer from server to client
图 1.19(b) 现在显示了服务器和客户端之间有 N 条链路的网络，N 条链路的传输速率为 R1, R2, … , RN。 应用与双链路网络相同的分析，我们发现从服务器到客户端的文件传输的吞吐量为 min{R1, R2, … , RN}，这又是在服务器和客户端之间沿瓶颈链路的传输速率 。
现在考虑另一个由当今互联网驱动的例子。图 1.20(a) 显示了连接到计算机网络的两个终端系统，一个服务器和一个客户端。考虑从服务器到客户端的文件传输吞吐量。服务器通过 Rs 速率的接入链路（access link）连接到网络，客户端通过 Rc 速率的接入链路连接到网络。现在假设通信网络核心的所有链路都具有非常高的传输速率，远高于Rs和Rc。事实上，今天，互联网的核心是过度供应（over-provisioned）的高速链路，几乎没有拥塞。还假设在整个网络中发送的唯一位是比特服务器到客户端的比特。因为在这个例子中计算机网络的核心就像一个宽管道，比特从源到目的地的流动速率又是 R**s 和 Rc 中的最小值，即吞吐量 = min{Rs, Rc**}。因此，当今互联网中吞吐量的限制因素通常是接入网络（access network）。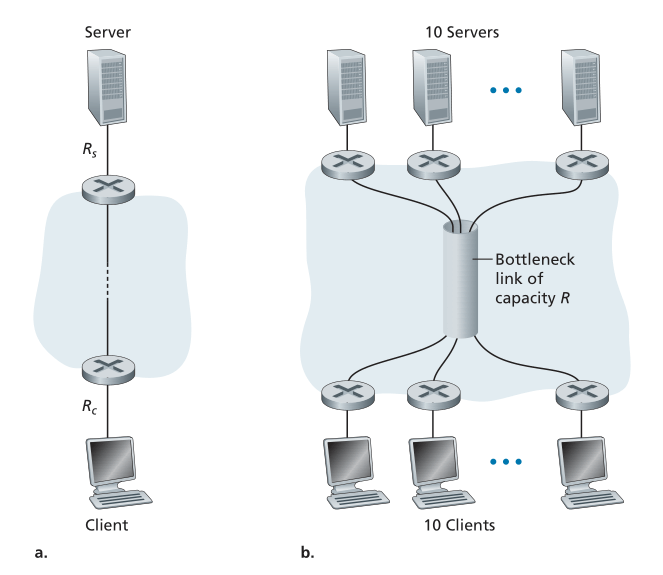

Figure 1.20 ♦ End-to-end throughput: (a) Client downloads a file from server; (b) 10 clients downloading with 10 servers
最后一个例子，请考虑图 1.20(b)，其中有 10 个服务器和 10 个客户端连接到计算机网络的核心。 在此示例中，同时进行 10 个下载，涉及 10 个客户端-服务器对。 假设这 10 次下载是当前网络中唯一的流量。 如图所示，核心中有一个链路，所有10次下载都穿过了这个链路。 用 R 表示该链路 R 的传输速率。假设所有服务器访问链路具有相同的速率 Rs，所有客户端访问链路具有相同的速率 Rc，并且核心中所有链路的传输速率——除了一个速率 R的公共链路——都远大于 Rs、Rc 和 R。现在我们问，下载的吞吐量是多少？ 显然，如果公共链路的速率 R 很大——比如说比 Rs 和 Rc 大一百倍——那么每次下载的吞吐量将再次为 min{Rs, Rc}。 但是，如果公共链路的速率与 Rs 和 Rc 的数量级相同呢？ 在这种情况下，吞吐量是多少？ 我们来看一个具体的例子。 假设 Rs = 2 Mbps，Rc = 1 Mbps，R = 5 Mbps，并且公共链路在 10 次下载之间平均分配其传输速率。 然后每次下载的瓶颈不再是接入网络，而是现在核心中的共享链路，它只为每次下载提供 500 kbps 的吞吐量。 因此，每次下载的端到端吞吐量现在减少到 500 kbps。
图 1.19 和图 1.20(a) 中的示例表明，吞吐量取决于数据流过的链路的传输速率。 我们看到，当没有其他干扰流量时，吞吐量可以简单地近似为源和目的地之间路径上的最小传输速率。 图 1.20(b) 中的示例表明，吞吐量不仅取决于路径上链路的传输速率，而且还取决于中间流量。 特别是，如果许多其他数据流也通过该链路，则具有高传输速率的链路可能仍然是文件传输的瓶颈链路。 我们将在家庭作业和后续章节中更仔细地考察计算机网络中的吞吐量。