在上一节中,我们注意到比特级错误检测和纠正-检测和纠正从一个节点发送到另一个物理连接的相邻节点的链路层帧中的比特损坏-是链路层经常提供的两项服务。我们在第3章中看到,也经常在传输层提供错误检测和纠错服务。在本节中,我们将研究几种最简单的技术,这些技术可用于检测并在某些情况下纠正此类位错误。对这一主题的理论和实现的全面论述本身就是许多教科书(例如[Schwartz 1980]或[Bertsekas 1991])的主题,我们在这里的论述必然是简短的。我们的目标是对错误检测和纠错技术提供的功能有一种直观的感觉,并了解几种简单的技术是如何工作的,以及在实践中如何在链路层中使用。<br />图6.3说明了我们研究的背景。在发送节点,用**检错和纠错比特(error-detection and -correction ,EDC)**扩充要防止比特错误的数据D。通常,要保护的数据不仅包括从网络层向下传递以通过链路传输的数据报,还包括链路帧首部中的链路级地址信息、序列号和其他字段。D和EDC都在链路级帧中发送到接收节点。在接收节点,接收比特序列D'和EDC'。请注意,由于传输中的位翻转,D'和EDC'可能与原始D和EDC不同。<br />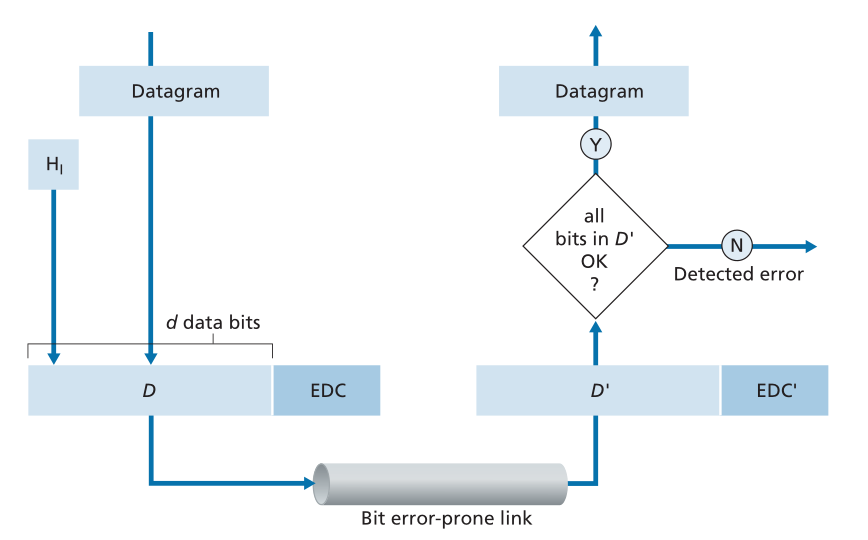<br />**Figure 6.3 ♦ Error-detection and -correction scenario**<br />**图6.3.♦错误检测和纠正场景**<br />接收方的挑战是确定D'是否与原始D'相同,因为它只接收到D'和EDC'。图6.3中接收方决定的确切措辞(我们询问是否检测到错误,而不是是否发生错误!)是很重要的。错误检测和纠错技术允许接收器有时(但不总是)检测到已经发生比特错误。即使使用检错比特,仍可能存在未检测到的比特错误;即,接收器可能不知道接收到的信息包含比特错误。因此,接收方可能会将损坏的数据报发送到网络层,或者不知道帧报头中某个字段的内容已损坏。因此,我们希望选择一种使此类事件发生的概率较小的错误检测方案。通常,更复杂的检错和纠错技术(即,那些允许未检测到的比特差错的概率较小的技术)会产生更大的开销-需要更多的计算来计算和发送更多的检错和纠错比特。<br />现在,让我们检查三种用于检测传输数据中的错误的技术-奇偶校验(parity checks,以说明错误检测和纠正背后的基本思想)、校验和方法(checksumming methods,通常用于传输层)和循环冗余校验(cyclic redundancy checks,通常用于适配器的链路层)。
6.2.1 奇偶校验 Parity Checks
也许最简单的错误检测形式是使用单个奇偶校验位(parity bit)。假设要发送的信息(图6.4中的D)具有d个比特。在偶数奇偶校验方案中,发送器简单地包括一个附加位,并选择它的值,使得d+1位(原始信息加上奇偶校验位)中的1的总数为偶数。对于奇数奇偶校验方案,选择奇偶校验位值使得存在奇数个1。图6.4说明了偶数奇偶校验方案,其中单个奇偶校验位存储在单独的字段中。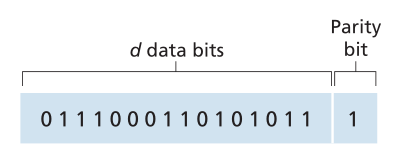
Figure 6.4 ♦ One-bit even parity
图6.4♦一位偶数奇偶校验
接收器操作也很简单,只需一个奇偶校验位。接收器只需要对接收到的d+1比特中的1进行计数。如果使用偶数奇偶校验方案发现奇数个1值位,则接收器知道至少发生了一个位错误。更准确地说,它知道发生了一些奇数个比特错误。
但是,如果出现偶数个比特错误,会发生什么情况呢?您应该说服自己,这将导致未检测到的错误。如果比特差错的概率很小,并且可以假设差错在一个比特到下一个比特之间独立地发生,则分组中的多个比特差错的概率将非常小。在这种情况下,单个奇偶校验位可能就足够了。然而,测量结果表明,错误通常以“突发(bursts)”的形式聚集在一起,而不是独立发生。在突发错误条件下,由单比特奇偶校验保护的帧中未检测到错误的概率可以接近50%[Sprigins 1991]。显然,需要一种更健壮的错误检测方案(幸运的是,在实践中使用了该方案)。但在研究实际使用的错误检测方案之前,让我们先考虑一下一位奇偶校验的简单概括,它将使我们深入了解纠错技术。
图6.5显示了单比特奇偶校验方案的二维推广。这里,D中的d个比特被分成i行和j列。为每行和每列计算奇偶校验值。得到的i+j+1个奇偶校验位包括链路层帧的检错位。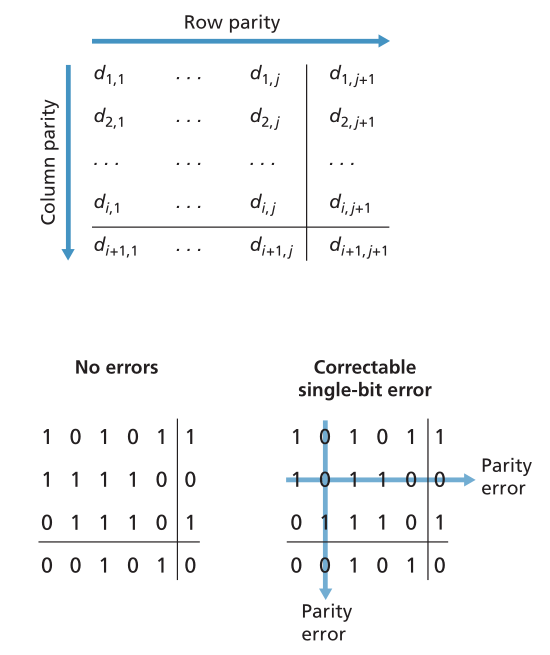
Figure 6.5 ♦ Two-dimensional even parity
图6.5♦二维偶数奇偶校验
现在假设在最初的D个信息比特中出现单个比特错误。利用这种二维奇偶校验(two-dimensional parity )方案,包含翻转比特的列和行的奇偶校验都将出错。因此,接收器不仅可以检测到发生了单个比特错误的事实,而且可以使用具有奇偶校验错误的列和行的列和行索引来实际识别损坏的比特并纠正该错误!图6.5显示了位置(2,2)中的1值位被损坏并切换为0的示例-这是一个在接收器上既可检测又可纠正的错误。虽然我们的讨论集中在最初的d个信息比特上,但是奇偶校验比特本身中的单个错误也是可检测和可纠正的。二维奇偶校验也可以检测到(但不正确!)数据包中两个错误的任意组合。二维奇偶校验方案的其他性质将在本章末尾的问题中进行探讨。
接收机检测和纠正错误的能力称为前向纠错(forward error correction,FEC)。这些技术通常用于音频存储和回放设备,例如音频CD。在网络环境中,FEC技术可以单独使用,也可以与链路层ARQ技术结合使用,类似于我们在第3章中介绍的那些技术。FEC技术很有价值,因为它们可以减少所需的发送方重新传输次数。也许更重要的是,它们允许在接收方立即纠正错误。这避免了必须等待发送方接收NAK数据包所需的往返传播延迟以及重发的数据包传播回接收方-这对于具有长传播延迟的实时网络应用(Rubenstein 1998)或链路(例如深空链路)来说是潜在的重要优势。研究在差错控制协议中使用FEC的研究包括[Biersack 1992;Nonnenmacher 1998;Byers 1998;Shacham 1990]。
6.2.2 校验和方法 Checksumming Methods
在校验和技术中,图6.4中的d位数据被视为k位整数序列。一种简单的校验和方法是简单地对这些k位整数求和,并将得到的和用作检错位。Internet校验和基于此方法-将数据字节视为16位整数并求和。然后,此和的1补码构成段首部中携带的Internet校验和。如第3.3节所述,接收器通过取接收数据(包括校验和)和的1补码并检查结果是否全为0位来检查校验和。如果任一位为1,则指示错误。RFC 1071详细讨论了Internet校验和算法及其实现。在TCP和UDP协议中,对所有字段(包括首部和数据字段)计算Internet校验和。在IP中,校验和是在IP首部上计算的(因为UDP或TCP数据段有自己的校验和)。在其他协议中,例如XTP[Strayer 1992],在首部上计算一个校验和,在整个数据包上计算另一个校验和。
校验和方法需要相对较小的数据包开销。例如,TCP和UDP中的校验和仅使用16位。然而,与循环冗余校验相比,它们提供的差错保护相对较弱,循环冗余校验将在下面讨论,并且通常在链路层中使用。此时的一个自然问题是,为什么在传输层使用校验和,在链路层使用循环冗余校验?回想一下,传输层通常在主机中的软件中实现,作为主机操作系统的一部分。由于传输层错误检测是在软件中实现的,因此拥有简单快速的错误检测方案(如校验和)非常重要。另一方面,链路层的错误检测在适配器中的专用硬件中实现,可以快速执行更复杂的CRC操作。Feldmeier[Feldmeier 1995]不仅给出了加权校验和码的快速软件实现技术,而且还给出了CRC(见下文)和其他码的快速软件实现技术。
6.2.3 循环冗余校验 Cyclic Redundancy Check (CRC)
当今计算机网络中广泛使用的检错技术是基于循环冗余校验(CRC)码(cyclic redundancy check (CRC) codes)。CRC码也称为多项式码(polynomial codes),因为可以将要发送的比特串视为其系数是比特串中的0和1值的多项式,对该比特串的运算解释为多项式算术(polynomial arithmetic)。
CRC码的工作方式如下。考虑发送节点想要发送到接收节点的d比特数据段D。发送方和接收方必须首先商定r+1位模式,称为生成器(generator),我们将表示为G。我们将要求G的最高有效位(最左边)为1。CRC码背后的关键思想如图6.6所示。对于给定的数据段D,发送器将选择r个附加位R,并将它们附加到D上,使得得到的d+r位模式(解释为二进制数)可使用模2运算精确地被G整除(即,没有余数)。因此,利用CRC进行差错校验的过程很简单:接收器将D+R个接收比特除以G。如果余数不为零,则接收器知道发生了错误;否则,数据被认为是正确的。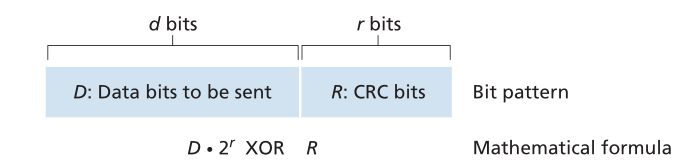
Figure 6.6 ♦ CRC
图6.6♦循环冗余校验
所有CRC计算都以模2运算完成,没有加法进位或在减法中借用。这意味着加法和减法是相同的,并且两者都等同于操作数的按位异或(XOR)。因此,例如,
1011 XOR 0101 = 1110
1001 XOR 1101 = 0100
同样,我们也有类似的
1011 - 0101 = 1110
1001 - 1101 = 0100
乘法和除法与以2为基的算术相同,不同之处在于任何必需的加法或减法都是在没有进位或借位的情况下完成的。与常规二进制算术一样,乘以2k将位模式左移k位。因此,给定D和R,量D×2r XOR R产生如图6.6所示的d+r位模式。在下面的讨论中,我们将使用图6.6中的d+r位模式的代数特征。
现在让我们转到关键问题,即发送方如何计算R。请记住,我们希望找到R,这样就有n,即
也就是说,我们希望选择R,这样G除以D×2r XOR R,没有余数。如果我们对上述等式的两边进行异或运算(即,将模2相加,不带进位)R,我们将得到
这个等式告诉我们,如果我们把D×2r除以G,余数的值正好是R。换句话说,我们可以把R计算为
图6.7说明了D=101110、d=6、G=1001和r=3的情况下的计算。在这种情况下传输的9位是10111011。您应该自己检查这些计算,并检查D×2r=101011×G XOR R。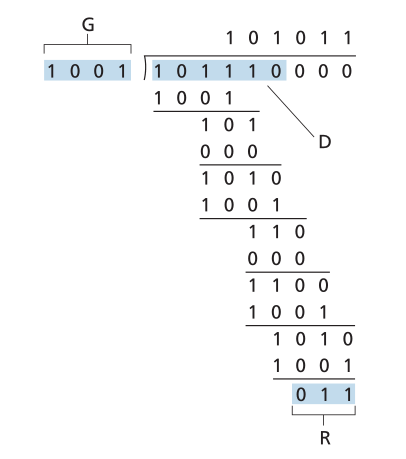
Figure 6.7 ♦ A sample CRC calculation
图6.7♦CRCA示例计算
已经为8位、12位、16位和32位生成器定义了国际标准G。已经在许多链路级IEEE协议中采用的CRC-32 32位标准使用
每个CRC标准可以检测少于r+1比特的突发错误。(这意味着将检测到r比特或更少的所有连续比特差错。)。此外,在适当的假设下,以1-0.5r的概率检测到长度大于r+1比特的突发。此外,每个CRC标准都可以检测任何奇数个比特错误。有关实施CRC校验的讨论,请参见[Williams 1993]。CRC码和更强大的码背后的理论超出了本文的范围。文本[Schwartz 1980]为这个主题提供了一个很好的介绍。

