题目描述：

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？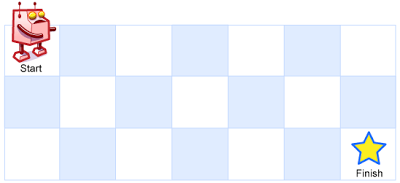
不同路径 - 图1
例如，上图是一个7 x 3 的网格。有多少可能的路径？
说明：m 和 n 的值均不超过 100。
示例 1:**

  1. 输入: m = 3, n = 2
  2. 输出: 3
  3. 解释:
  4. 从左上角开始，总共有 3 条路径可以到达右下角。
  5. 1. 向右 -> 向右 -> 向下
  6. 2. 向右 -> 向下 -> 向右
  7. 3. 向下 -> 向右 -> 向右

示例 2:

  1. 输入: m = 7, n = 3
  2. 输出: 28

算法实现：

  1. /**
  2.  * @param {number} m
  3.  * @param {number} n
  4.  * @return {number}
  5.  */
  6. var uniquePaths = (m, n) => {
  7.     var factorial = (m, n) => {
  8.         var num = 1
  9.         var count = 0
  10.         for(var i = m; i > 0; i-- ) {
  11.             if (count === n) {
  12.                 break
  13.             }
  14.             num = num * i
  15.             count++
  16.         }
  17.         return num
  18.     }
  19.     return factorial(m + n - 2, m - 1)/factorial(m - 1, m - 1)
  20. };

思考：

以前做过的排列组合题目，也可以应用动态规划法解题。

总结：

动态规划法还没有看懂，一会再理解一下。