AdaBoost

1、计算样本权重
训练数据中的每个样本，赋予其权重，即样本权重，用向量D表示，这些权重都初始化成相等值。假设有n个样本的训练集：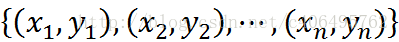

设定每个样本的权重都是相等的，即1/n。

2、计算错误率
利用第一个弱学习算法h1对其进行学习，学习完成后进行错误率ε的统计：

3、计算弱学习算法权重
弱学习算法也有一个权重，用向量α表示，利用错误率计算权重α：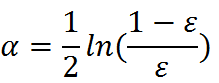

4、更新样本权重
在第一次学习完成后，需要重新调整样本的权重，以使得在第一分类中被错分的样本的权重，在接下来的学习中可以重点对其进行学习：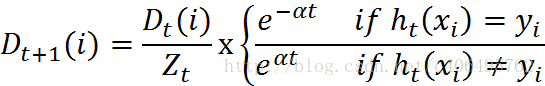

其中，h_t(x_i) = y_i表示对第i个样本训练正确，不等于则表示分类错误。Z_t是一个归一化因子：

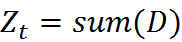
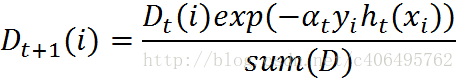
5、AdaBoost算法
重复进行学习，这样经过t轮的学习后，就会得到t个弱学习算法、权重、弱分类器的输出以及最终的AdaBoost算法的输出，分别如下：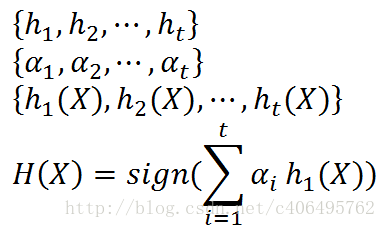

def loadSimpData():
    datMat = np.matrix([[ 1. ,  2.1],
        [ 1.5,  1.6],
        [ 1.3,  1. ],
        [ 1. ,  1. ],
        [ 2. ,  1. ]])
    classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
    return datMat,classLabels
def showDataSet(dataMat, labelMat):
data_plus = []                                  #正样本
    data_minus = []                                 #负样本
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    data_plus_np = np.array(data_plus)                                             #转换为numpy矩阵
    data_minus_np = np.array(data_minus)                                         #转换为numpy矩阵
    plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1])        #正样本散点图
    plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1])     #负样本散点图
    plt.show()
if __name__ == '__main__':
    dataArr,classLabels = loadSimpData()
    showDataSet(dataArr,classLabels)

def loadSimpData():
     datMat = np.matrix([[ 1. ,  2.1],
        [ 1.5,  1.6],
        [ 1.3,  1. ],
        [ 1. ,  1. ],
        [ 2. ,  1. ]])
    classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
    return datMat,classLabels
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):
retArray = np.ones((np.shape(dataMatrix)[0],1))                #初始化retArray为1
    if threshIneq == 'lt':
        retArray[dataMatrix[:,dimen] <= threshVal] = -1.0         #如果小于阈值,则赋值为-1
    else:
        retArray[dataMatrix[:,dimen] > threshVal] = -1.0         #如果大于阈值,则赋值为-1
    return retArray
def buildStump(dataArr,classLabels,D):
 dataMatrix = np.mat(dataArr); labelMat = np.mat(classLabels).T
    m,n = np.shape(dataMatrix)
    numSteps = 10.0; bestStump = {}; bestClasEst = np.mat(np.zeros((m,1)))
    minError = float('inf')                                                        #最小误差初始化为正无穷大
    for i in range(n):                                                            #遍历所有特征
        rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max()        #找到特征中最小的值和最大值
        stepSize = (rangeMax - rangeMin) / numSteps                                #计算步长
        for j in range(-1, int(numSteps) + 1):                                     
            for inequal in ['lt', 'gt']:                                          #大于和小于的情况，均遍历。lt:less than，gt:greater than
                threshVal = (rangeMin + float(j) * stepSize)                     #计算阈值
                predictedVals = stumpClassify(dataMatrix, i, threshVal, inequal)#计算分类结果
                errArr = np.mat(np.ones((m,1)))                                 #初始化误差矩阵
                errArr[predictedVals == labelMat] = 0                             #分类正确的,赋值为0
                weightedError = D.T * errArr                                      #计算误差
                print("split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (i, threshVal, inequal, weightedError))
                if weightedError < minError:                                     #找到误差最小的分类方式
                    minError = weightedError
                    bestClasEst = predictedVals.copy()
                    bestStump['dim'] = i
                    bestStump['thresh'] = threshVal
                    bestStump['ineq'] = inequal
    return bestStump,minError,bestClasEst
if __name__ == '__main__':
    dataArr,classLabels = loadSimpData()
    D = np.mat(np.ones((5, 1)) / 5)
    bestStump,minError,bestClasEst = buildStump(dataArr,classLabels,D)
    print('bestStump:\n', bestStump)
    print('minError:\n', minError)
    print('bestClasEst:\n', bestClasEst)

def loadSimpData():
    datMat = np.matrix([[ 1. ,  2.1],
        [ 1.5,  1.6],
        [ 1.3,  1. ],
        [ 1. ,  1. ],
        [ 2. ,  1. ]])
    classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
    return datMat,classLabels
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):
 retArray = np.ones((np.shape(dataMatrix)[0],1))                #初始化retArray为1
    if threshIneq == 'lt':
        retArray[dataMatrix[:,dimen] <= threshVal] = -1.0         #如果小于阈值,则赋值为-1
    else:
        retArray[dataMatrix[:,dimen] > threshVal] = -1.0         #如果大于阈值,则赋值为-1
    return retArray
def buildStump(dataArr,classLabels,D):
dataMatrix = np.mat(dataArr); labelMat = np.mat(classLabels).T
    m,n = np.shape(dataMatrix)
    numSteps = 10.0; bestStump = {}; bestClasEst = np.mat(np.zeros((m,1)))
    minError = float('inf')                                                        #最小误差初始化为正无穷大
    for i in range(n):                                                            #遍历所有特征
        rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max()        #找到特征中最小的值和最大值
        stepSize = (rangeMax - rangeMin) / numSteps                                #计算步长
        for j in range(-1, int(numSteps) + 1):                                     
            for inequal in ['lt', 'gt']:                                          #大于和小于的情况，均遍历。lt:less than，gt:greater than
                threshVal = (rangeMin + float(j) * stepSize)                     #计算阈值
                predictedVals = stumpClassify(dataMatrix, i, threshVal, inequal)#计算分类结果
                errArr = np.mat(np.ones((m,1)))                                 #初始化误差矩阵
                errArr[predictedVals == labelMat] = 0                             #分类正确的,赋值为0
                weightedError = D.T * errArr                                      #计算误差
                print("split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (i, threshVal, inequal, weightedError))
                if weightedError < minError:                                     #找到误差最小的分类方式
                    minError = weightedError
                    bestClasEst = predictedVals.copy()
                    bestStump['dim'] = i
                    bestStump['thresh'] = threshVal
                    bestStump['ineq'] = inequal
    return bestStump, minError, bestClasEst
def adaBoostTrainDS(dataArr, classLabels, numIt = 40):
    weakClassArr = []
    m = np.shape(dataArr)[0]
    D = np.mat(np.ones((m, 1)) / m)                                            #初始化权重
    aggClassEst = np.mat(np.zeros((m,1)))
    for i in range(numIt):
        bestStump, error, classEst = buildStump(dataArr, classLabels, D)     #构建单层决策树
        print("D:",D.T)
        alpha = float(0.5 * np.log((1.0 - error) / max(error, 1e-16)))         #计算弱学习算法权重alpha,使error不等于0,因为分母不能为0
        bestStump['alpha'] = alpha                                          #存储弱学习算法权重
        weakClassArr.append(bestStump)                                      #存储单层决策树
        print("classEst: ", classEst.T)
        expon = np.multiply(-1 * alpha * np.mat(classLabels).T, classEst)     #计算e的指数项
        D = np.multiply(D, np.exp(expon))                                      
        D = D / D.sum()                                                        #根据样本权重公式，更新样本权重
        #计算AdaBoost误差，当误差为0的时候，退出循环
        aggClassEst += alpha * classEst                                 
        print("aggClassEst: ", aggClassEst.T)
        aggErrors = np.multiply(np.sign(aggClassEst) != np.mat(classLabels).T, np.ones((m,1)))     #计算误差
        errorRate = aggErrors.sum() / m
        print("total error: ", errorRate)
        if errorRate == 0.0: break                                             #误差为0，退出循环
    return weakClassArr, aggClassEst
if __name__ == '__main__':
    dataArr,classLabels = loadSimpData()
    weakClassArr, aggClassEst = adaBoostTrainDS(dataArr, classLabels)
    print(weakClassArr)
    print(aggClassEst)