题目描述：

给定 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明：你不能倾斜容器，且 n 的值至少为 2。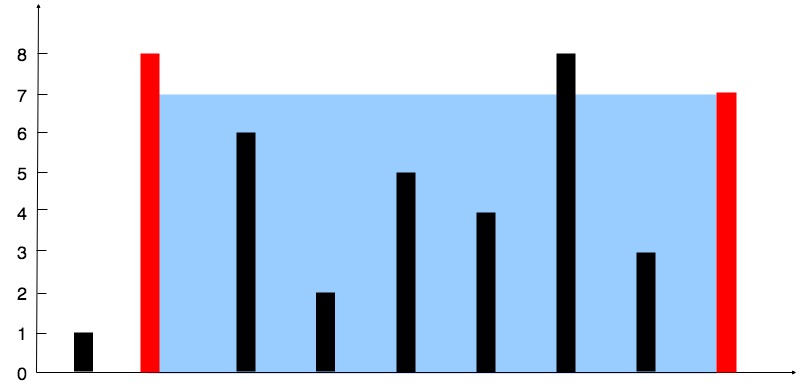
盛最多水的容器 - 图1
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。
**示例:

  1. 输入: [1,8,6,2,5,4,8,3,7]
  2. 输出: 49

算法实现：

JavaScript

  1. /**
  2.  * @param {number[]} height
  3.  * @return {number}
  4.  */
  5. var maxArea = function(height) {
  6.     var maxWater = 0
  7.     for (var i = 0; i < height.length - 1; i++ ) {
  8.         for (var j = i + 1; j < height.length; j++ ) {
  9.             maxWater = Math.min(height[i], height[j]) * (j - i) > maxWater ? Math.min(height[i], height[j]) * (j - i) : maxWater
  10.         }
  11.     }
  12.     return maxWater
  13. };

思考：

依据木桶原理，最短的板代表盛水的多少，所以，此题中盛水的多少就是（j-i）* j和i中的最小值，应用Math.min（）方法求出最小值，循环比较即可。

总结：

使用了以前很少使用的Math.min（）方法，双循环套用很简单的解决了这个问题，但是代码的时间复杂度还有待提高。