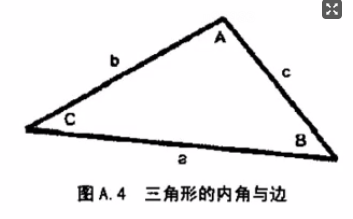
余弦定理： （与向量点乘有关） a2 = b2 + c2 - 2bc cosA b2 = a2 + c2 - 2bc cosB c2 = a2 + c2 - 2bc cosC
余弦定理推导
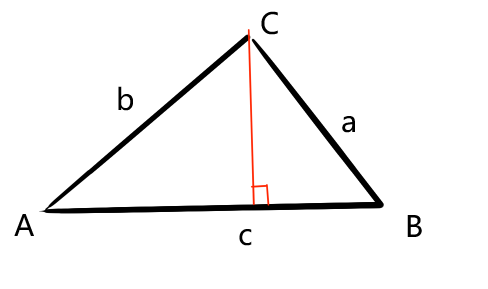
| 已知 角B 边a、c 求边b |
 |
|---|---|
| 设 垂直于c的高h 短边长x 则另一边c-x 由勾股定理可列出高度h的表达式组 h²=a²-x² h²=b²-(c-x)² 即 a²-x² = b²-(c-x)² 化简 x=（a²+c²-b²）/ 2c |
 |
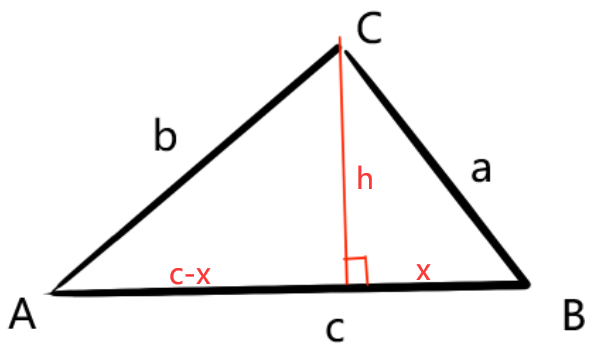| 由三角函数可知 cosB=x/a 带入x即可导出余弦定理 b²=a²+b²-2accosB |
若有收获，就点个赞吧
0 人点赞
