点乘：dot product

点乘：dot

运算公式：A·B = xaxb + yayb = |a||b|cosθ
（分量相乘相加）
（θ是两向量夹角，0-Π之间）
运算方式：向量 · 向量
运算结果：标量
————————————————————————————-
几何意义：标量值用于反三角函数求取 两向量的夹角（或者判断钝角还是锐角）
=0 两向量垂直
<0 小于零为钝角
>0 大于零为锐角

具体的点乘几何意义要在线性变换中才能体现出来

点乘原理

两向量互相投影长

已知 2向量A、B， 模长分别为a、b 两向量夹角为 α 求这两个向量分别在对方身上的投影长度L**1和L**2
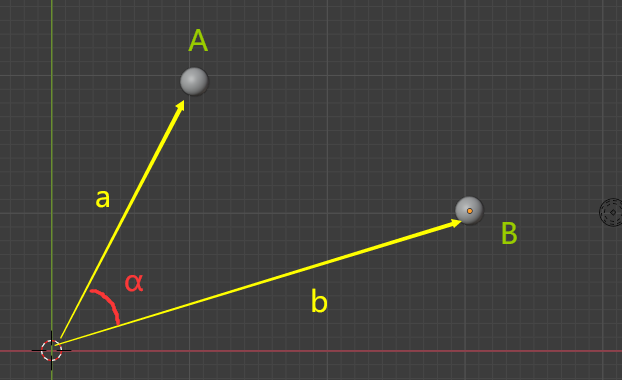向量A在向量B上的投影 cosα=L1/a L**1*= a cosα
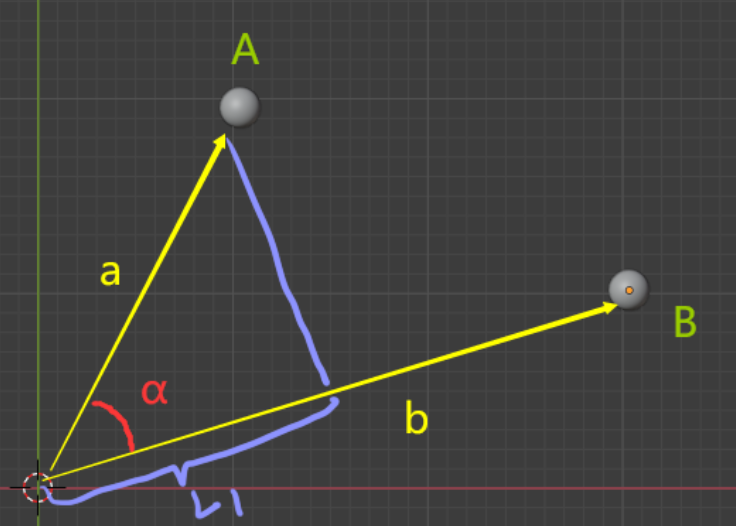向量A在向量B上的投影 cosα=L2/b L**2*=a cosα	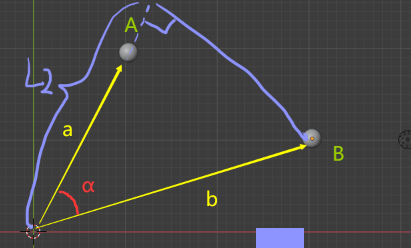没画直…

点乘公式推导

已知 向量A、B，及其夹角α A=（Xa，Ya） B=（Xb，Yb）
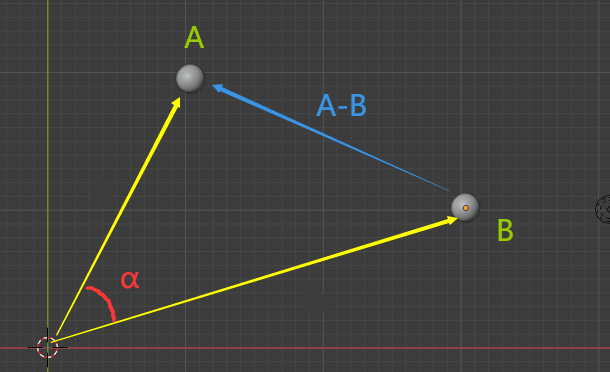由余弦定理可求取，三角形的第三边 |A-B|² = |A|² + |B|² - 2|A||B|cosα	【其中 2|A||B|cosα，和向量的投影长很像】
由余弦定理变形 |A||B|cosα = 1/2 (|A|² + |B|² - |A-B|²)
带入向量分量，化简就是点乘 |A||B|cosα = xaxb + yayb