向量的模长

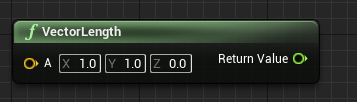
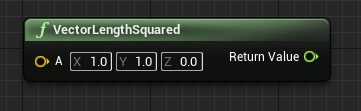
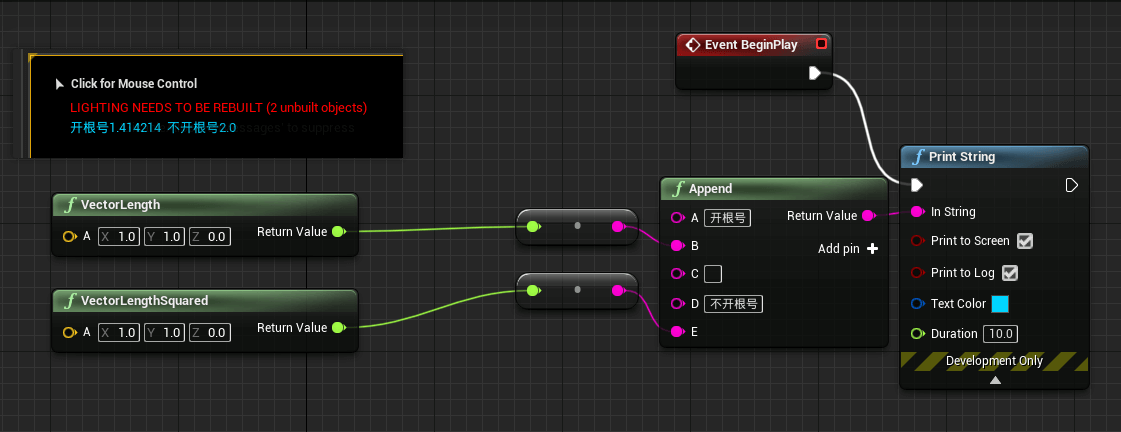
向量的模长

几何意义：模长表示向量的长度
向量： A=(x, y, z)
模长公式：|A| =
求解方式：勾股定理

应用：计算2点之间的距离
应用2：向量归一化（将向量长度变为1）

UE4求取模长

模长（开根号，值会有误差） |A| =

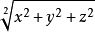
模长的平方（不开根号，保证值的正确性） |A|2 =x2+y2+z2 （数值比较，一搬用这种方式，1准确、2更快）

向量归一化

标准化、归一化、规范化、单位化都表示一个意思 向量归一化本质是标量乘法

计算公式：向量÷模长
注意：模长不能为0，（归一化之前需要检查模长）

UE4归一化函数

2D归一化		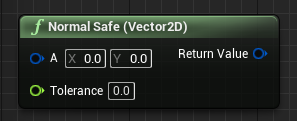安全归一化	向量长度小于（Tolerance）时 返回0 当向量长度大于（Tolerance）时 返回1（模长）
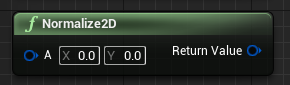		归一化	向量长度小于0.000000001时 返回0 当向量长度大于0.000000001时 返回1（模长）
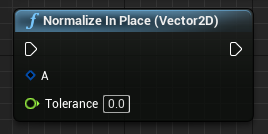		原地归一化	向量长度小于（Tolerance）时 向量被修改为0 当向量长度大于（Tolerance）时 向量被修改为1（模长）
3D归一化		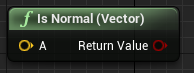检查是否归一化	检查模长是否为1
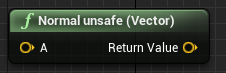		不安全的归一化	不检查模长，直接进行归一化 （当0向量进行归一化时，会出错）
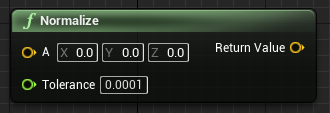		归一化	向量长度小于（Tolerance）时 不进行归一化 当向量长度大于（Tolerance）时 返回1（模长）
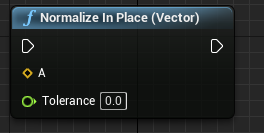		原地归一化	向量长度小于（Tolerance）时 返回0 当向量长度大于（Tolerance）时 返回1（模长）
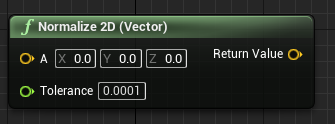		抛弃Z轴进行归一化	向量长度小于（Tolerance）时 返回0 当向量长度大于等于（Tolerance）时 返回1（模长）

应用：求取目的地坐标

条件：已知移动的方向的向量N(归一化)，移动距离a，出发点向量(点)A， 求目的地向量(点)B 公式：B=aN+A

常用计算：向前移动

常用计算：朝任意角度移动

需要将角度转化为向量，并归一化 A向量：上图的那个点 m向量：移动方向（归一化） k标量：移动距离 B向量：移动的目的地（需要求取的点）
计算公式：B=km+B 应用：求取目的地，力的方向，速度方向