求取【两向量】夹角

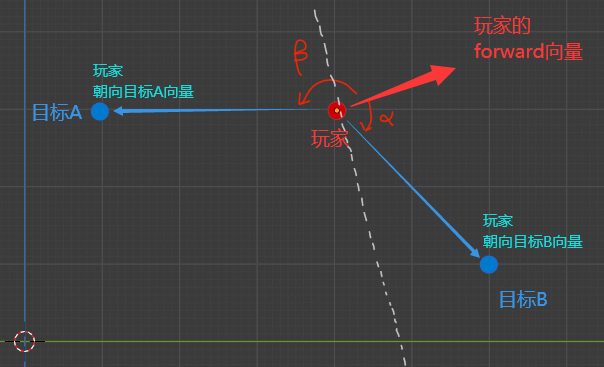
点乘应用

已知条件

已知玩家、目标A、目标B的坐标
已知玩家朝前向量（forward）玩F（局部坐标轴的X方向）

分别求取玩家分别与向量A、向量B的夹角α、β

求解

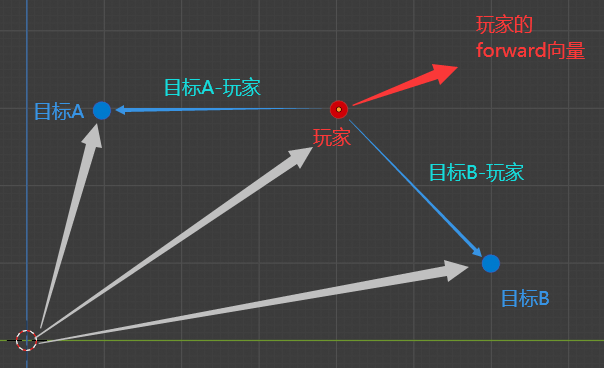
由向量减法可得 玩家到目标的向量，到A和到B 到A = 目标A坐标 - 玩家坐标 到B = 目标B坐标 - 玩家坐标
分别对 到A、到B向量进行归一化操作 Normal(到A) = 到A÷|到A| Normal(到B) = 到B÷|到B|

玩家朝前向量（forward）
玩F 默认已经归一化了 | | | 使用点乘运算：|A||B|cosα = xaxb + yayb
|玩F| * |Normal(到A)| * cosα = x**F**xNormal(到A) + y**F**yNormal(到A)
|玩F| * |Normal(到B)| * cosβ = x**F**xNormal(到B) + y**F**yNormal(到B)
衍生结果：
当夹角大于90° 点乘结果小于0
当夹角等于90°点乘结果等于0
当夹角小于90°点乘结果大于0

由于向量都已经归一化（即模长为1），所以余弦函数
cosα = x**F**xNormal(到A) + y**F**yNormal(到A)
cosβ = x**F**xNormal(到B) + y**F**yNormal(到B)

| | | 由反三角函数可得角度
α = arccos（cosα）
β = arccos（cosβ）
| |

UE4实际操作

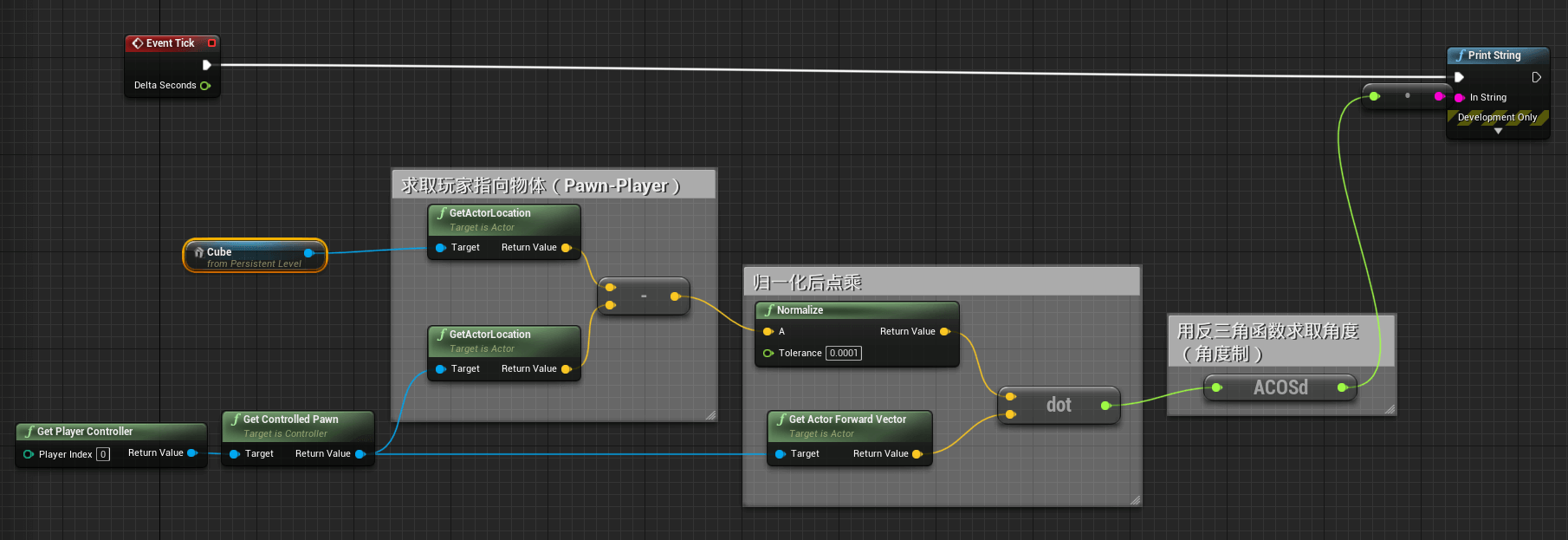
操作注意事项

注意：可以通过【DrawDebugArrow】来连接2坐标点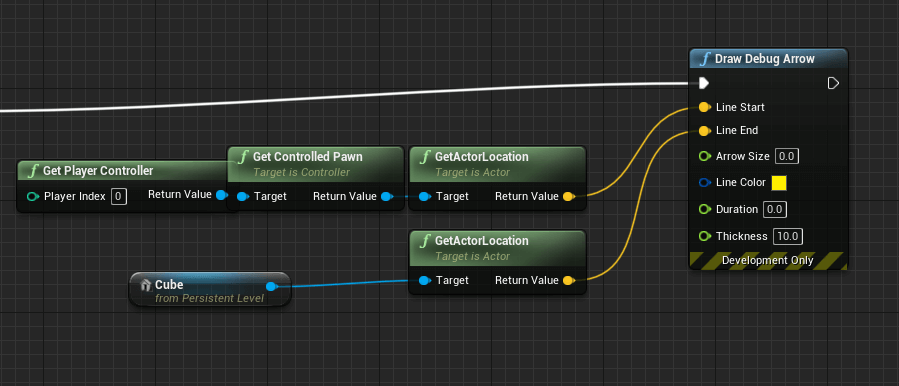

注意：
可以给角色添加一个箭头组件方便观察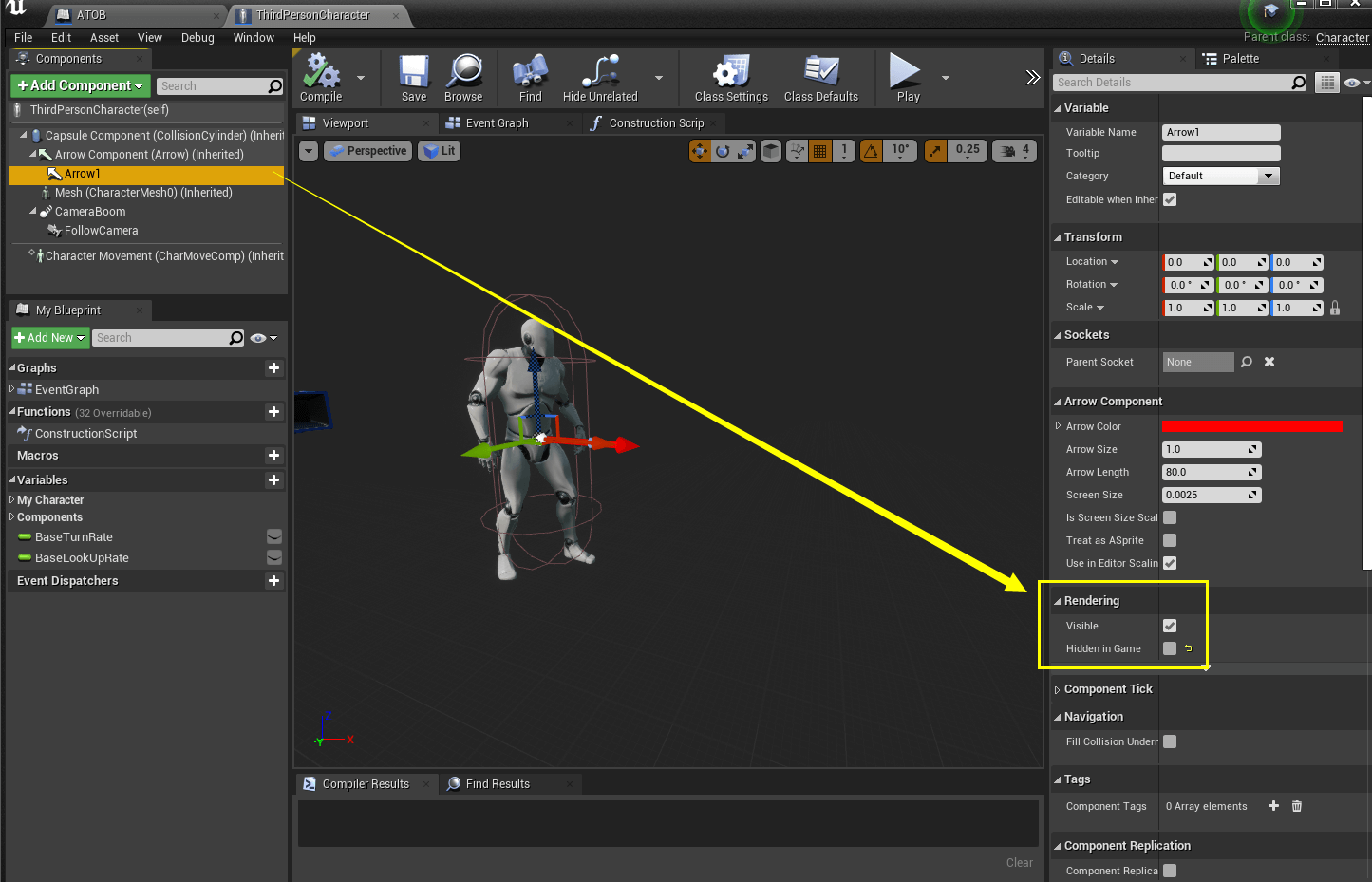

黄色连线和红色箭头的夹角