| 406. 根据身高重建队列 | 方法一:贪心+插入 方法二:树状数组 |
类似于AcWing 244. 谜一样的牛 前者已知身高和排在前面的数量求位置 后者已知位置和排在前面的数量求身高 |
|---|---|---|
| 315. 计算右侧小于当前元素的个数 | 方法一:树状数组 方法二:归并 |
类似于剑指 Offer 51. 数组中的逆序对 区别在于后者是整体逆序对数量,前者是针对具体某个元素而言的,归并实现时细节有所区别 |
| 327. 区间和的个数 | 方法一:离散化+树状数组 方法二:归并 |
又是一道利用归并的中间过程的题! |
| 493. 翻转对 | 方法一:离散化+树状数组 方法二:归并 |
|
| AcWing 1215. 小朋友排队 | 方法一:树状数组 方法二:归并 |
从单个元素着手 |
406. 根据身高重建队列
思路:
方法1:从高到低考虑
重新排序,按照身高从大到小,相同身高的按照排在前面的人数从小到大排。
考虑到总人数只有2000,可以在O(n2)时间复杂度内暴力插入解决。
从前往后根据相对关系将每个人插入到队列中
方法2:从低到高考虑
重新排序,按照身高从小到大,相同身高按照排在前面的人数从大到小排。
从前往后将每个人置于他应该在的位置
实现1:暴力寻找每个人应在的位置
实现2:使用二分+ 树状数组优化求解每个人应在的位置
// 从高到低考虑class Solution {public int[][] reconstructQueue(int[][] people) {List<Integer> list = new LinkedList<>();Arrays.sort(people, (o1, o2) -> (o1[0] == o2[0] ? o1[1] - o2[1] : o2[0] - o1[0]));int n = people.length;for (int i = 0; i < n; i++) {int idx = people[i][1];list.add(idx, i);}int[][] res = new int[n][2];int i = 0;for (int idx : list) {res[i++] = people[idx];}return res;}}
// 从低到高考虑,使用暴力插入class Solution {public int[][] reconstructQueue(int[][] people) {int n = people.length;Arrays.sort(people, (o1, o2) -> (o1[0] == o2[0] ? o2[1] - o1[1] : o1[0] - o2[0]));int[] a = new int[n];Arrays.fill(a, -1);int idx = 0;for (int[] p : people) {int h = p[0], c = p[1];int cnt = 0;int i = 0;while (cnt < c) {if (a[i] == -1)cnt++;i++;}while (a[i] != -1)i++;a[i] = idx++;}int[][] res = new int[n][];for (int i = 0; i < n; i++) {res[i] = people[a[i]];}return res;}}
// 从低到高考虑,使用二分 + 树状数组优化class Solution {public int[][] reconstructQueue(int[][] people) {int n = people.length;Arrays.sort(people, (o1, o2) -> (o1[0] == o2[0] ? o2[1] - o1[1] : o1[0] - o2[0]));BIT bit = new BIT(n);bit.init();int[][] res = new int[n][2];for (int i = 0; i < n; i++) {int h = people[i][0], k = people[i][1];int t = k + 1;int l = 1, r = n;while (l < r) {int mid = l + r >> 1;if (bit.sum(mid) < t)l = mid + 1;elser = mid;}res[l - 1] = people[i];bit.add(l, -1);}return res;}}class BIT {int n;int[] a;BIT(int n) {this.n = n;a = new int[n + 1];}void init() {for (int i = 1; i <= n; i++)a[i] = i & (-i);}void add(int idx, int x) {for (int i = idx ; i <= n; i += i & (-i))a[i] += x;}int sum(int idx) {int res = 0;for (int i = idx; i > 0; i -= i & (-i))res += a[i];return res;}}
时间复杂度分析:
前两种都是O(n2)的
用树状数组复杂度为O(nlognlogn)
AcWing 244. 谜一样的牛
思路:
倒着遍历,相当于已知当前奶牛在所有可选高度中属于第几小。
用树状数组维护当前剩余可选高度,边维护边求解
时间复杂度:O(nlognlogn)
import java.util.*;public class Main {static final int N = 100010;static int n;static int[] a = new int[N], res = new int[N];static BIT bit = new BIT(N);public static void main(String[] args) {Scanner sc = new Scanner(System.in);bit.init();n = sc.nextInt();for (int i = 2; i <= n; i++)a[i] = sc.nextInt();for (int i = n; i >= 1; i--) {int x = a[i] + 1;int l = 1, r = n;while (l < r) {int mid = l + r >> 1;if (bit.sum(mid) < x)l = mid + 1;elser = mid;}res[i] = l;bit.add(l, -1);}for (int i = 1; i <= n; i++)System.out.println(res[i]);}}class BIT {int n;int[] a;BIT(int n) {this.n = n;a = new int[n + 1];}void init() {for (int i = 1; i <= n; i++)a[i] = lowbit(i);}void add(int idx, int x) {for (int i = idx; i <= n; i += lowbit(i))a[i] += x;}int sum(int idx) {int res = 0;for (int i = idx; i > 0; i -= lowbit(i))res += a[i];return res;}int lowbit(int x) {return x & (-x);}}
308. 二维区域和检索 - 可变
给你一个二维矩阵 matrix ,你需要处理下面两种类型的若干次查询:
- 更新:更新 matrix 中某个单元的值。
- 求和:计算矩阵 matrix 中某一矩形区域元素的 和 ,该区域由 左上角 (row1, col1) 和 右下角 (row2, col2) 界定。
实现 NumMatrix 类:
- NumMatrix(int[][] matrix) 用整数矩阵 matrix 初始化对象。
- void update(int row, int col, int val) 更新 matrix[row][col] 的值到 val 。
- int sumRegion(int row1, int col1, int row2, int col2) 返回矩阵 matrix 中指定矩形区域元素的 和 ,该区域由 左上角 (row1, col1) 和 右下角 (row2, col2) 界定。
示例 1:
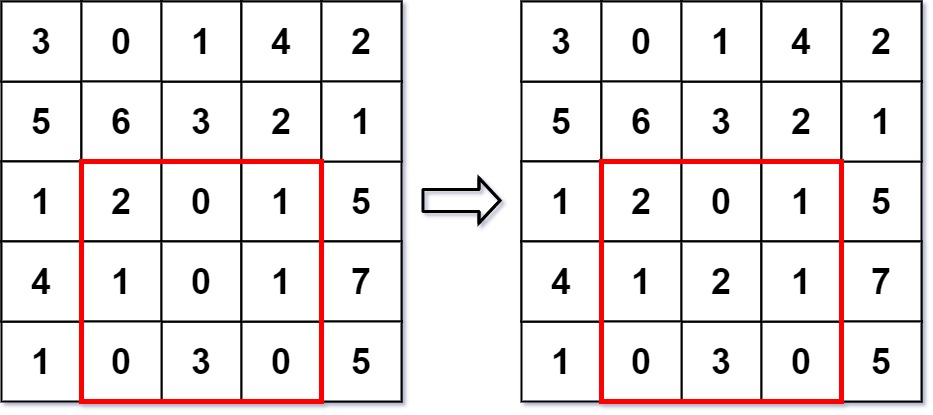
输入 [“NumMatrix”, “sumRegion”, “update”, “sumRegion”] [[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [3, 2, 2], [2, 1, 4, 3]] 输出 [null, 8, null, 10] 解释 NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]); numMatrix.sumRegion(2, 1, 4, 3); // 返回 8 (即, 左侧红色矩形的和) numMatrix.update(3, 2, 2); // 矩阵从左图变为右图 numMatrix.sumRegion(2, 1, 4, 3); // 返回 10 (即,右侧红色矩形的和)
提示:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 200
- -105 <= matrix[i][j] <= 105
- 0 <= row < m
- 0 <= col < n
- -105 <= val <= 105
- 0 <= row1 <= row2 < m
- 0 <= col1 <= col2 < n
- 最多调用104 次 sumRegion 和 update 方法
思路:
二维树状数组
class NumMatrix {int n, m;int[][] a;private int lowbit(int x) {return x & (-x);}public NumMatrix(int[][] g) {this.n = g.length;this.m = g[0].length;a = new int[n + 1][m + 1];// 注意初始化,先列后行,不能同时更新for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {a[i][j] += g[i - 1][j - 1];int j2 = j + lowbit(j), i2 = i + lowbit(i);if (j2 <= m)a[i][j2] += a[i][j];}}for (int i = 1; i <= n; i++) {int i2 = i + lowbit(i);if (i2 > n) continue;for (int j = 1; j <= m; j++) {a[i2][j] += a[i][j];}}}public void update(int row, int col, int val) {val -= sumRegion(row, col, row, col);row++;col++;add(row, col, val);}private void add(int row, int col, int val) {for (int i = row; i <= n; i += lowbit(i)) {for (int j = col; j <= m; j += lowbit(j)) {a[i][j] += val;}}}private int sum(int row, int col) {int res = 0;for (int i = row; i > 0; i -= lowbit(i)) {for (int j = col; j > 0; j -= lowbit(j)) {res += a[i][j];}}return res;}public int sumRegion(int row1, int col1, int row2, int col2) {row1++;row2++;col1++;col2++;return sum(row2, col2) - sum(row2, col1 - 1) - sum(row1 - 1, col2) + sum(row1 - 1, col1 - 1);}}/*** Your NumMatrix object will be instantiated and called as such:* NumMatrix obj = new NumMatrix(matrix);* obj.update(row,col,val);* int param_2 = obj.sumRegion(row1,col1,row2,col2);*/
class NumMatrix {int n, m;int[][] a;private int lowbit(int x) {return x & (-x);}public NumMatrix(int[][] g) {this.n = g.length;this.m = g[0].length;a = new int[n + 1][m + 1];// 用更新的方式初始化for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {add(i, j, g[i - 1][j - 1]);}}// for (int i = 1; i <= n; i++) {// int i2 = i + lowbit(i);// if (i2 > n) continue;// for (int j = 1; j <= m; j++) {// a[i2][j] += a[i][j];// }// }}public void update(int row, int col, int val) {val -= sumRegion(row, col, row, col);row++;col++;add(row, col, val);}private void add(int row, int col, int val) {for (int i = row; i <= n; i += lowbit(i)) {for (int j = col; j <= m; j += lowbit(j)) {a[i][j] += val;}}}private int sum(int row, int col) {int res = 0;for (int i = row; i > 0; i -= lowbit(i)) {for (int j = col; j > 0; j -= lowbit(j)) {res += a[i][j];}}return res;}public int sumRegion(int row1, int col1, int row2, int col2) {row1++;row2++;col1++;col2++;return sum(row2, col2) - sum(row2, col1 - 1) - sum(row1 - 1, col2) + sum(row1 - 1, col1 - 1);}}/*** Your NumMatrix object will be instantiated and called as such:* NumMatrix obj = new NumMatrix(matrix);* obj.update(row,col,val);* int param_2 = obj.sumRegion(row1,col1,row2,col2);*/

