image.png
新年第一场，还行，AK了，虽然有点波折

5984. 拆分数位后四位数字的最小和

给你一个四位 正 整数 num 。请你使用 num 中的 数位 ，将 num 拆成两个新的整数 new1 和 new2 。new1 和 new2 中可以有 前导 0 ，且 num 中 所有 数位都必须使用。

  • 比方说，给你 num = 2932 ，你拥有的数位包括：两个 2 ，一个 9 和一个 3 。一些可能的 [new1, new2] 数对为 [22, 93]，[23, 92]，[223, 9] 和 [2, 329] 。

请你返回可以得到的 new1 和 new2 的 最小 和。

示例 1：
输入：num = 2932 输出：52 解释：可行的 [new1, new2] 数对为 [29, 23] ，[223, 9] 等等。 最小和为数对 [29, 23] 的和：29 + 23 = 52 。
示例 2：
输入：num = 4009 输出：13 解释：可行的 [new1, new2] 数对为 [0, 49] ，[490, 0] 等等。 最小和为数对 [4, 9] 的和：4 + 9 = 13 。

提示：

  • 1000 <= num <= 9999

思路：
拆出每一位，排个序
选前两个最小的数为两个数的十位，后两个较大的数为两个数的个位即可

  1. class Solution {
  2.     public int minimumSum(int num) {
  3.         int[] a = new int[4];
  5.         for (int i = 0; i < 4; i++) {
  6.             a[i] = num % 10;
  7.             num /= 10;
  8.         }
  10.         Arrays.sort(a);
  12.         return a[0] * 10 + a[2] + a[1] * 10 + a[3];
  14.     }
  15. }

5985. 根据给定数字划分数组

给你一个下标从 0 开始的整数数组 nums 和一个整数 pivot 。请你将 nums 重新排列，使得以下条件均成立：

  • 所有小于 pivot 的元素都出现在所有大于 pivot 的元素 之前 。
  • 所有等于 pivot 的元素都出现在小于和大于 pivot 的元素 中间 。
  • 小于 pivot 的元素之间和大于 pivot 的元素之间的 相对顺序 不发生改变。
    • 更正式的，考虑每一对 pi，pj ，pi 是初始时位置 i 元素的新位置，pj 是初始时位置 j 元素的新位置。对于小于 pivot 的元素，如果 i < j 且 nums[i] < pivot 和 nums[j] < pivot 都成立，那么 pi < pj 也成立。类似的，对于大于 pivot 的元素，如果 i < j 且 nums[i] > pivot 和 nums[j] > pivot 都成立，那么 pi < pj 。

请你返回重新排列 nums 数组后的结果数组。

示例 1：
输入：nums = [9,12,5,10,14,3,10], pivot = 10 输出：[9,5,3,10,10,12,14] 解释： 元素 9 ，5 和 3 小于 pivot ，所以它们在数组的最左边。 元素 12 和 14 大于 pivot ，所以它们在数组的最右边。 小于 pivot 的元素的相对位置和大于 pivot 的元素的相对位置分别为 [9, 5, 3] 和 [12, 14] ，它们在结果数组中的相对顺序需要保留。
示例 2：
输入：nums = [-3,4,3,2], pivot = 2 输出：[-3,2,4,3] 解释： 元素 -3 小于 pivot ，所以在数组的最左边。 元素 4 和 3 大于 pivot ，所以它们在数组的最右边。 小于 pivot 的元素的相对位置和大于 pivot 的元素的相对位置分别为 [-3] 和 [4, 3] ，它们在结果数组中的相对顺序需要保留。

提示：

  • 1 <= nums.length <= 105
  • -106 <= nums[i] <= 106
  • pivot 等于 nums 中的一个元素。

思路：
根据题意找出对应数字排序后再组合即可

  1. class Solution {
  2.     public int[] pivotArray(int[] nums, int p) {
  3.         List<Integer> l1 = new ArrayList<>();
  4.         List<Integer> l2 = new ArrayList<>();
  5.         int cnt = 0;
  6.         for (int x : nums) {
  7.             if (x < p)
  8.                 l1.add(x);
  9.             else if (x == p)
  10.                 cnt++;
  11.             else
  12.                 l2.add(x);
  13.         }
  14.         while (cnt-- > 0)
  15.             l1.add(p);
  16.         l1.addAll(l2);
  17.         int[] res = new int[nums.length];
  18.         for (int i = 0; i < nums.length; i++)
  19.             res[i] = l1.get(i);
  20.         return res;
  21.     }
  22. }

5986. 设置时间的最少代价

常见的微波炉可以设置加热时间，且加热时间满足以下条件：

  • 至少为 1 秒钟。
  • 至多为 99 分 99 秒。

你可以 最多 输入 4 个数字 来设置加热时间。如果你输入的位数不足 4 位，微波炉会自动加 前缀 0 来补足 4 位。微波炉会将设置好的四位数中，前 两位当作分钟数，后 两位当作秒数。它们所表示的总时间就是加热时间。比方说：

  • 你输入 9 5 4 （三个数字），被自动补足为 0954 ，并表示 9 分 54 秒。
  • 你输入 0 0 0 8 （四个数字），表示 0 分 8 秒。
  • 你输入 8 0 9 0 ，表示 80 分 90 秒。
  • 你输入 8 1 3 0 ，表示 81 分 30 秒。

给你整数 startAt ，moveCost ，pushCost 和 targetSeconds 。一开始，你的手指在数字 startAt 处。将手指移到 任何其他数字 ，需要花费 moveCost 的单位代价。每 输入你手指所在位置的数字一次，需要花费 pushCost 的单位代价。
要设置 targetSeconds 秒的加热时间，可能会有多种设置方法。你想要知道这些方法中，总代价最小为多少。
请你能返回设置 targetSeconds 秒钟加热时间需要花费的最少代价。
请记住，虽然微波炉的秒数最多可以设置到 99 秒，但一分钟等于 60 秒。

示例 1：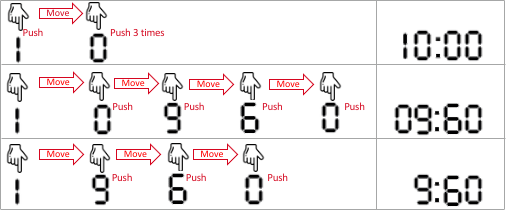
image.png
输入：startAt = 1, moveCost = 2, pushCost = 1, targetSeconds = 600 输出：6 解释：以下为设置加热时间的所有方法。 - 1 0 0 0 ，表示 10 分 0 秒。 手指一开始就在数字 1 处，输入 1 （代价为 1），移到 0 处（代价为 2），输入 0（代价为 1），输入 0（代价为 1），输入 0（代价为 1）。 总代价为：1 + 2 + 1 + 1 + 1 = 6 。这是所有方案中的最小代价。 - 0 9 6 0，表示 9 分 60 秒。它也表示 600 秒。 手指移到 0 处（代价为 2），输入 0 （代价为 1），移到 9 处（代价为 2），输入 9（代价为 1），移到 6 处（代价为 2），输入 6（代价为 1），移到 0 处（代价为 2），输入 0（代价为 1）。 总代价为：2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 = 12 。 - 9 6 0，微波炉自动补全为 0960 ，表示 9 分 60 秒。 手指移到 9 处（代价为 2），输入 9 （代价为 1），移到 6 处（代价为 2），输入 6（代价为 1），移到 0 处（代价为 2），输入 0（代价为 1）。 总代价为：2 + 1 + 2 + 1 + 2 + 1 = 9 。
示例 2：
image.png
输入：startAt = 0, moveCost = 1, pushCost = 2, targetSeconds = 76 输出：6 解释：最优方案为输入两个数字 7 6，表示 76 秒。 手指移到 7 处（代价为 1），输入 7 （代价为 2），移到 6 处（代价为 1），输入 6（代价为 2）。总代价为：1 + 2 + 1 + 2 = 6 其他可行方案为 0076 ，076 ，0116 和 116 ，但是它们的代价都比 6 大。

提示：

  • 0 <= startAt <= 9
  • 1 <= moveCost, pushCost <= 105
  • 1 <= targetSeconds <= 6039

思路：
这个题倒没多难，只有两种情况，分类讨论即可 :::danger 注意上界，会导致分钟数为100，不合法 :::

  1. class Solution {
  2.     public int minCostSetTime(int s, int mc, int pc, int ts) {
  3.         int x1 = ts / 60, y1 = ts % 60;
  4.         int min = Integer.MAX_VALUE;
  5.         int[] a = new int[4];
  6.         a[0] = x1 / 10;
  7.         a[1] = x1 % 10;
  8.         a[2] = y1 / 10;
  9.         a[3] = y1 % 10;
  11.         int sum = 0;
  12.         int pre = s;
  13.         int c0 = 0;
  14.         for (int i = 0; i < 4; i++) {
  15.             if (a[i] == 0 && c0 == i) {
  16.                 c0++;
  17.                 continue;
  18.             }
  19.             if (a[i] == pre) {
  20.                 sum += pc;
  21.             } else {
  22.                 sum += pc + mc;
  23.                 pre = a[i];
  24.             }
  25.         }
  26.         if (x1 != 100)
  27.             min = Math.min(min, sum);
  29.         if (y1 <= 39 && x1 > 0) {
  30.             x1--;
  31.             y1 += 60;
  32.             a[0] = x1 / 10;
  33.             a[1] = x1 % 10;
  34.             a[2] = y1 / 10;
  35.             a[3] = y1 % 10;
  36.             sum = 0; pre = s; c0 = 0;
  37.             for (int i = 0; i < 4; i++) {
  38.                 if (a[i] == 0 && c0 == i) {
  39.                     c0++;
  40.                     continue;
  41.                 }
  42.                 if (a[i] == pre) {
  43.                     sum += pc;
  44.                 } else {
  45.                     sum += pc + mc;
  46.                     pre = a[i];
  47.                 }
  48.             }
  49.             min = Math.min(min, sum);
  50.         }
  52.         return min;
  53.     }
  54. }

5987. 删除元素后和的最小差值

给你一个下标从 0 开始的整数数组 nums ，它包含 3 n 个元素。
你可以从 nums 中删除 恰好 n 个元素，剩下的 2 n 个元素将会被分成两个 相同大小 的部分。

  • 前面 n 个元素属于第一部分，它们的和记为 sumfirst 。
  • 后面 n 个元素属于第二部分，它们的和记为 sumsecond 。

两部分和的 差值 记为 sumfirst - sumsecond 。

  • 比方说，sumfirst = 3 且 sumsecond = 2 ，它们的差值为 1 。
  • 再比方，sumfirst = 2 且 sumsecond = 3 ，它们的差值为 -1 。

请你返回删除 n 个元素之后，剩下两部分和的 差值的最小值 是多少。

示例 1：
输入：nums = [3,1,2] 输出：-1 解释：nums 有 3 个元素，所以 n = 1 。 所以我们需要从 nums 中删除 1 个元素，并将剩下的元素分成两部分。 - 如果我们删除 nums[0] = 3 ，数组变为 [1,2] 。两部分和的差值为 1 - 2 = -1 。 - 如果我们删除 nums[1] = 1 ，数组变为 [3,2] 。两部分和的差值为 3 - 2 = 1 。 - 如果我们删除 nums[2] = 2 ，数组变为 [3,1] 。两部分和的差值为 3 - 1 = 2 。 两部分和的最小差值为 min(-1,1,2) = -1 。
示例 2：
输入：nums = [7,9,5,8,1,3] 输出：1 解释：n = 2 。所以我们需要删除 2 个元素，并将剩下元素分为 2 部分。 如果我们删除元素 nums[2] = 5 和 nums[3] = 8 ，剩下元素为 [7,9,1,3] 。和的差值为 (7+9) - (1+3) = 12 。 为了得到最小差值，我们应该删除 nums[1] = 9 和 nums[4] = 1 ，剩下的元素为 [7,5,8,3] 。和的差值为 (7+5) - (8+3) = 1 。 观察可知，最优答案为 1 。

提示：

  • nums.length == 3 * n
  • 1 <= n <= 105
  • 1 <= nums[i] <= 105

思路：
贪心 + 枚举 + 堆
枚举每个位置作为左边和右边的分界，从左边选n个最小的数，右边选n个最大的数相减，跟新全局最小值
找最小或最大的n个数可以用堆实现

  1. class Solution {
  2.     public long minimumDifference(int[] nums) {
  3.         int m = nums.length, n = m / 3;
  4.         PriorityQueue<Integer> q1 = new PriorityQueue<>();
  5.         long[] last = new long[m];
  7.         long s = 0;
  8.         for (int i = m - 1; i >= m - n; i--) {
  9.             s += nums[i];
  10.             q1.offer(nums[i]);
  11.         }
  12.         last[m - n] = s;
  13.         for (int i = m - n - 1; i >= 0; i--) {
  14.             if (nums[i] > q1.peek()) {
  15.                 int x = q1.poll();
  16.                 q1.offer(nums[i]);
  17.                 s = s - x + nums[i];
  18.             }
  19.             last[i] = s;
  20.         }
  22.         // System.out.println(Arrays.toString(last));
  24.         long sum = 0;
  25.         PriorityQueue<Integer> q = new PriorityQueue<>((o1, o2) -> (o2 - o1));
  26.         for (int i = 0; i < n; i++) {
  27.             sum += nums[i];
  28.             q.offer(nums[i]); 
  29.         }
  31.         long res = sum - last[n];
  32.         for (int i = n; i < 2 * n; i++) {
  33.             if (nums[i] < q.peek()) {
  34.                 int x = q.poll();
  35.                 q.offer(nums[i]);
  36.                 sum = sum - x + nums[i];
  37.             }
  38.             // System.out.println(sum + " " + last[i + 1]);
  39.             res = Math.min(res, sum - last[i + 1]);
  40.         }
  41.         return res;
  42.     }
  43. }