周赛 - 🏆 第 292 场力扣周赛 - 《学习笔记》

6056. 字符串中最大的 3 位相同数字
6057. 统计值等于子树平均值的节点数
6058. 统计打字方案数
6059. 检查是否有合法括号字符串路径

无wrong，国际服崩了，不知道还算不算分

6056. 字符串中最大的 3 位相同数字

给你一个字符串 num ，表示一个大整数。如果一个整数满足下述所有条件，则认为该整数是一个 优质整数 ：

该整数是 num 的一个长度为 3 的 子字符串 。
该整数由唯一一个数字重复 3 次组成。

以字符串形式返回 最大的优质整数 。如果不存在满足要求的整数，则返回一个空字符串 “” 。
注意：

子字符串 是字符串中的一个连续字符序列。
num 或优质整数中可能存在 前导零 。

示例 1：
输入：num = “6777_133339” 输出：“777” 解释：num 中存在两个优质整数：”777” 和 “333” 。 “777” 是最大的那个，所以返回 “777” 。
示例 2：
输入：num = “23000_19” 输出：“000” 解释：“000” 是唯一一个优质整数。
示例 3：
输入：num = “42352338” 输出：“” 解释：不存在长度为 3 且仅由一个唯一数字组成的整数。因此，不存在优质整数。

提示：

3 <= num.length <= 1000
num 仅由数字（0 - 9）组成

思路：
从9到0看哪个三位数出现了，都没有返回空串
时间复杂度：O(10n)

class Solution {
    public String largestGoodInteger(String s) {
        int n = s.length();
        for (char c = '9'; c >= '0'; c--) {
            String t = c + "" + c + "" + c;
            for (int i = 0; i + 3 <= n; i++) {
                if (t.equals(s.substring(i, i + 3))) {
                    return t;
                }
            }
        }
        return "";
    }
}

6057. 统计值等于子树平均值的节点数

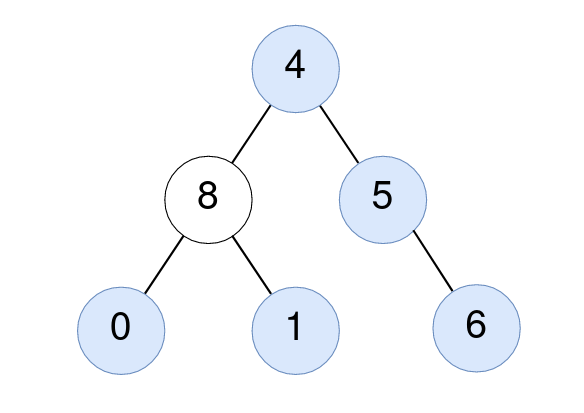
给你一棵二叉树的根节点 root ，找出并返回满足要求的节点数，要求节点的值等于其子树中值的 平均值 。
注意：

n 个元素的平均值可以由 n 个元素求和然后再除以 n ，并 向下舍入 到最近的整数。
root 的子树由 root 和它的所有后代组成。

示例 1：
输入：root = [4,8,5,0,1,null,6] 输出：5 解释： 对值为 4 的节点：子树的平均值 (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4 。对值为 5 的节点：子树的平均值 (5 + 6) / 2 = 11 / 2 = 5 。对值为 0 的节点：子树的平均值 0 / 1 = 0 。对值为 1 的节点：子树的平均值 1 / 1 = 1 。对值为 6 的节点：子树的平均值 6 / 1 = 6 。
示例 2：
输入：root = [1] 输出：1 解释：对值为 1 的节点：子树的平均值 1 / 1 = 1。

提示：

树中节点数目在范围 [1, 1000] 内
0 <= Node.val <= 1000

思路：
后续遍历，计算每个子树的平均值
时间复杂度：O(n)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int cnt = 0;
    public int averageOfSubtree(TreeNode root) {
        dfs(root);
        return cnt;
    }
    int[] dfs(TreeNode root) {
        if (root == null)
            return new int[]{0, 0};
        int[] l = dfs(root.left);
        int[] r = dfs(root.right);
        int sum = l[0] + r[0] + root.val, c = l[1] + r[1] + 1;
        if (sum / c == root.val)
            cnt++;
        return new int[]{sum, c};
    }
}

6058. 统计打字方案数

Alice 在给 Bob 用手机打字。数字到字母的对应如下图所示。

为了打出一个字母，Alice 需要按对应字母 i 次，i 是该字母在这个按键上所处的位置。

比方说，为了按出字母 ‘s’ ，Alice 需要按 ‘7’ 四次。类似的， Alice 需要按 ‘5’ 两次得到字母 ‘k’ 。
注意，数字 ‘0’ 和 ‘1’ 不映射到任何字母，所以 Alice 不使用它们。

但是，由于传输的错误，Bob 没有收到 Alice 打字的字母信息，反而收到了 按键的字符串信息 。

比方说，Alice 发出的信息为 “bob” ，Bob 将收到字符串 “2266622” 。

给你一个字符串 pressedKeys ，表示 Bob 收到的字符串，请你返回 Alice 总共可能发出多少种文字信息 。
由于答案可能很大，将它对 109 + 7 取余后返回。

示例 1：
输入：pressedKeys = “22233” 输出：8 解释： Alice 可能发出的文字信息包括： “aaadd”, “abdd”, “badd”, “cdd”, “aaae”, “abe”, “bae” 和 “ce” 。由于总共有 8 种可能的信息，所以我们返回 8 。
示例 2：
输入：pressedKeys = “222222222222222222222222222222222222” 输出：82876089 解释： 总共有 2082876103 种 Alice 可能发出的文字信息。由于我们需要将答案对 109 + 7 取余，所以我们返回 2082876103 % (109 + 7) = 82876089 。

提示：

1 <= pressedKeys.length <= 105
pressedKeys 只包含数字 ‘2’ 到 ‘9’ 。

思路：
线性DP
状态表示：f[i]表示前i个按键能发出的总信息数
初始化: f[0] = 1
状态转移：
考虑最后一个字母按了几次最多3或4个连续相同的字母
f[i] = (f[i] + f[j - 1]) % mod

class Solution {
    public int countTexts(String s) {
        int[] max = {0, 0, 3, 3, 3, 3, 3, 4, 3, 4};
        int n = s.length();
        int[] f = new int[n + 1];
        int mod = (int)(1e9 + 7);
        f[0] = 1;
        for (int i = 1; i <= n; i++) {
            int x = s.charAt(i - 1) - '0';
            for (int j = i; j > Math.max(0, i - max[x]); j--) {
                int y = s.charAt(j - 1) - '0';
                if (x != y) break;
                else
                    f[i] = (f[i] + f[j - 1]) % mod;
            }
        }
        return f[n];
    }
}

6059. 检查是否有合法括号字符串路径

一个括号字符串是一个非空且只包含 ‘(‘ 和 ‘)’ 的字符串。如果下面任意条件为真，那么这个括号字符串就是 合法的 。

字符串是 () 。
字符串可以表示为 AB（A 连接 B），A 和 B 都是合法括号序列。
字符串可以表示为 (A) ，其中 A 是合法括号序列。

给你一个 m x n 的括号网格图矩阵 grid 。网格图中一个 合法括号路径 是满足以下所有条件的一条路径：

路径开始于左上角格子 (0, 0) 。
路径结束于右下角格子 (m - 1, n - 1) 。
路径每次只会向下或者向右移动。
路径经过的格子组成的括号字符串是合法的。

如果网格图中存在一条 合法括号路径 ，请返回 true ，否则返回 false 。

示例 1：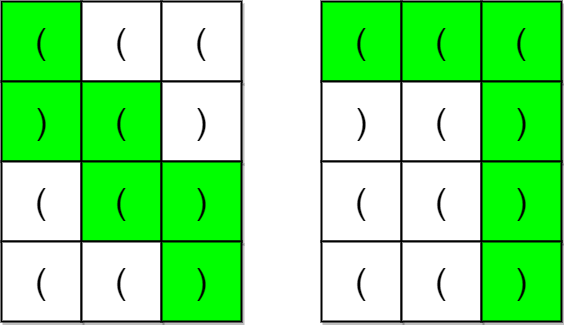

输入：grid = [[“(“,”(“,”(“],[“)”,”(“,”)”],[“(“,”(“,”)”],[“(“,”(“,”)”]] 输出：true 解释：上图展示了两条路径，它们都是合法括号字符串路径。第一条路径得到的合法字符串是 “()(())” 。第二条路径得到的合法字符串是 “((()))” 。注意可能有其他的合法括号字符串路径。
示例 2：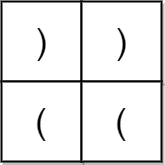

输入：grid = [[“)”,”)”],[“(“,”(“]] 输出：false 解释：两条可行路径分别得到 “))(“ 和 “)((“ 。由于它们都不是合法括号字符串，我们返回 false 。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 100
grid[i][j] 要么是 ‘(‘ ，要么是 ‘)’

思路：
DP
f[i][j][k]表示位于i, j坐标时左括号个数为k个是否出现
初始化: f[0][0][1] = true
状态转移：
f[i][j][k] = f[i][j - 1][k - c[i][j] = '(' ? 1 : -1]
f[i][j][k] = f[i - 1][j][k - c[i][j] = '(' ? 1 : -1]
当然k < 0全部都是非法状态

class Solution {
    public boolean hasValidPath(char[][] c) {
        int n = c.length, m = c[0].length;
        if ((n + m - 1) % 2 != 0 || c[0][0] == ')' || c[n - 1][m - 1] == '(')
            return false;
        boolean[][][] f = new boolean[n][m][n + m];
        f[0][0][1] = true;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (i > 0 || j > 0) {
                    int t = c[i][j] == '(' ? 1 : -1;
                    for (int k = 0; k < n + m; k++) {
                        int x = k - t;
                        if (x >= 0 && x < n + m) {
                            if (i - 1 >= 0) f[i][j][k] = f[i][j][k] || f[i - 1][j][x];
                            if (j - 1 >= 0) f[i][j][k] = f[i][j][k] || f[i][j - 1][x];
                        }
                    }
                }
            }
        }
        return f[n - 1][m - 1][0];
    }
}