分割数组

410. 分割数组的最大值

给定一个非负整数数组 nums 和一个整数 m ，你需要将这个数组分成 m 个非空的连续子数组。
设计一个算法使得这 m 个子数组各自和的最大值最小。

示例 1：
输入：nums = [7,2,5,10,8], m = 2 输出：18 解释： 一共有四种方法将 nums 分割为 2 个子数组。 其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。 因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。
示例 2：
输入：nums = [1,2,3,4,5], m = 2 输出：9
示例 3：
输入：nums = [1,4,4], m = 3 输出：4

提示：

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 106
• 1 <= m <= min(50, nums.length)

思路：
方法1：由于结果具有二分性，可以二分答案找到子数组最大和的最小值
时间复杂度：O(NlogN)
方法2：DP，分割类型的DP
状态表示：f[i][j]意思是前i个元素分成j组的所有分法。
属性：最大的子数组的和
状态转移：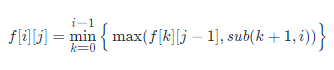

初始化：全部初始化为一个极大值，0个元素的所有分组f[0][j]置为0。
再用一个前缀和辅助计算！！
时间复杂度：O(N2M)

// 二分
class Solution {
    public int splitArray(int[] nums, int m) {
        int sum = Arrays.stream(nums).sum();
        int max = 0;
        for (int x : nums)
            max = Math.max(x, max);
        int l = Math.max(sum / m, max), r = sum;
        while (l < r) {
            int mid = l + (r - l >> 1);
            if (check(nums, mid, m)) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        return l;
    }
    boolean check(int[] nums, int up, int m) {
        int cnt = 0;
        int sum = 0;
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
            if (sum > up) {
                cnt++;
                sum = nums[i];
            }
        }
        return cnt + 1 <= m;
    }
}

//DP
class Solution {
    public int splitArray(int[] nums, int m) {
        int n = nums.length;
        int[][] f = new int[n + 1][m + 1];
        for (int i = 1; i <= n; i++)
            Arrays.fill(f[i], (int)(2e9));
        int[] pre = new int[n + 1];
        for (int i = 1; i <= n; i++)
            pre[i] = pre[i - 1] + nums[i - 1];
        for (int i = 1; i <= n; i++) {
            f[i][1] = pre[i];
            for (int j = 2; j <= m; j++) {
                for (int k = 1; k < i; k++) {
                    f[i][j] = Math.min(f[i][j], Math.max(f[k][j - 1], pre[i] - pre[k]));
                }
            }
        }
        return f[n][m];
    }
}