动态规划DP - 区间DP - 《学习笔记》

282. 石子合并">282. 石子合并
POJ - 1141 Brackets Sequence">POJ - 1141 Brackets Sequence
参考文档

区间DP的状态设计相对简单，基本大部分问题都是用 f[i][j] 代表区间 [i, j] 的最优解。难点在于状态转移的设计上。

涉及到利用区间DP 来求解的问题，一般都有一个对应的序列：

1）当序列的长度为 n <= 300 时，区间DP 的时间复杂度一般为 O(n^3) ，其中状态转移时间复杂度 O(n)
2）当序列的长度为 n <= 1000 时，区间DP 的时间复杂度一般为 O(n^2) ，其中状态转移时间复杂度 O(1)

注意：

永远不去想第一步要干什么，而是想最后一步是要干什么，然后再去枚举最后一步的所有情况，从而缩小区间。
有时候二维的区间无法表示状态，或者无法进行状态转移的时候，我们可以尝试再增加一个纬度，然后再去想状态转移方程。

282. 石子合并

题目描述
设有N堆石子排成一排，其编号为1，2，3，…，N。

每堆石子有一定的质量，可以用一个整数来描述，现在要将这N堆石子合并成为一堆。

每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同。

例如有4堆石子分别为 1 3 5 2，我们可以先合并1、2堆，代价为4，得到4 5 2，又合并 1，2堆，代价为9，得到9 2 ，再合并得到11，总代价为4+9+11=24；

如果第二步是先合并2，3堆，则代价为7，得到4 7，最后一次合并代价为11，总代价为4+7+11=22。

问题是：找出一种合理的方法，使总的代价最小，输出最小代价。

输入格式：
第一行一个数 N 表示石子的堆数 N。
第二行 N 个数，表示每堆石子的质量(均不超过 1000)。
输出格式：
输出一个整数，表示最小代价。
数据范围：
1≤N≤300
输入样例

4
1 3 5 2

输出样例

方法1：穷举
时间复杂度： O(n!)

区间DP - 图1
可以从图中看出有好多重复计算。

方法2：区间 DP
深搜时所有叶节点都是一样的，是整个数组的前缀和！
故假设已经合并了 n - 2 堆，只剩最后一堆待合并。
假设最后一次合并发生在位置 k ，有 f[1][n] = f[1][k] + f[k + 1][n]
问题变为求最小的 f[1][k] 和 f[k + 1][n]
通过这种方法直至将区间规模缩小为1，就能得到整个问题的解了！

状态表示： f[i][j]表示从第 i 堆石子到第 j 堆石子合并成一堆所花费的最小代价。
状态转移：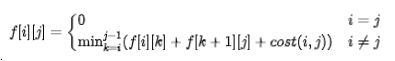
其中cost(i, j)为合并 i, j 的花费
1） i == j 已经是一堆，不需要合并
2） i != j 把目前剩下的两堆合并，一堆是 f[i][k] ，另一堆是 f[k + 1][j] ，这两堆合并的消耗就是从 i 到 j 堆的重量之和。对于合并方案，总共有 k = j - i 种选择，所以枚举 j - i 次取其中最小值就是答案了。
代码可以通过记忆化搜索或者递推的方式来写！！！

改图表示了迭代求解的顺序，假设初始时有5堆石子。灰色格子要么是无效状态，要么是不需要求解的状态。红色的格子代表为长度为 2 的区间，橙色的格子代表为长度为 3 的区间，金黄色的格子则代表长度为 4 的区间，黄色的格子代表我们最终要求的区间状态，即 f[1][5] 。
区间DP - 图3

时间复杂度：
每段区间和都枚举：O(n^3)
用前缀和代替区间和枚举： O(n^2)

import java.util.*;
public class Main {
    static int[] a;
    static int[][] f;
    public static void main(String ... args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        a = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            a[i] = sc.nextInt();
            a[i] += a[i - 1];   //求前缀和
        }
        f = new int[n + 1][n + 1];
        for (int i = 0; i <= n; i++)
            Arrays.fill(f[i], 0x3f3f3f3f);
        System.out.println(dp(1, n));
    }
    static int dp(int i, int j) {
        if (f[i][j] != 0x3f3f3f3f)
            return f[i][j];
        if (i == j)
            return 0;
        int res = 0x3f3f3f3f;
        for (int k = i; k < j; k++) {
            res = Math.min(res, dp(i, k) + dp(k + 1, j) + a[j] - a[i - 1]);
        }
        return f[i][j] = res;
    }
}

// 递推
import java.util.*;
public class Main {
    public static void main(String ... args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] a = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            a[i] = sc.nextInt();
            a[i] += a[i - 1];   //求前缀和
        }
        int[][] f = new int[n + 1][n + 1];
        for (int len = 2; len <= n; len++) {
            for (int i = 1; i + len - 1 <= n; i++) {
                int j = i + len - 1;
                f[i][j] = 0x3f3f3f3f;
                int sum = a[j] - a[i - 1];
                for (int k = i; k < j; k++)
                    f[i][j] = Math.min(f[i][j], f[i][k] + f[k + 1][j] + sum);
            }
        }
        System.out.println(f[1][n]);
    }
}

POJ - 1141 Brackets Sequence

用以下方式定义合法的括号字符串

1.空串是合法的
2. 如果S是合法的, 那么(S)和[S]也都是合法的
3. 如果A和B是合法的, 那么AB是一个合法的字符串.

举个栗子, 下列字符串都是合法的括号字符串:
(), [], (()), ([]), ()[], ()[()]

下面这些不是:
(, [, ), )(, ([)], ([(]

给出一个由字符’(‘, ‘)’, ‘[‘, 和’]’构成的字符串. 你的任务是找出一个最短的合法字符串，使得给出的字符串是这个字符串的子序列。对于字符串a1 a2 ... an, b1 b2 ... bm 当且仅当对于1 ≤ i1 < i2 < ... < in ≤ m, 使得对于所有1 ≤ j ≤ n，aj = bij时, aj是bi的子序列

输入一个只含有’(‘, ‘)’, ‘[‘, ‘]’字符的字符串，字符串的最大长度是100

输出一个最短的合法字符串，使得输入的字符串是输出字符串的子序列（可能有多种情况，任意一种情况都可以）

样例：
([(]
()[()]

思路：
想一下最后一步是什么，选择一个 k，范围是1 <= k < n ，最终的结果是 f[1, n] = min(f[1, k] + f[k + 1, n] k = 1, 2, ..., n。
由此可以想到本题可以使用区间DP的方法

状态表示： f[i][j] 表示从i到j的字符串变成合法字符串至少要增加的字符个数。
状态转移：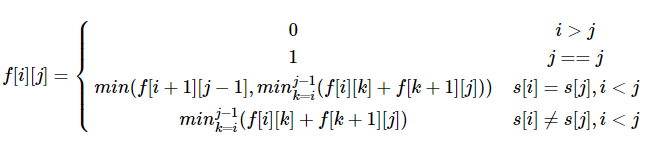

f[i][j] = \left\{\begin{matrix} 0 & i > j \\ 1 & j == j\\ min(f[i + 1][j - 1], min_{k = i}^{j - 1}(f[i][k] + f[k + 1][j])) & s[i] = s[j] , i < j\\ min_{k = i}^{j - 1}(f[i][k] + f[k + 1][j]) & s[i] \neq s[j], i < j \end{matrix}\right.

本题的最终目标不是问将源字符串变为合法字符串需要几个字符，而是问最终的目标字符串是什么。
所以需要根据最终的 f[1][n] 一步步向前推导出整个字符串，具体见代码。

// 记忆化搜索
import java.util.*;
public class Main {
    static final int INF = (int)(1e9);
    static String s;
    static int[][] f;
    static int n;
    public static void main(String ... args){
        Scanner sc = new Scanner(System.in);
        s = sc.nextLine();
        n = s.length();
        f = new int[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(f[i], INF);
        }
        dp(0, n - 1);
//         for (int i = 0; i < n; i++)
//             System.out.println(Arrays.toString(f[i]));
        print(0, n - 1);
         System.out.println();
    }
    static int dp(int i, int j) {
        if (i > j) return j >= 0 ? f[i][j] = 0 : 0;
        if (i == j) return f[i][j] = 1;
        if (f[i][j] != INF)
            return f[i][j];
        int res = INF;
        if (match(i, j))
            res = dp(i + 1, j - 1);
        for (int k = i; k < j; k++)
            res = Math.min(res, dp(i, k) + dp(k + 1, j));
        return f[i][j] = res;
    }
    static void print(int i, int j) {
        if (i > j) return;
        if (i == j) {
            if (s.charAt(i) == '(' || s.charAt(i) == ')')
                System.out.print("()");
            else
                System.out.print("[]");
            return;
        }
        if (match(i, j) && f[i][j] == f[i + 1][j - 1]) {
            System.out.print(s.charAt(i));
            print(i + 1, j - 1);
            System.out.print(s.charAt(j));
            return;
        }
        for (int k = i; k < j; k++) {
            if (f[i][j] == f[i][k] + f[k + 1][j]) {
                print(i, k);
                print(k + 1, j);
                return;
            }
        }
    }
    static boolean match(int i, int j) {
        return (s.charAt(i) == '(' && s.charAt(j) == ')') || (s.charAt(i) == '[' && s.charAt(j) == ']');
    }
}

//迭代法
import java.util.*;
public class Main {
    static String s;
    static int n;
    static int[][] f;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        s = sc.nextLine();
        n = s.length();
        f = new int[n + 1][n + 1];
        s = " " + s;
        for (int len = 1; len <= n; len++) {
            for (int i = 1; i + len - 1 <= n; i++) {
                int j = i + len - 1;
                if (i == j) f[i][j] = 1;
                else {
                    f[i][j] = 0x3f3f3f3f;
                    if (match(i, j)) f[i][j] = f[i + 1][j - 1];
                    for (int k = i; k < j; k++)
                        f[i][j] = Math.min(f[i][j], f[i][k] + f[k + 1][j]);
                }
            }
        }
        print(1, n);
        System.out.println();
    }
    static void print(int i, int j) {
        if (i > j) return;
        if (i == j) {
            if (s.charAt(i) == '(' || s.charAt(i) == ')')
                System.out.print("()");
            else System.out.print("[]");
            return;
        }
        if (match(i, j) && f[i][j] == f[i + 1][j - 1]) {
            System.out.print(s.charAt(i));
            print(i + 1, j - 1);
            System.out.print(s.charAt(j));
            return;
        }
        for (int k = i; k < j; k++) {
            if (f[i][j] == f[i][k] + f[k + 1][j]) {
                print(i, k);
                print(k + 1, j);
                return;
            }
        }
    }
    static boolean match(int i, int j) {
        return s.charAt(i) == '(' && s.charAt(j) ==')' || s.charAt(i) == '[' && s.charAt(j) == ']';
    }
}

参考文档

夜深人静写算法（二十七）- 区间DP