拉了拉了,第二题做的我心态爆照,注意到了long,却忘记一个初始化。
t3一次wrong是因为少考虑了一种情况
t4是因为没考虑相同时间的情况,第二次wrong是因为dijkstra条件判断没写对
5938. 找出数组排序后的目标下标
给你一个下标从 0 开始的整数数组 nums 以及一个目标元素 target 。
目标下标 是一个满足 nums[i] == target 的下标 i 。
将 nums 按 非递减 顺序排序后,返回由 nums 中目标下标组成的列表。如果不存在目标下标,返回一个 空 列表。返回的列表必须按 递增 顺序排列。
示例 1:
输入:nums = [1,2,5,2,3], target = 2 输出:[1,2] 解释:排序后,nums 变为 [1,2,2,3,5] 。 满足 nums[i] == 2 的下标是 1 和 2 。
示例 2:
输入:nums = [1,2,5,2,3], target = 3 输出:[3] 解释:排序后,nums 变为 [1,2,2,3,5] 。 满足 nums[i] == 3 的下标是 3 。
示例 3:
输入:nums = [1,2,5,2,3], target = 5 输出:[4] 解释:排序后,nums 变为 [1,2,2,3,5] 。 满足 nums[i] == 5 的下标是 4 。
示例 4:
输入:nums = [1,2,5,2,3], target = 4 输出:[] 解释:nums 中不含值为 4 的元素。
提示:
- 1 <= nums.length <= 100
- 1 <= nums[i], target <= 100
思路:
排序 +遍历
class Solution {public List<Integer> targetIndices(int[] nums, int target) {Arrays.sort(nums);List<Integer> res = new ArrayList<>();for (int i = 0; i < nums.length; i++) {if (nums[i] == target)res.add(i);}return res;}}
5939. 半径为 k 的子数组平均值
给你一个下标从 0 开始的数组 nums ,数组中有 n 个整数,另给你一个整数 k 。
半径为 k 的子数组平均值 是指:nums 中一个以下标 i 为 中心 且 半径 为 k 的子数组中所有元素的平均值,即下标在 i - k 和 i + k 范围(含 i - k 和 i + k)内所有元素的平均值。如果在下标 i 前或后不足 k 个元素,那么 半径为 k 的子数组平均值 是 -1 。
构建并返回一个长度为 n 的数组 _avgs ,其中 avgs[i] _是以下标 i 为中心的子数组的 半径为 k 的子数组平均值 。
x 个元素的 平均值 是 x 个元素相加之和除以 x ,此时使用截断式 整数除法 ,即需要去掉结果的小数部分。
- 例如,四个元素 2、3、1 和 5 的平均值是 (2 + 3 + 1 + 5) / 4 = 11 / 4 = 3.75,截断后得到 3 。
示例 1: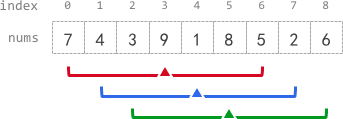
输入:nums = [7,4,3,9,1,8,5,2,6], k = 3 输出:[-1,-1,-1,5,4,4,-1,-1,-1] 解释: - avg[0]、avg[1] 和 avg[2] 是 -1 ,因为在这几个下标前的元素数量都不足 k 个。 - 中心为下标 3 且半径为 3 的子数组的元素总和是:7 + 4 + 3 + 9 + 1 + 8 + 5 = 37 。 使用截断式 整数除法,avg[3] = 37 / 7 = 5 。 - 中心为下标 4 的子数组,avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4 。 - 中心为下标 5 的子数组,avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4 。 - avg[6]、avg[7] 和 avg[8] 是 -1 ,因为在这几个下标后的元素数量都不足 k 个。
示例 2:
输入:nums = [100000], k = 0 输出:[100000] 解释: - 中心为下标 0 且半径 0 的子数组的元素总和是:100000 。 avg[0] = 100000 / 1 = 100000 。
示例 3:
输入:nums = [8], k = 100000 输出:[-1] 解释: - avg[0] 是 -1 ,因为在下标 0 前后的元素数量均不足 k 。
提示:
n == nums.length1 <= n <= 1050 <= nums[i], k <= 105
思路:
模拟即可,注意边界,注意初始化。
class Solution {public int[] getAverages(int[] nums, int k) {int n = nums.length;int[] res = new int[n];Arrays.fill(res, -1);long sum = 0;for (int i = 0; i < n; i++) {sum += nums[i];if (i >= 2 * k)res[i - k] = (int)(sum / (2 * k + 1));if (i >= 2 * k)sum -= nums[i - 2 * k];}return res;}}
5940. 从数组中移除最大值和最小值
给你一个下标从 0 开始的数组 nums ,数组由若干 互不相同 的整数组成。
nums 中有一个值最小的元素和一个值最大的元素。分别称为 最小值 和 最大值 。你的目标是从数组中移除这两个元素。
一次 删除 操作定义为从数组的 前面 移除一个元素或从数组的 后面 移除一个元素。
返回将数组中最小值和最大值 都 移除需要的最小删除次数。
示例 1:
输入:nums = [2,10,7,5,4,1,8,6] 输出:5 解释: 数组中的最小元素是 nums[5] ,值为 1 。 数组中的最大元素是 nums[1] ,值为 10 。 将最大值和最小值都移除需要从数组前面移除 2 个元素,从数组后面移除 3 个元素。 结果是 2 + 3 = 5 ,这是所有可能情况中的最小删除次数。
示例 2:
输入:nums = [0,-4,19,1,8,-2,-3,5] 输出:3 解释: 数组中的最小元素是 nums[1] ,值为 -4 。 数组中的最大元素是 nums[2] ,值为 19 。 将最大值和最小值都移除需要从数组前面移除 3 个元素。 结果是 3 ,这是所有可能情况中的最小删除次数。
示例 3:
输入:nums = [101] 输出:1 解释: 数组中只有这一个元素,那么它既是数组中的最小值又是数组中的最大值。 移除它只需要 1 次删除操作。
提示:
1 <= nums.length <= 105-105 <= nums[i] <= 105nums中的整数 互不相同
思路:
找到最小值和最大值对应的下标。
删除无非三种情况:
- 都从左边删
- 都从右边删
- 一个从左边,一个从右边删
class Solution {public int minimumDeletions(int[] nums) {int i1 = 0, i2 = 0;int max = -0x3f3f3f3f, min = 0x3f3f3f3f;int n = nums.length;for (int i = 0; i < n; i++) {if (nums[i] < min) {min = nums[i];i1 = i;}if (nums[i] > max) {max = nums[i];i2 = i;}}if (i1 > i2) {int t = i1;i1 = i2;i2 = t;}return Math.min(i2 + 1, Math.min(n - i1, n - (i2 - i1 - 1)));}}
5941. 找出知晓秘密的所有专家
给你一个整数 n ,表示有 n 个专家从 0 到 n - 1 编号。另外给你一个下标从 0 开始的二维整数数组 meetings ,其中 meetings[i] = [xi, yi, timei] 表示专家 xi 和专家 yi 在时间 timei 要开一场会。一个专家可以同时参加 多场会议 。最后,给你一个整数 firstPerson 。
专家 0 有一个 秘密 ,最初,他在时间 0 将这个秘密分享给了专家 firstPerson 。接着,这个秘密会在每次有知晓这个秘密的专家参加会议时进行传播。更正式的表达是,每次会议,如果专家 xi 在时间 timei 时知晓这个秘密,那么他将会与专家 yi 分享这个秘密,反之亦然。
秘密共享是 瞬时发生 的。也就是说,在同一时间,一个专家不光可以接收到秘密,还能在其他会议上与其他专家分享。
在所有会议都结束之后,返回所有知晓这个秘密的专家列表。你可以按 任何顺序 返回答案。
示例 1:
输入:n = 6, meetings = [[1,2,5],[2,3,8],[1,5,10]], firstPerson = 1 输出:[0,1,2,3,5] 解释: 时间 0 ,专家 0 将秘密与专家 1 共享。 时间 5 ,专家 1 将秘密与专家 2 共享。 时间 8 ,专家 2 将秘密与专家 3 共享。 时间 10 ,专家 1 将秘密与专家 5 共享。 因此,在所有会议结束后,专家 0、1、2、3 和 5 都将知晓这个秘密。
示例 2:
输入:n = 4, meetings = [[3,1,3],[1,2,2],[0,3,3]], firstPerson = 3 输出:[0,1,3] 解释: 时间 0 ,专家 0 将秘密与专家 3 共享。 时间 2 ,专家 1 与专家 2 都不知晓这个秘密。 时间 3 ,专家 3 将秘密与专家 0 和专家 1 共享。 因此,在所有会议结束后,专家 0、1 和 3 都将知晓这个秘密。
示例 3:
输入:n = 5, meetings = [[3,4,2],[1,2,1],[2,3,1]], firstPerson = 1 输出:[0,1,2,3,4] 解释: 时间 0 ,专家 0 将秘密与专家 1 共享。 时间 1 ,专家 1 将秘密与专家 2 共享,专家 2 将秘密与专家 3 共享。 注意,专家 2 可以在收到秘密的同一时间分享此秘密。 时间 2 ,专家 3 将秘密与专家 4 共享。 因此,在所有会议结束后,专家 0、1、2、3 和 4 都将知晓这个秘密。
示例 4:
输入:n = 6, meetings = [[0,2,1],[1,3,1],[4,5,1]], firstPerson = 1 输出:[0,1,2,3] 解释: 时间 0 ,专家 0 将秘密与专家 1 共享。 时间 1 ,专家 0 将秘密与专家 2 共享,专家 1 将秘密与专家 3 共享。 因此,在所有会议结束后,专家 0、1、2 和 3 都将知晓这个秘密。
提示:
2 <= n <= 1051 <= meetings.length`` <= 105meetings[i].length == 30 <= xi, yi <= n - 1xi != yi1 <= timei <= 1051 <= firstPerson <= n - 1
思路:
比赛时用的dijkstra。赛后发现好多种方法,记录一下。
方法1:dijkstra
建好稀疏图。使用堆优化版dijkstra,比较器是知道秘密的时间,小根堆。出队的元素一定是当前最早知道秘密的人。
如果该元素已经被更新过,跳过即可;否则用更新他能到的其它点(即与他开会的其它人),若会议时间小于等于该元素知道秘密的时间,更新答案,将对应节点入堆。
方法2:排序 + 正反两次遍历
对会议按照时间从小到大排序
正着遍历一遍记录每个人得知秘密(如果能的话)的最小时间。
反着再遍历一遍是因为可能有好几个会议时间一致,导致可能有人本该知道秘密却因为已经遍历过去而不知道。
反着遍历可确保能得知秘密的每个人都能得知秘密。
// dijkstraclass Solution {final int N = 200010, INF = 0x3f3f3f3f;int idx = 0;int[] h = new int[N], e = new int[N], w = new int[N], ne = new int[N];boolean[] st = new boolean[N];public List<Integer> findAllPeople(int n, int[][] ms, int firstPerson) {List<Integer> res = new ArrayList<>();PriorityQueue<int[]> q = new PriorityQueue<>((o1, o2) -> (o1[1] - o2[1]));Arrays.fill(h, -1);for (int[] p : ms) {int a = p[0], b = p[1], c = p[2];add(a, b, c);add(b, a, c);}q.offer(new int[]{0, 0});q.offer(new int[]{firstPerson, 0});while (!q.isEmpty()) {int[] p = q.poll();int x = p[0], y = p[1];if (st[x]) continue;st[x] = true;res.add(x);for (int i = h[x]; i != -1; i = ne[i]) {int j = e[i], t = w[i];if (t >= y) {q.offer(new int[]{j, t});}}}return res;}void add(int a, int b, int c) {e[idx] = b;w[idx] = c;ne[idx] = h[a];h[a] = idx++;}}
// 方法2:排序 + 正反遍历class Solution {final int INF = 0x3f3f3f3f;public List<Integer> findAllPeople(int n, int[][] ms, int firstPerson) {Arrays.sort(ms, (o1, o2) -> (o1[2] - o2[2]));int[] st = new int[n];Arrays.fill(st, INF);st[0] = st[firstPerson] = 0;for (int[] p : ms) {int a = p[0], b = p[1], c = p[2];if (st[a] != INF || st[b] != INF) {st[a] = Math.min(st[a], c);st[b] = Math.min(st[b], c);}}for (int i = ms.length - 1; i >= 0; i--) {int a = ms[i][0], b = ms[i][1], c = ms[i][2];if (st[a] != INF && st[b] != INF)continue;if (st[a] == INF && st[b] == INF)continue;if (st[a] != INF && st[a] <= c)st[b] = c;else if (st[b] != INF && st[b] <= c)st[a] = c;}List<Integer> res = new ArrayList<>();for (int i = 0; i < n; i++)if (st[i] != INF)res.add(i);return res;}}
写完后又相想了一下,发现不对,大问题二次遍历相同的时间如果有新的节点知道秘密,还得继续遍历相同时间直至没有新人知道秘密! 样例:5, [2, 3, 3], [1, 2, 3], [3, 4, 3], 4
方法3:并查集
按开会时间操作并查集
相同时间的一起处理,所以先将会议按时间从小到大排序
每个时间的所有会议遍历两次
- 第一次合并集合
- 第二次孤立集合,也就是说那些在本次时间接触不到秘密的节点会重新为与自己组成一个集合
这样遍历完后所有能接触到秘密的节点都会与0节点在同一集合!
class Solution {class UnionFind {int n;int[] fa;// int[] rank; // 按秩合并,如果需要的话可以加//int[] size; // 集合的大小,在根节点中维护,如果需要的话可以加//int setCnt; //连通块的数量,如果需要的话可以加UnionFind(int n) {this.n = n;fa = new int[n];for (int i = 0; i < n; i++)fa[i] = i;}int find(int x) {return x == fa[x] ? x : (fa[x] = find(fa[x]));}boolean isConnected(int x, int y) {int px = find(x), py = find(y);return px == py;}void union(int x, int y) {int px = find(x), py = find(y);fa[py] = px;}void isolate(int x) {fa[x] = x;}}public List<Integer> findAllPeople(int n, int[][] ms, int firstPerson) {Arrays.sort(ms, (o1, o2) -> o1[2] - o2[2]);UnionFind uf = new UnionFind(n);int m = ms.length;uf.union(0, firstPerson);for (int i = 0; i < m; i++) {int j = i;while (j + 1 < m && ms[j + 1][2] == ms[i][2])j++;for (int k = i; k <= j; k++)uf.union(ms[k][0], ms[k][1]);for (int k = i; k <= j; k++) {if (!uf.isConnected(ms[k][0], 0)) {uf.isolate(ms[k][0]);uf.isolate(ms[k][1]);}}i = j;}List<Integer> res = new ArrayList<>();for (int i = 0; i < n; i++)if (uf.isConnected(i, 0))res.add(i);return res;}}