
最后一题明明挺简单的,脑子没转过来。。。
一个O(n^2)能过的题被我弄成了O(n^3)
5963. 反转两次的数字
显示英文描述
反转 一个整数意味着倒置它的所有位。
- 例如,反转 2021 得到 1202 。反转 12300 得到 321 ,不保留前导零 。
给你一个整数 num ,反转 num 得到 reversed1 ,接着反转 reversed1 得到 reversed2 。如果 reversed2 等于 num ,返回 true ;否则,返回 false 。
示例 1:
输入:num = 526 输出:true 解释:反转 num 得到 625 ,接着反转 625 得到 526 ,等于 num 。
示例 2:
输入:num = 1800 输出:false 解释:反转 num 得到 81 ,接着反转 81 得到 18 ,不等于 num 。
示例 3:
输入:num = 0 输出:true 解释:反转 num 得到 0 ,接着反转 0 得到 0 ,等于 num 。
提示:
- 0 <= num <= 106
思路:
反转再转回去,只需要看最后一位是不是0即可,0特判一下
class Solution {public boolean isSameAfterReversals(int num) {if (num % 10 == 0 && num != 0)return false;return true;}}
5964. 执行所有后缀指令
现有一个 n x n 大小的网格,左上角单元格坐标 (0, 0) ,右下角单元格坐标 (n - 1, n - 1) 。给你整数 n 和一个整数数组 startPos ,其中 startPos = [startrow, startcol] 表示机器人最开始在坐标为 (startrow, startcol) 的单元格上。
另给你一个长度为 m 、下标从 0 开始的字符串 s ,其中 s[i] 是对机器人的第 i 条指令:’L’(向左移动),’R’(向右移动),’U’(向上移动)和 ‘D’(向下移动)。
机器人可以从 s 中的任一第 i 条指令开始执行。它将会逐条执行指令直到 s 的末尾,但在满足下述条件之一时,机器人将会停止:
- 下一条指令将会导致机器人移动到网格外。
- 没有指令可以执行。
返回一个长度为 m 的数组 answer ,其中 answer[i] 是机器人从第 i 条指令 开始 ,可以执行的 指令数目 。
示例 1: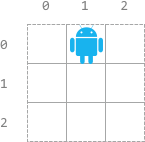
输入:n = 3, startPos = [0,1], s = “RRDDLU” 输出:[1,5,4,3,1,0] 解释:机器人从 startPos 出发,并从第 i 条指令开始执行: - 0: “R_RDDLU” 在移动到网格外之前,只能执行一条 “R” 指令。 - 1: “RDDLU“ 可以执行全部五条指令,机器人仍在网格内,最终到达 (0, 0) 。 - 2: “DDLU“ 可以执行全部四条指令,机器人仍在网格内,最终到达 (0, 0) 。 - 3: “DLU“ 可以执行全部三条指令,机器人仍在网格内,最终到达 (0, 0) 。 - 4: “LU” 在移动到网格外之前,只能执行一条 “L” 指令。 - 5: “U” 如果向上移动,将会移动到网格外。
示例 2: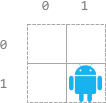
输入:n = 2, startPos = [1,1], s = “LURD” 输出:[4,1,0,0] 解释: - 0: “LURD“ - 1: “U_RD” - 2: “RD” - 3: “D”
示例 3:
输入:n = 1, startPos = [0,0], s = “LRUD” 输出:[0,0,0,0] 解释:无论机器人从哪条指令开始执行,都会移动到网格外。
提示:
- m == s.length
- 1 <= n, m <= 500
- startPos.length == 2
- 0 <= startrow, startcol < n
- s 由 ‘L’、’R’、’U’ 和 ‘D’ 组成
思路:
暴力计算即可
class Solution {Map<Character, Integer> map = new HashMap<>();public int[] executeInstructions(int n, int[] startPos, String s) {map.put('U', 0);map.put('R', 1);map.put('D', 2);map.put('L', 3);int m = s.length();int[] res = new int[m];char[] ch = s.toCharArray();for (int i = 0; i < m; i++) {res[i] = check(n, startPos, ch, i);}return res;}int[] dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};int check(int n, int[] s, char[] ch, int S) {int cnt = 0;int x = s[0], y = s[1];for (int i = S; i < ch.length; i++) {char c = ch[i];int idx = map.get(c);int a = x + dx[idx], b = y + dy[idx];if (a < 0 || a >= n || b < 0 || b >= n)break;cnt++;x = a;y = b;}return cnt;}}
5965. 相同元素的间隔之和
给你一个下标从 0 开始、由 n 个整数组成的数组 arr 。
arr 中两个元素的 间隔 定义为它们下标之间的 绝对差 。更正式地,arr[i] 和 arr[j] 之间的间隔是 |i - j| 。
返回一个长度为 n 的数组 intervals ,其中 intervals[i] 是 _arr[i] 和 arr 中每个相同元素(与 arr[i] 的值相同)的 间隔之和 。_
注意:|x| 是 x 的绝对值。
示例 1:
输入:arr = [2,1,3,1,2,3,3] 输出:[4,2,7,2,4,4,5] 解释: - 下标 0 :另一个 2 在下标 4 ,|0 - 4| = 4 - 下标 1 :另一个 1 在下标 3 ,|1 - 3| = 2 - 下标 2 :另两个 3 在下标 5 和 6 ,|2 - 5| + |2 - 6| = 7 - 下标 3 :另一个 1 在下标 1 ,|3 - 1| = 2 - 下标 4 :另一个 2 在下标 0 ,|4 - 0| = 4 - 下标 5 :另两个 3 在下标 2 和 6 ,|5 - 2| + |5 - 6| = 4 - 下标 6 :另两个 3 在下标 2 和 5 ,|6 - 2| + |6 - 5| = 5
示例 2:
输入:arr = [10,5,10,10] 输出:[5,0,3,4] 解释: - 下标 0 :另两个 10 在下标 2 和 3 ,|0 - 2| + |0 - 3| = 5 - 下标 1 :只有这一个 5 在数组中,所以到相同元素的间隔之和是 0 - 下标 2 :另两个 10 在下标 0 和 3 ,|2 - 0| + |2 - 3| = 3 - 下标 3 :另两个 10 在下标 0 和 2 ,|3 - 0| + |3 - 2| = 4
提示:
- n == arr.length
- 1 <= n <= 105
- 1 <= arr[i] <= 105
思路:
一个数学题
class Solution {public long[] getDistances(int[] arr) {int n = arr.length;int[] cl = new int[n];long[] left = new long[n];Map<Integer, Long> map = new HashMap<>();int[] cnt = new int[100010];for (int i = 0; i < n; i++) {cl[i] = cnt[arr[i]];cnt[arr[i]]++;left[i] = map.getOrDefault(arr[i], 0L);map.merge(arr[i], 1L * i, Long::sum);}long[] res = new long[n];for (int i = 0; i < n; i++) {long x = 1L * cl[i] * i - left[i];long sum = map.get(arr[i]);x += sum - left[i] - i - 1L * (cnt[arr[i]] - cl[i] - 1) * i * 1L;res[i] = x;}return res;}}
5966. 还原原数组
Alice 有一个下标从 0 开始的数组 arr ,由 n 个正整数组成。她会选择一个任意的 正整数 k 并按下述方式创建两个下标从 0 开始的新整数数组 lower 和 higher :
- 对每个满足 0 <= i < n 的下标 i ,lower[i] = arr[i] - k
- 对每个满足 0 <= i < n 的下标 i ,higher[i] = arr[i] + k
不幸地是,Alice 丢失了全部三个数组。但是,她记住了在数组 lower 和 higher 中出现的整数,但不知道每个整数属于哪个数组。请你帮助 Alice 还原原数组。
给你一个由 2n 个整数组成的整数数组 nums ,其中 恰好 n 个整数出现在 lower ,剩下的出现在 higher ,还原并返回 原数组 arr 。如果出现答案不唯一的情况,返回 任一 有效数组。
注意:生成的测试用例保证存在 至少一个 有效数组 arr 。
示例 1:
输入:nums = [2,10,6,4,8,12] 输出:[3,7,11] 解释: 如果 arr = [3,7,11] 且 k = 1 ,那么 lower = [2,6,10] 且 higher = [4,8,12] 。 组合 lower 和 higher 得到 [2,6,10,4,8,12] ,这是 nums 的一个排列。 另一个有效的数组是 arr = [5,7,9] 且 k = 3 。在这种情况下,lower = [2,4,6] 且 higher = [8,10,12] 。
示例 2:
输入:nums = [1,1,3,3] 输出:[2,2] 解释: 如果 arr = [2,2] 且 k = 1 ,那么 lower = [1,1] 且 higher = [3,3] 。 组合 lower 和 higher 得到 [1,1,3,3] ,这是 nums 的一个排列。 注意,数组不能是 [1,3] ,因为在这种情况下,获得 [1,1,3,3] 唯一可行的方案是 k = 0 。 这种方案是无效的,k 必须是一个正整数。
示例 3:
输入:nums = [5,435] 输出:[220] 解释: 唯一可行的组合是 arr = [220] 且 k = 215 。在这种情况下,lower = [5] 且 higher = [435] 。
提示:
- 2 * n == nums.length
- 1 <= n <= 1000
- 1 <= nums[i] <= 109
- 生成的测试用例保证存在 至少一个 有效数组 arr
思路:
排序,用每个数和最小的数作差就是所有可能的k的取值
比赛时我愣生生写了个双重循环去找,真是脑子秀逗了啊!虽然过了也是侥幸!
判断该k是否合法,若合法则输出最终结果。
时间复杂度:O(n2),空间复杂度:O(n)
class Solution {public int[] recoverArray(int[] nums) {Map<Integer, Integer> map = new HashMap<>();List<Integer> res = new ArrayList<>();int n = nums.length / 2;Arrays.sort(nums);for (int j = 1; j < 2 * n; j++) {int delta = nums[j] - nums[0];if (delta == 0 || delta % 2 != 0)continue;boolean flag = true;map.clear();for (int x : nums) {map.merge(x, 1, Integer::sum);}delta /= 2;res.clear();for (int i = 0; i < 2 * n && flag; i++) {if (map.get(nums[i]) > 0) {if (map.getOrDefault(nums[i] + 2 * delta, 0) == 0) {flag = false;break;} else {map.merge(nums[i], -1, Integer::sum);map.merge(nums[i] + 2 * delta, -1, Integer::sum);res.add(nums[i] + delta);}}}if (flag) {int[] ans = new int[n];for (int i = 0; i < n; i++)ans[i] = res.get(i);return ans;}}return null;}}

