🏆 第 290 场力扣周赛

我愿称之为离散化场！3和4都是差分 + 离散化，只不过一个1维，一个2维罢了，T4还比T3简单。。。

6041. 多个数组求交集

给你一个二维整数数组 nums ，其中 nums[i] 是由 不同 正整数组成的一个非空数组，按 升序排列 返回一个数组，数组中的每个元素在 nums 所有数组 中都出现过。

示例 1：
输入：nums = [[3,1,2,4,5],[1,2,3,4],[3,4,5,6]] 输出：[3,4] 解释： nums[0] = [3,1,2,4,5]，nums[1] = [1,2,3,4]，nums[2] = [3,4,5,6]，在 nums 中每个数组中都出现的数字是 3 和 4 ，所以返回 [3,4] 。
示例 2：
输入：nums = [[1,2,3],[4,5,6]] 输出：[] 解释： 不存在同时出现在 nums[0] 和 nums[1] 的整数，所以返回一个空列表 [] 。

提示：

• 1 <= nums.length <= 1000
• 1 <= sum(nums[i].length) <= 1000
• 1 <= nums[i][j] <= 1000
• nums[i] 中的所有值 互不相同

思路：
暴力模拟即可
时间复杂度：O(n2)

class Solution {
    public List<Integer> intersection(int[][] nums) {
        int n = nums.length, m = nums[0].length;
        List<Integer> res = new ArrayList<>();
        for (int x : nums[0]) {
            int cnt = 1;
            for (int i = 1; i < n; i++)
                for (int v : nums[i]) {
                    if (v == x) {
                        cnt++;
                        break;
                    }
                }
            if (cnt == n)
                res.add(x);
        }
        Collections.sort(res);
        return res;
    }
}
// 灵活调用API
//boolean retainAll(Collection<?> c)
class Solution {
    public List<Integer> intersection(int[][] nums) {
        Set<Integer> set = new HashSet<>();
        List<Integer> res = new ArrayList<>();
        for (int x : nums[0])
            set.add(x);
        for (int[] p : nums) {
            Set<Integer> t = new HashSet<>();
            for (int x : p) {
                t.add(x);
            }
            set.retainAll(t);
        }
        res.addAll(set);
        Collections.sort(res);
        return res;
    }
}

6042. 统计圆内格点数目

给你一个二维整数数组 circles ，其中 circles[i] = [xi, yi, ri] 表示网格上圆心为 (xi, yi) 且半径为 ri 的第 i 个圆，返回出现在 至少一个 圆内的 格点数目 。
注意：

• 格点 是指整数坐标对应的点。
• 圆周上的点 也被视为出现在圆内的点。

示例 1：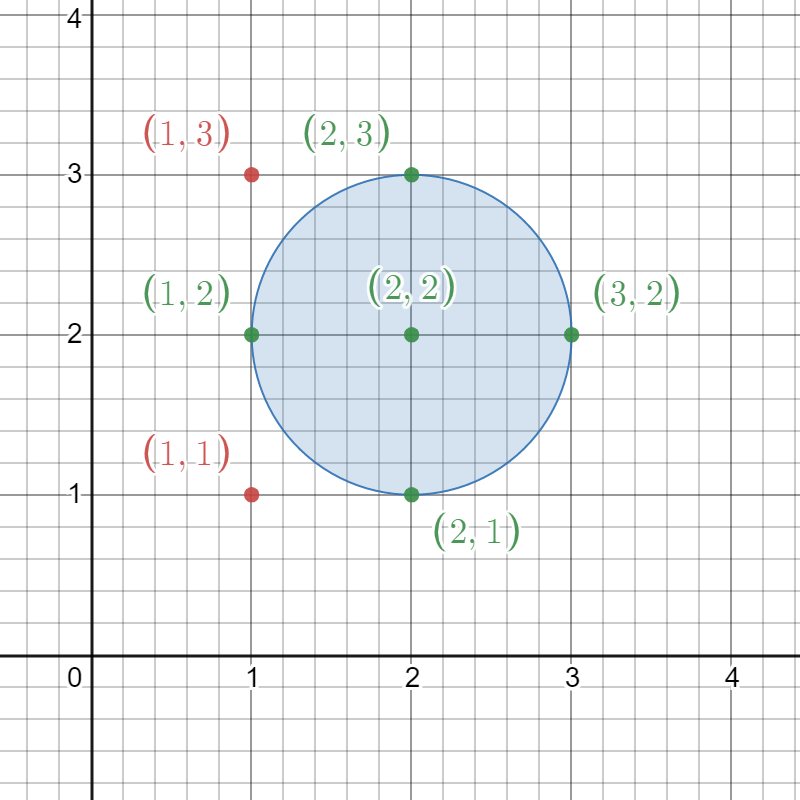

输入：circles = [[2,2,1]] 输出：5 解释： 给定的圆如上图所示。 出现在圆内的格点为 (1, 2)、(2, 1)、(2, 2)、(2, 3) 和 (3, 2)，在图中用绿色标识。 像 (1, 1) 和 (1, 3) 这样用红色标识的点，并未出现在圆内。 因此，出现在至少一个圆内的格点数目是 5 。
示例 2：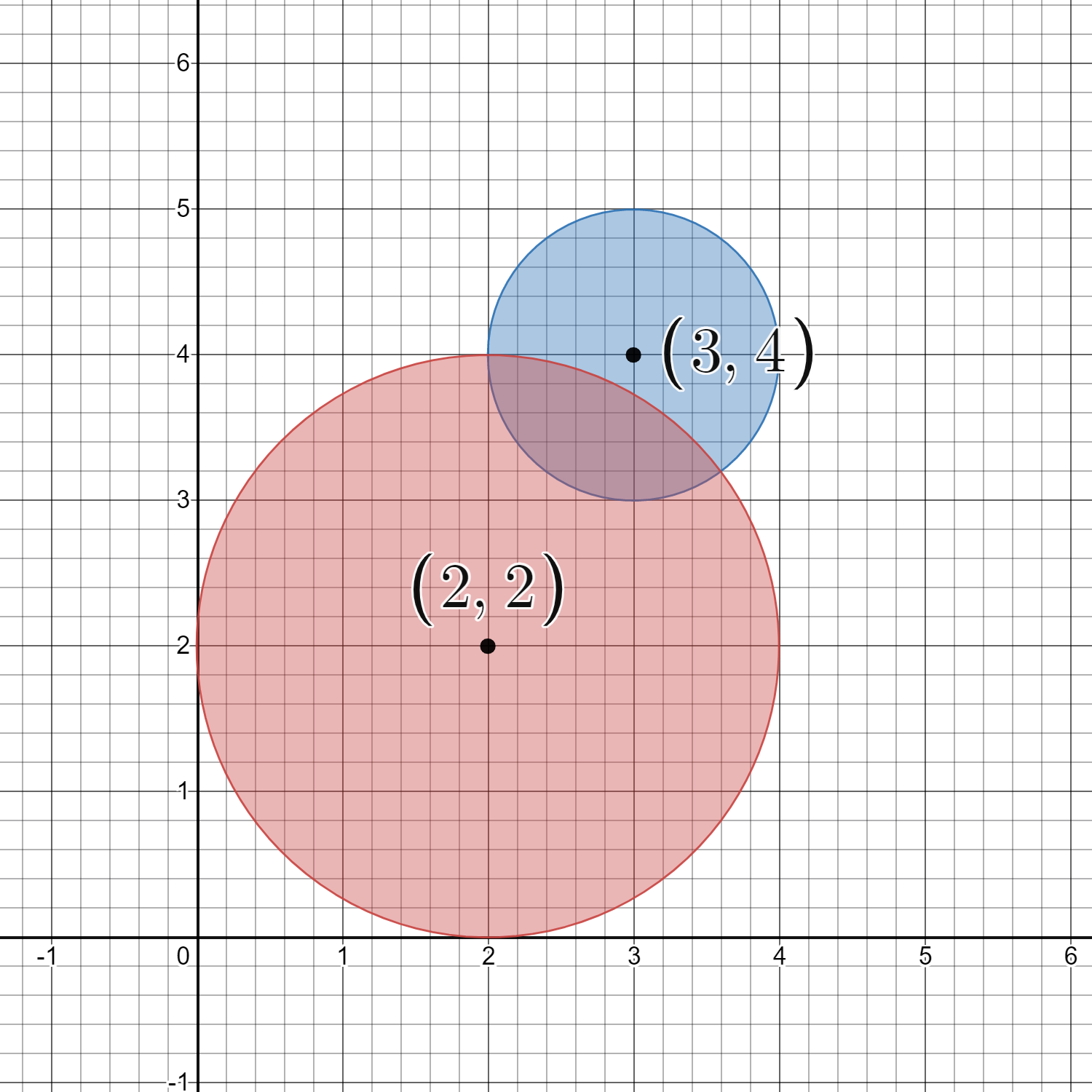

输入：circles = [[2,2,2],[3,4,1]] 输出：16 解释： 给定的圆如上图所示。 共有 16 个格点出现在至少一个圆内。 其中部分点的坐标是 (0, 2)、(2, 0)、(2, 4)、(3, 2) 和 (4, 4) 。

提示：

• 1 <= circles.length <= 200
• circles[i].length == 3
• 1 <= xi, yi <= 100
• 1 <= ri <= min(xi, yi)

思路：
范围不大，暴力找点即可
时间复杂度：O(n3), n <= 200

class Solution {
    public int countLatticePoints(int[][] circles) {
        boolean[][] st = new boolean[300][300];
        for (int[] c : circles) {
            int x = c[0], y = c[1], r = c[2];
            for (int i = x - r; i <= x + r; i++) {
                for (int j = y - r; j <= y + r; j++) {
                    if (check(i, j, x, y, r))
                        st[i][j] = true;
                }
            }
        }
        int cnt = 0;
        for (int i = 0; i < 300; i++) {
            for (int j = 0; j < 300; j++) {
                if (st[i][j])
                    cnt++;
            }
        }
        return cnt;
    }
    boolean check(int x1, int y1, int x2, int y2, int r) {
        int x = (x1 - x2), y = (y1 - y2);
        if (x * x + y * y <= r * r)
            return true;
        else
            return false;
    }
}
// 更简单的写法
class Solution {
    public int countLatticePoints(int[][] circles) {
        int ret = 0;
        for(int x = 0;x <= 200;x++){
            for(int y = 0;y <= 200;y++){                
                for(int[] c : circles){
                    if((c[0] - x) * (c[0] - x) + (c[1] - y) * (c[1] - y) <= c[2]*c[2]){
                        ret++;
                        break;
                    }
                }
            }
        }
        return ret;
    }
}

6043. 统计包含每个点的矩形数目

给你一个二维整数数组 rectangles ，其中 rectangles[i] = [li, hi] 表示第 i 个矩形长为 li 高为 hi 。给你一个二维整数数组 points ，其中 points[j] = [xj, yj] 是坐标为 (xj, yj) 的一个点。
第 i 个矩形的 左下角 在 (0, 0) 处，右上角 在 (li, hi) 。
请你返回一个整数数组 _count ，长度为 points.length，其中 count[j]是 包含 第 _j 个点的矩形数目。
如果 0 <= xj <= li 且 0 <= yj <= hi ，那么我们说第 i 个矩形包含第 j 个点。如果一个点刚好在矩形的 边上 ，这个点也被视为被矩形包含。

示例 1：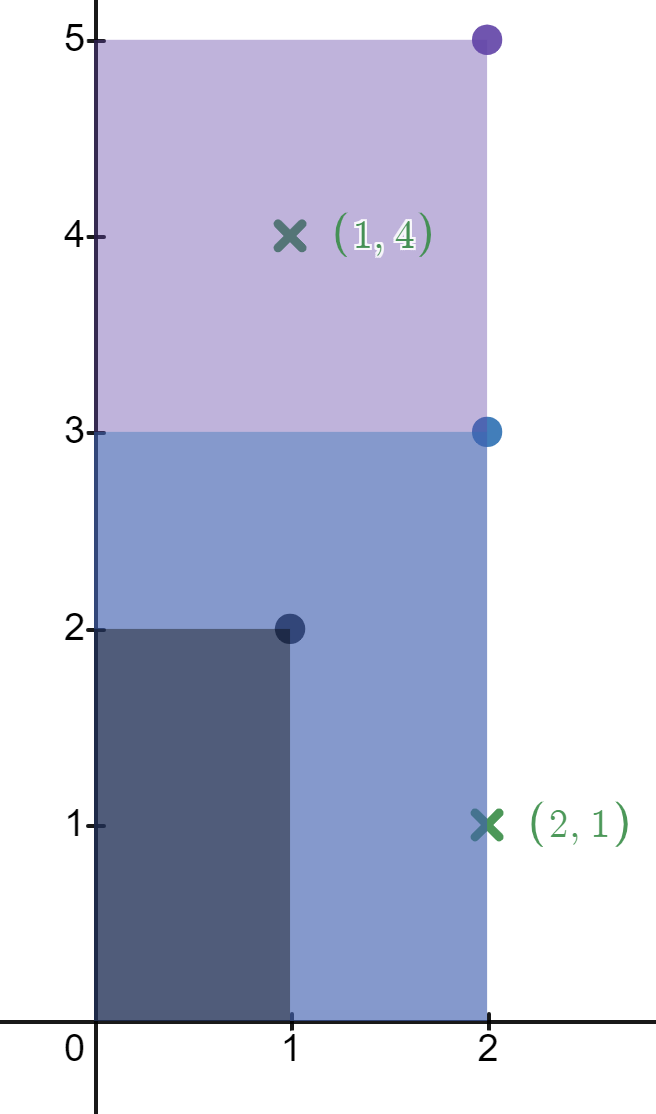

输入：rectangles = [[1,2],[2,3],[2,5]], points = [[2,1],[1,4]] 输出：[2,1] 解释： 第一个矩形不包含任何点。 第二个矩形只包含一个点 (2, 1) 。 第三个矩形包含点 (2, 1) 和 (1, 4) 。 包含点 (2, 1) 的矩形数目为 2 。 包含点 (1, 4) 的矩形数目为 1 。 所以，我们返回 [2, 1] 。
示例 2：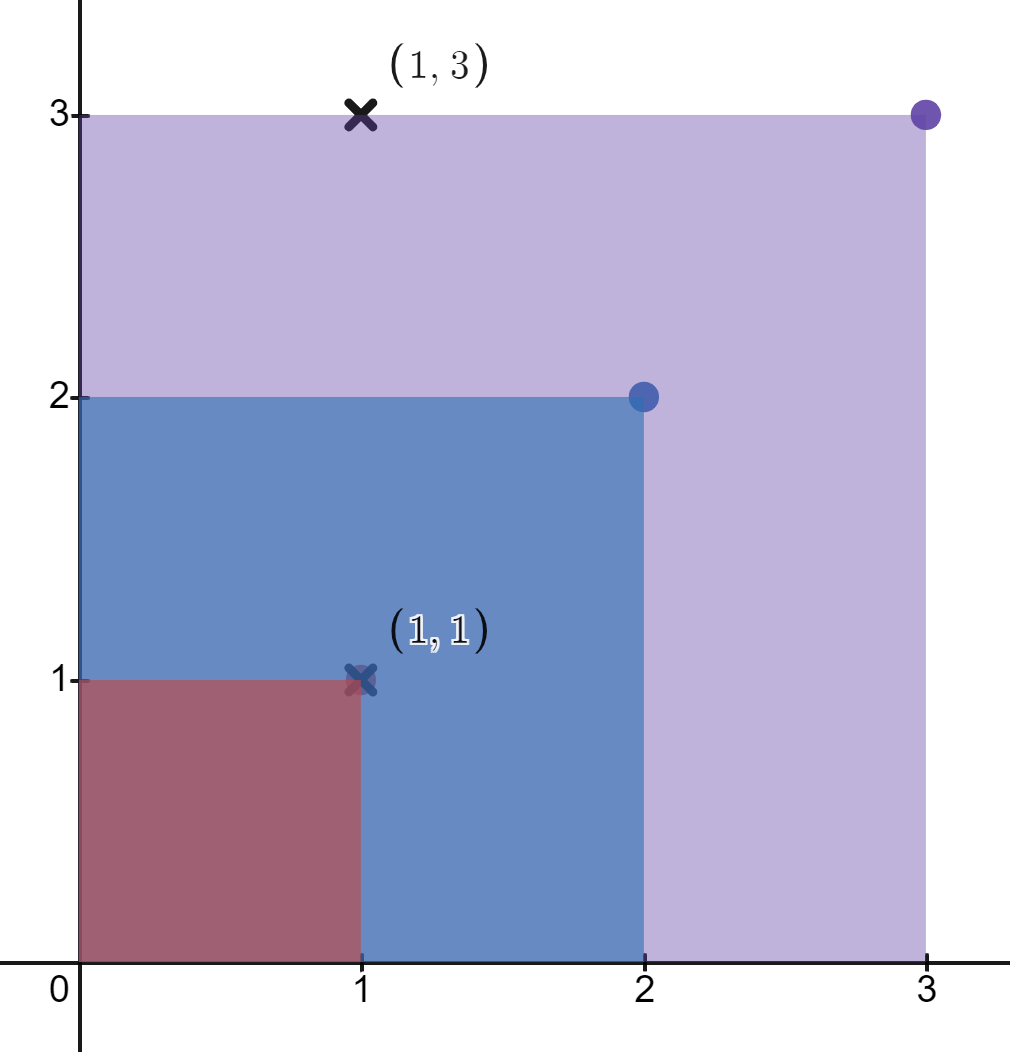

输入：rectangles = [[1,1],[2,2],[3,3]], points = [[1,3],[1,1]] 输出：[1,3] 解释： 第一个矩形只包含点 (1, 1) 。 第二个矩形只包含点 (1, 1) 。 第三个矩形包含点 (1, 3) 和 (1, 1) 。 包含点 (1, 3) 的矩形数目为 1 。 包含点 (1, 1) 的矩形数目为 3 。 所以，我们返回 [1, 3] 。

提示：

• 1 <= rectangles.length, points.length <= 5 * 104
• rectangles[i].length == points[j].length == 2
• 1 <= li, xj <= 109
• 1 <= hi, yj <= 100
• 所有 rectangles 互不相同 。
• 所有 points 互不相同 。

思路：
h和y的范围都很小，而l和x的范围很大，需要离散化
然后用二维差分即可
时间复杂度：O(nlogn)
空间复杂度：O(n)

class Solution {
    TreeSet<Integer> set = new TreeSet<>();
    Map<Integer, Integer> map = new HashMap<>();
    public int[] countRectangles(int[][] r, int[][] points) {
        int n = points.length;
        int[] res = new int[n];
        for (int[] x : r) {
            set.add(x[0]);
            set.add(x[0] + 1);
        }
        for (int[] p : points) {
            int x = p[0], y = p[1];
            set.add(x);
        }
        map.put(0, 0);
        int idx = 1;
        for (int x : set)
            if (x != 0)
                map.put(x, idx++);
        int row = map.size();
        int[][] a = new int[row + 1][110];
        for (int[] p : r) {
            int x = map.get(p[0]), y = p[1];
            a[0][0]++;
            a[0][y + 1]--;
            a[x + 1][0]--;
            a[x + 1][y + 1]++;
        }
        for (int i = 0; i <= row; i++) {
            for (int j = 0; j < 110; j++) {
                if (i > 0)
                    a[i][j] += a[i - 1][j];
                if (j > 0)
                    a[i][j] += a[i][j - 1];
                if (i > 0 && j > 0)
                    a[i][j] -= a[i - 1][j - 1];
            }
        }
        for (int i = 0; i < n; i++) {
            int x = map.get(points[i][0]), y = points[i][1];
            res[i] = a[x][y];
        }
        return res;
    }
}
// 更简单的写法
class Solution {
    public int[] countRectangles(int[][] rectangles, int[][] points) {
        int n = rectangles.length, Q = points.length;
        int[][] a = new int[n + Q][];
        for (int i = 0; i < n; i++) {
            a[i] = new int[]{rectangles[i][0], rectangles[i][1]};
        }
        for (int i = 0; i < Q; i++) {
            a[i + n] = new int[]{points[i][0], points[i][1], i};
        }
        Arrays.sort(a, (o1, o2) -> {
            if (o1[0] != o2[0])
                return o2[0] - o1[0];
            else
                return o1.length - o2.length;
        });
        int[] res = new int[Q];
        int[] cnt = new int[110];
        for (int[] p : a) {
            if (p.length == 3)
                res[p[2]] = cnt[p[1]];
            else {
                for (int i = 0; i <= p[1]; i++)
                    cnt[i]++;
            }
        }
        return res;
    }
}

6044. 花期内花的数目

给你一个下标从 0 开始的二维整数数组 flowers ，其中 flowers[i] = [starti, endi] 表示第 i 朵花的 花期 从 starti 到 endi （都 包含）。同时给你一个下标从 0 开始大小为 n 的整数数组 persons ，persons[i] 是第 i 个人来看花的时间。
请你返回一个大小为 n 的整数数组_ _answer ，其中 answer[i]是第 i 个人到达时在花期内花的 数目 。

示例 1：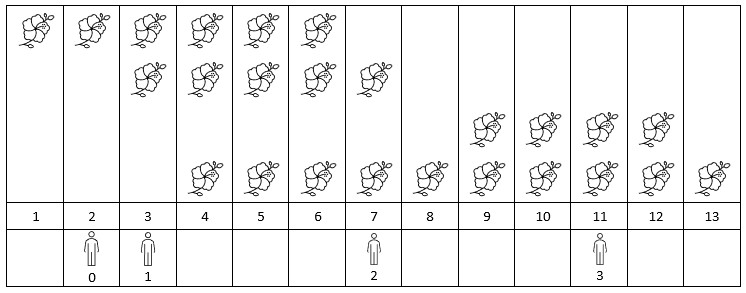

输入：flowers = [[1,6],[3,7],[9,12],[4,13]], persons = [2,3,7,11] 输出：[1,2,2,2] 解释：上图展示了每朵花的花期时间，和每个人的到达时间。 对每个人，我们返回他们到达时在花期内花的数目。
示例 2：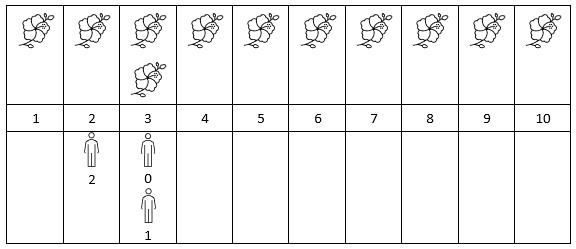

输入：flowers = [[1,10],[3,3]], persons = [3,3,2] 输出：[2,2,1] 解释：上图展示了每朵花的花期时间，和每个人的到达时间。 对每个人，我们返回他们到达时在花期内花的数目。

提示：

• 1 <= flowers.length <= 5 * 104
• flowers[i].length == 2
• 1 <= starti <= endi <= 109
• 1 <= persons.length <= 5 * 104
• 1 <= persons[i] <= 109

思路：
离散化 + 差分
时间复杂度：O(nlogn)
空间复杂度：O(n)

class Solution {
    TreeSet<Integer> set = new TreeSet<>();
    Map<Integer, Integer> map = new HashMap<>();
    public int[] fullBloomFlowers(int[][] f, int[] p) {
        for (int[] x : f) {
            set.add(x[0]);
            set.add(x[1] + 1);
        }
        for (int x : p) {
            set.add(x);
        }
        int idx = 0;
        for (int x : set)
            map.put(x, idx++);
        int[] a = new int[idx];
        for (int[] x : f) {
            a[map.get(x[0])]++;
            a[map.get(x[1] + 1)]--;
        }
        for (int i = 1; i < idx; i++)
            a[i] += a[i - 1];
        int[] res = new int[p.length];
        for (int i = 0; i < p.length; i++) {
            res[i] = a[map.get(p[i])];
        }
        return res;
    }
}

// 更简单的写法
class Solution {
    TreeMap<Integer, Integer> map = new TreeMap<>();
    public int[] fullBloomFlowers(int[][] f, int[] p) {
        for (int[] x : f) {
            map.merge(x[0], 1, Integer::sum);
            map.merge(x[1] + 1, -1, Integer::sum);
        }
        for (int x : p)
            map.merge(x, 0, Integer::sum);
        int pre = 0;
        for (int x : map.keySet()) {
            pre += map.get(x);
            map.put(x, pre);
        }
        int[] res = new int[p.length];
        for (int i = 0; i < p.length; i++) {
            res[i] = map.get(p[i]);
        }
        return res;
    }
}

// 扫描线
class Solution {
    public int[] fullBloomFlowers(int[][] flowers, int[] persons) {
        int n = flowers.length,  m = persons.length;
        int[][] a = new int[2 * n + m][];
        for (int i = 0; i < n; i++) {
            int l = flowers[i][0], r = flowers[i][1];
            a[i] = new int[]{l, 1};
            a[i + n] = new int[]{r + 1, -1};
        }
        for (int i = 0, j = 2 * n; i < m; i++, j++)
            a[j] = new int[]{persons[i], 0, i};
        Arrays.sort(a, (o1, o2) -> {
            if (o1[0] != o2[0])
                return o1[0] - o2[0];
            else
                return o1.length - o2.length;
        });
        int[] res = new int[m];
        int pre = 0;
        for (int i = 0; i < 2 * n + m; i++) {
            pre += a[i][1];
            if (a[i].length == 3)
                res[a[i][2]] = pre;
        }
        return res;
    }
}