DP - 图上DP - 《学习笔记》

787. K 站中转内最便宜的航班

有 n 个城市通过一些航班连接。给你一个数组 flights ，其中 flights[i] = [fromi, toi, pricei] ，表示该航班都从城市 fromi 开始，以价格 pricei 抵达 toi。
现在给定所有的城市和航班，以及出发城市 src 和目的地 dst，你的任务是找到出一条最多经过 k 站中转的路线，使得从 src 到 dst 的 价格最便宜 ，并返回该价格。如果不存在这样的路线，则输出 -1。

示例 1：
输入: n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]] src = 0, dst = 2, k = 1 输出: 200 解释: 城市航班图如下从城市 0 到城市 2 在 1 站中转以内的最便宜价格是 200，如图中红色所示。
示例 2：
输入: n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]] src = 0, dst = 2, k = 0 输出: 500 解释: 城市航班图如下从城市 0 到城市 2 在 0 站中转以内的最便宜价格是 500，如图中蓝色所示。

提示：

1 <= n <= 100
0 <= flights.length <= (n * (n - 1) / 2)
flights[i].length == 3
0 <= fromi, toi < n
fromi != toi
1 <= pricei <= 104
航班没有重复，且不存在自环
0 <= src, dst, k < n
src != dst

思路：
方法1：DP
状态表示：f[i][j]表示经过i条边到达j的所有花费的集合。
属性：最小花费
状态转移：当最后处在j点时，考虑倒数第二点的位置k，是所有能一步到j点的所以点。
f[i][j] = Math.min(f[i - 1][k], f[i][j]) (k, j) ∈ flights
初始化：f[0][src] = 0
空间优化：考虑到f[i][j]只与f[i - 1][k]有关，故可用一维数组进行优化

class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        int[] dist = new int[n];
        Arrays.fill(dist, 0x3f3f3f3f);
        dist[src] = 0;
        int[] back = new int[n];
        for (int i = 0; i <= k; i++) {
            back = Arrays.copyOf(dist, n);
            for (int[] edges : flights) {
                int a = edges[0], b = edges[1], c = edges[2];
                dist[b] = Math.min(dist[b], back[a] + c);
            }
        }
        if (dist[dst] >= 0x3f3f3f3f) return -1;
        return dist[dst];   
    }
}

方法2：SPFA(不带优化)
不带st数组判重，本质还是Bellman-Ford

class Solution {
    int N = 10010;
    int[] h = new int[N], e = new int[N], w = new int[N], ne = new int[N];
    int n, idx;
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        Arrays.fill(h, -1);
        this.n = n;
        for (int[] p : flights) {
            int a = p[0], b = p[1], c = p[2];
            add(a, b, c);
        }
        int[] dist = new int[n];
        Arrays.fill(dist, 0x3f3f3f3f);
        dist[src] = 0;
        // pos cnt fee
        Queue<int[]> q = new LinkedList<>();
        q.offer(new int[]{src, 0, 0});
        boolean[] st = new boolean[n];
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int cur = p[0], cnt = p[1], fee = p[2];
            if (p[1] > k) break;
            for (int i = h[cur]; i != -1; i = ne[i]) {
                int j = e[i], cost = w[i];
                if (cost + fee < dist[j]) {
                    dist[j] = cost + fee;
                    q.offer(new int[]{j, cnt + 1, cost + fee});
                }
            }
        }
        return dist[dst] >= 0x3f3f3f3f ? -1 : dist[dst];
    }
    void add(int a, int b, int c) {
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}

方法3：堆优化版Dijkstra
最小堆按最小花费来排序。
可能存在这样一种情况，有边数限制的情况下能从起点到终点，但花费超过了不考虑边数的最小花费。
所以更新边的时候需要考虑，尽管到该点的花费变多，但如果边数更少的话，可能对最终结果是有利的。
还有就是最终结果可能是处于最短边和最小花费的中间情况，这也是为什么用小根堆的原因之一。能保证花费少的先出队，而不是边数少的先出队

class Solution {
    int N = 10010;
    int[] h = new int[N], e = new int[N], w = new int[N], ne = new int[N];
    int n, idx;
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        Arrays.fill(h, -1);
        this.n = n;
        for (int[] p : flights) {
            int a = p[0], b = p[1], c = p[2];
            add(a, b, c);
        }
        int[] dist = new int[n];
        Arrays.fill(dist, 0x3f3f3f3f);
        dist[src] = 0;
        // pos cnt fee
        PriorityQueue<int[]> q = new PriorityQueue<>((o1, o2) -> o1[2] - o2[2]);
        q.offer(new int[]{src, 0, 0});
        int[] count = new int[n];
        Arrays.fill(count, 0x3f3f3f3f);
        count[src] = 0;
        k++;
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int cur = p[0], cnt = p[1], fee = p[2];
            if (cnt + 1 > k) continue;
            for (int i = h[cur]; i != -1; i = ne[i]) {
                int j = e[i], cost = w[i];
                if (dist[j] > cost + fee) {
                    dist[j] = cost + fee;
                    count[j] = cnt + 1;
                    q.offer(new int[]{j, cnt + 1, fee + cost});
                } else if (cnt + 1 <= count[j]) {
                    count[j] = cnt + 1;
                    q.offer(new int[]{j, cnt + 1, fee + cost});
                }
            }
        }
        return dist[dst] >= 0x3f3f3f3f ? -1 : dist[dst];
    }
    void add(int a, int b, int c) {
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}

1928. 规定时间内到达终点的最小花费

一个国家有 n 个城市，城市编号为 0 到 n - 1 ，题目保证 所有城市 都由双向道路 连接在一起 。道路由二维整数数组 edges 表示，其中 edges[i] = [xi, yi, timei] 表示城市 xi 和 yi 之间有一条双向道路，耗费时间为 timei 分钟。两个城市之间可能会有多条耗费时间不同的道路，但是不会有道路两头连接着同一座城市。
每次经过一个城市时，你需要付通行费。通行费用一个长度为 n 且下标从 0 开始的整数数组 passingFees 表示，其中 passingFees[j] 是你经过城市 j 需要支付的费用。
一开始，你在城市 0 ，你想要在 maxTime 分钟以内 （包含 maxTime 分钟）到达城市 n - 1 。旅行的费用为你经过的所有城市 通行费之和 （包括起点和终点城市的通行费）。
给你 maxTime，edges 和 passingFees ，请你返回完成旅行的 最小费用 ，如果无法在 maxTime 分钟以内完成旅行，请你返回 -1 。

示例 1：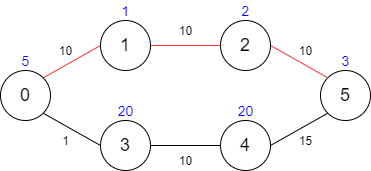

输入：maxTime = 30, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3] 输出：11 解释：最优路径为 0 -> 1 -> 2 -> 5 ，总共需要耗费 30 分钟，需要支付 11 的通行费。
示例 2：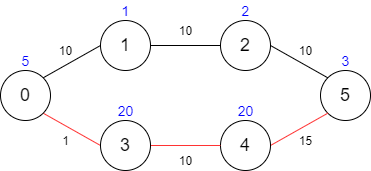

输入：maxTime = 29, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3] 输出：48 解释：最优路径为 0 -> 3 -> 4 -> 5 ，总共需要耗费 26 分钟，需要支付 48 的通行费。你不能选择路径 0 -> 1 -> 2 -> 5 ，因为这条路径耗费的时间太长。
示例 3：
输入：maxTime = 25, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3] 输出：-1 解释：无法在 25 分钟以内从城市 0 到达城市 5 。

提示：

1 <= maxTime <= 1000
n == passingFees.length
2 <= n <= 1000
n - 1 <= edges.length <= 1000
0 <= xi, yi <= n - 1
1 <= timei <= 1000
1 <= passingFees[j] <= 1000
图中两个节点之间可能有多条路径。
图中不含有自环。

思路：
带限制的最短路问题。从起点到终点所有总时间不超过maxTime的路径中选择一条花费最少的路径。
方法1：DP
状态表示： f[t][i]表示使用恰好 t 分钟到达城市 i 需要的最少通行费总和。
状态转移：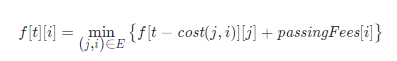

class Solution {
    public int minCost(int maxTime, int[][] edges, int[] passingFees) {
        int n = passingFees.length;
        int[][] f = new int[maxTime + 1][n]; // f[i][j]表示费时为i到达j的最小开销
        for (int i = 0; i <= maxTime; i++)
            Arrays.fill(f[i], 0x3f3f3f3f); 
        for (int i = 0; i <= maxTime; i++)
            f[i][0] = passingFees[0];       //f[i][0]表示费时i一直在起点状态的最小开销为passingfees[0]
        for (int i = 1; i <= maxTime; i++) {
            for (int[] edge : edges) {
                int a = edge[0], b = edge[1], w = edge[2];
                if (i >= w) {
                    f[i][b] = Math.min(f[i][b], f[i - w][a] + passingFees[b]);
                    f[i][a] = Math.min(f[i][a], f[i - w][b] + passingFees[a]);
                }
            }
        }
        int res = 0x3f3f3f3f;
        for (int i = 0; i <= maxTime; i++)
            res = Math.min(res, f[i][n - 1]);
        if (res == 0x3f3f3f3f) return -1;
        return res;
    }
}

方法2：dijkstra<br />类似于787的dijkstra<br />从起点到终点所有总时间不超过maxTime的路径中选择一条花费最少的路径。<br />将花费作为优先队列的排序依据。<br />有可能出现这样一种情况：在maxTime的时间要求下能到目的地，但花费超过不考虑到达时间的最小花费。

class Solution {
    int N = 2010;
    int[] h = new int[N], e = new int[N], ne = new int[N], w = new int[N];
    int n, idx;
    public int minCost(int maxTime, int[][] edges, int[] passingFees) {
        n = passingFees.length;
        Arrays.fill(h, -1);
        for (int[] edge : edges) {
            int a= edge[0], b = edge[1], c = edge[2];
            add(a, b, c);
            add(b, a, c);
        }
        int[] time = new int[n];
        Arrays.fill(time, 0x3f3f3f3f);
        time[0] = 0;
        int[] dist = new int[n];
        Arrays.fill(dist, 0x3f3f3f3f);
        dist[0] = passingFees[0];
        // pos, time, fee
        PriorityQueue<int[]> q = new PriorityQueue<>((o1, o2) -> o1[2] - o2[2]);
        q.offer(new int[]{0, 0, passingFees[0]});
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int cur = p[0], t = p[1], fee = p[2];
            for (int i = h[cur]; i != -1; i = ne[i]) {
                int j = e[i], cost = passingFees[j], c = w[i];
                if (c + t > maxTime) continue;
                if (dist[j] > cost + fee) {
                    dist[j] = cost + fee;
                    time[j] = c + t;
                    q.offer(new int[]{j, c + t, cost + fee});
                } else if (c + t < time[j]) {
                    time[j] = c + t;
                    q.offer(new int[]{j, c + t, cost + fee});
                }
            }
        }
        return dist[n - 1] >= 0x3f3f3f3f ? -1 : dist[n - 1];
    }
    void add(int a, int b, int c) {
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}

方法3：做完LCP 35后类似的拆点法
只是时间复杂度太高了，空间复杂度也很高，不如方法2

class Solution {
    int N = 2010;
    int[] h = new int[N], e = new int[N], ne = new int[N], w = new int[N];
    int n, idx;
    public int minCost(int maxTime, int[][] edges, int[] passingFees) {
        n = passingFees.length;
        Arrays.fill(h, -1);
        for (int[] edge : edges) {
            int a= edge[0], b = edge[1], c = edge[2];
            add(a, b, c);
            add(b, a, c);
        }
        int[][] dist = new int[n][maxTime + 1];
        for (int i = 1; i < n; i++)
            Arrays.fill(dist[i], 0x3f3f3f3f);
        Arrays.fill(dist[0], passingFees[0]);
        boolean[][] st = new boolean[n][maxTime + 1];
        // pos, time, fee
        PriorityQueue<int[]> q = new PriorityQueue<>((o1, o2) -> o1[2] - o2[2]);
        q.offer(new int[]{0, 0, passingFees[0]});
        int ans = -1;
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int cur = p[0], time = p[1], fee = p[2];
            if (st[cur][time]) continue;
            st[cur][time] = true;
            if (cur == n - 1) {
                ans = fee;
                break;
            }
            for (int i = h[cur]; i != -1; i = ne[i]) {
                int j = e[i], path = w[i];
                int t = time + path, cost = fee + passingFees[j];
                if (t <= maxTime && dist[j][t] > cost) {
                    dist[j][t] = cost;
                    q.offer(new int[]{j, t, cost});
                }
            }
        }
        return ans;
    }
    void add(int a, int b, int c) {
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}

LCP 35. 电动车游城市

小明的电动车电量充满时可行驶距离为 cnt，每行驶 1 单位距离消耗 1 单位电量，且花费 1 单位时间。小明想选择电动车作为代步工具。地图上共有 N 个景点，景点编号为 0 ~ N-1。他将地图信息以 [城市 A 编号,城市 B 编号,两城市间距离] 格式整理在在二维数组 paths，表示城市 A、B 间存在双向通路。初始状态，电动车电量为 0。每个城市都设有充电桩，charge[i] 表示第 i 个城市每充 1 单位电量需要花费的单位时间。请返回小明最少需要花费多少单位时间从起点城市 start 抵达终点城市 end。
示例 1：
输入：paths = [[1,3,3],[3,2,1],[2,1,3],[0,1,4],[3,0,5]], cnt = 6, start = 1, end = 0, charge = [2,10,4,1]
输出：43
解释：最佳路线为：1->3->0。
在城市 1 仅充 3 单位电至城市 3，然后在城市 3 充 5 单位电，行驶至城市 5。
充电用时共 310 + 51= 35
行驶用时 3 + 5 = 8，此时总用时最短 43。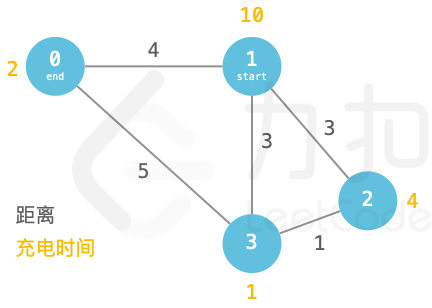

示例 2：
输入：paths = [[0,4,2],[4,3,5],[3,0,5],[0,1,5],[3,2,4],[1,2,8]], cnt = 8, start = 0, end = 2, charge = [4,1,1,3,2]
输出：38
解释：最佳路线为：0->4->3->2。
城市 0 充电 2 单位，行驶至城市 4 充电 8 单位，行驶至城市 3 充电 1 单位，最终行驶至城市 2。
充电用时 42+28+31 = 27
行驶用时 2+5+4 = 11，总用时最短 38。
*提示：

1 <= paths.length <= 200
paths[i].length == 3
2 <= charge.length == n <= 100
0 <= path[i][0],path[i][1],start,end < n
1 <= cnt <= 100
1 <= path[i][2] <= cnt
1 <= charge[i] <= 100
题目保证所有城市相互可以到达

思路：拆点 + dijkstra
本题需要考虑的问题是在当前点充不充电，如果充电，充多少电？
我们将(pos, power)二元组视为节点，然后建图，以(start,0)为起点跑一遍Dijkstra即可得到结果。
新图的节点数为图上DP - 图5 ，边数为图上DP - 图6 。C为最大电量，M为原来的边数。

class Solution {
    int N = 410;
    int[] h = new int[N], e = new int[N], ne = new int[N], w = new int[N];
    int n, idx;
    public int electricCarPlan(int[][] paths, int cnt, int start, int end, int[] charge) {
        n = charge.length;
        Arrays.fill(h, -1);
        for (int[] p : paths) {
            int a = p[0], b = p[1], c = p[2];
            add(a, b, c);
            add(b, a, c);
        }
        int[][] dist = new int[n][cnt + 1];
        for (int i = 0; i < n; i++)
            Arrays.fill(dist[i], 0x3f3f3f3f);
        dist[start][0] = 0;
        boolean[][] st = new boolean[n][cnt + 1];
        // pos, power, time
        PriorityQueue<int[]> q = new PriorityQueue<>((o1, o2) -> (o1[2] - o2[2]));
        q.offer(new int[]{start, 0, 0});
        int ans = 0;
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int cur = p[0], power = p[1], time = p[2];
            if (st[cur][power]) continue;
            st[cur][power] = true;
            if (cur == end) {
                ans = time;
                break;
            }
            // 充一次电
            if (power < cnt && time + charge[cur] < dist[cur][power + 1]) {
                dist[cur][power + 1] = time + charge[cur];
                q.offer(new int[]{cur, power + 1, time + charge[cur]});
            }
            //去其它点
            for (int i = h[cur]; i != -1; i = ne[i]) {
                int j = e[i], path = w[i];
                if (power >= path && dist[j][power - path] > time + path) {
                    dist[j][power - path] = time + path;
                    q.offer(new int[]{j, power - path, time + path});
                }
            }
        }
        return ans;
    }
    void add(int a, int b, int c) {
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}

小美的区域会议

小美是美团总部的高管，她想要召集一些美团的区域负责人来开会，已知美团的业务区域划分可以用一棵树来表示，树上有 n 个节点，每个节点分别代表美团的一个业务区域，每一个区域有一个负责人，这个负责人的级别为 A[i]
已知小美召集人员开会必须满足以下几个条件：
1.小美召集的负责人所在的区域必须构成一个非空的连通的图，即选取树上的一个连通子图。
2.这些负责人中，级别最高的和级别最低的相差不超过 k 。
请问小美有多少种召集负责人的方式，当且仅当选取的集合不同时我们就认为两种方式不同。由于方案数可能非常大，所以请对 10^9+7 取模。

输入：
- 输入第一行包含两个整数 n 和 k ，表示区域的数量，和不能超过的级别。
- 接下来有 n-1 行，每行有两个正整数 a 和 b ，表示 a 号区域和 b 号区域有一条边。
- 最后一行有 n 个整数，第 i 个整数表示 i 号区域负责人的级别。
输出：
- 输出仅包含一个整数，表示可以选择的方案数对 10^9+7 取模之后的结果。
示例：

输入：
5 1
1 2
2 3
3 4
4 5
2 2 2 2 2
输出：15
解释：显然一个区域的方案有 {1}，{2}，{3}，{4}，{5}，两个区域的方案有 4 个，三个区域的方案有 3 个，四个区域的方案有 2 个，五个区域的方案有 1 个，共 15 个。
提示：
1 <= n, k <= 2000
1 <= a, b <= n

思路：
一个树上DP问题，当然不能直接深度优先一次解决，因为与等级k有关，无法利用等级最大值和最小值进行状态转移
需要暴力DP，考虑每一个节点作为组中等级最小的成员，然后进行树形DP，当有和他等级一致的节点时，只选比它下标大的，这样做防止重复

import java.util.*;
public class Main {
    static final int MOD = (int)(1e9 + 7);
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(), k = sc.nextInt();
        List<Integer>[] edges = new ArrayList[n];
        for (int i = 0; i < n; i++)
            edges[i] = new ArrayList<>();
        for (int i = 1; i < n; i++) {
            int a = sc.nextInt() - 1, b = sc.nextInt() - 1;
            edges[a].add(b);
            edges[b].add(a);
        }
        int[] a = new int[n];
        for (int i = 0; i < n; i++) {
            a[i] = sc.nextInt();
        }
        int res = 0;
        for (int i = 0; i < n; i++)
            //第一个i表示当前节点，第二个i表示本次深搜的依据节点，其他节点等级必须大于等于i的等级，如果等级一致则下标必须大于i，最后一个参数表示其从哪个节点转移过来的，防止自环
            res = (res + dfs(edges, i, i, a, k, -1)) % MOD;    
        System.out.println(res);
    }
    static int dfs(List<Integer>[] edges, int u, int o, int[] a, int k, int fa) {
        long cnt = 1;
        for (int ne : edges[u]) {
            if (fa == ne) continue;
            int x = a[ne] - a[o];
            if (x == 0 && ne > o || x > 0 && x <= k)
                cnt = (cnt * (dfs(edges, ne, o, a, k, u) + 1)) % MOD;
        }
        return (int)(cnt % MOD);
    }
}