归并排序

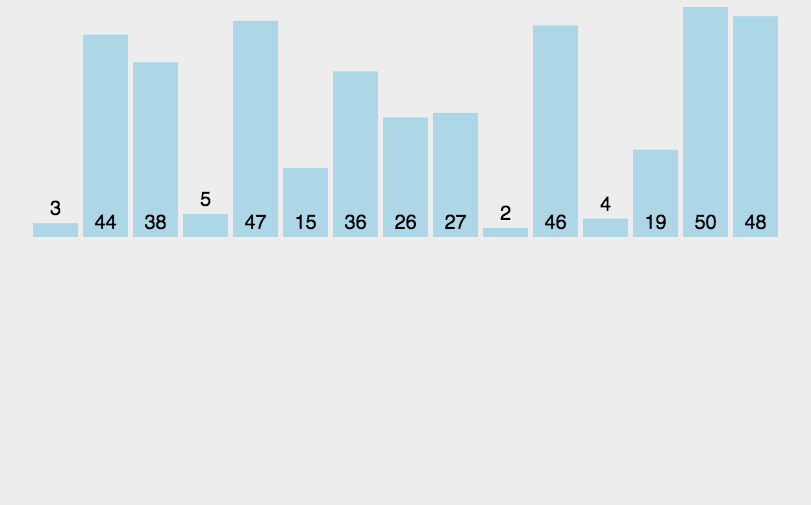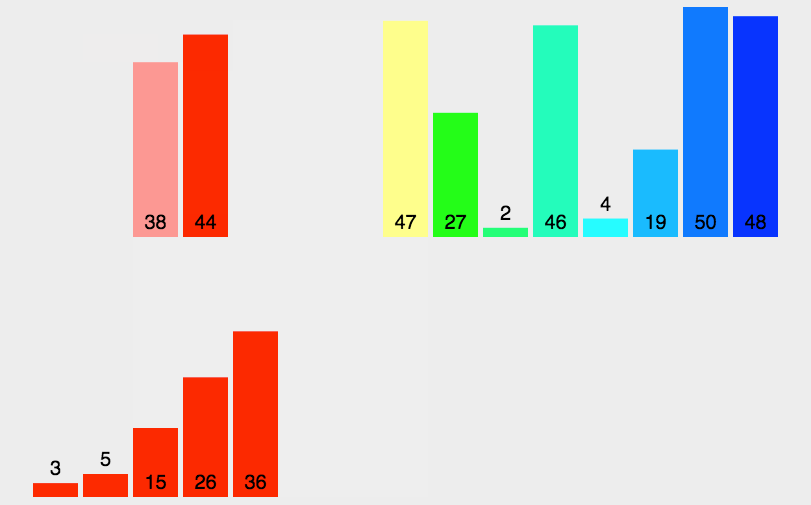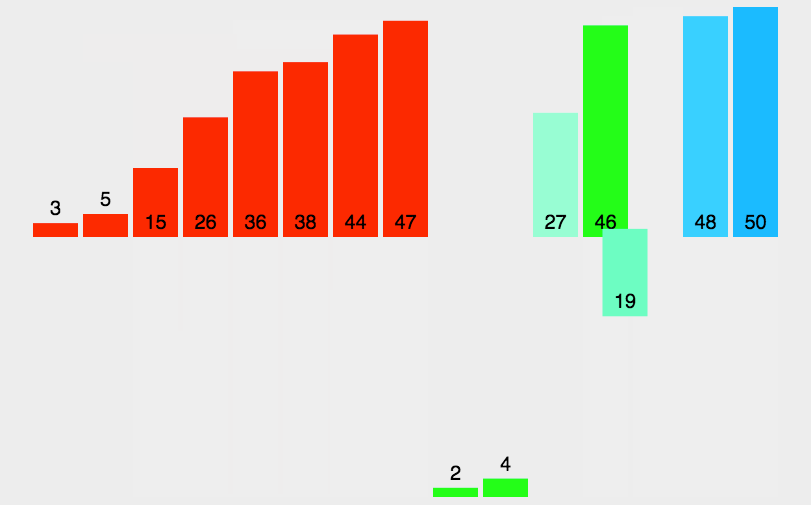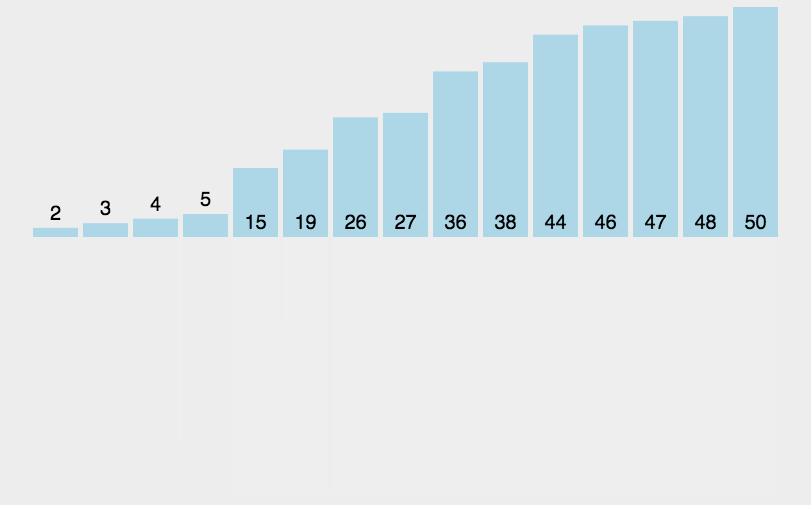
❤分治思想

1. 边界处理
2. 二分，递，即两次调用自己，分别处理左右两部分
3. 归，将左右两部分合并并且排好序

归并排序

上代码：
数组自上而下

import java.util.*;
import java.io.*;
public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));
        int n = sc.nextInt();
        int[] m = new int[n];
        for (int i = 0; i < n; i++) {
            m[i] = sc.nextInt();
        }
        mergeSort(m, 0, n-1);
        for (int i = 0; i < n; i++) {
            System.out.print(m[i] + " ");
        }
    }
    static void mergeSort(int[] m, int l, int r) {
        //边界处理
        if (l >= r) return;
        //一分为二
        int mid = l + (r - l >> 1);
        //递
        mergeSort(m, l, mid);
        mergeSort(m, mid + 1, r);
        //归
        int[] temp = new int[r - l + 1];
        int i = l, j = mid + 1, k = 0;
        while (i <= mid && j <= r) {
            if (m[i] <= m[j]) {
                temp[k++] = m[i++];
            }
            else {
                temp[k++] = m[j++];
            }
        }
        while (i <= mid) temp[k++] = m[i++];
        while (j <= r) temp[k++] = m[j++];
        for (i = l, j = 0; i <= r; i++, j++) {
            m[i] = temp[j];
        }
    }
}

应用

给定一个长度为 nn 的整数数列，请你计算数列中的逆序对的数量。
逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 ia[j]，则其为一个逆序对；否则不是。
输入格式
第一行包含整数 n，表示数列的长度。
第二行包含 n个整数，表示整个数列。
输出格式
输出一个整数，表示逆序对的个数。
数据范围
1≤n≤100000
输入样例：

6
2 3 4 5 6 1

输出样例：

5

上代码：

import java.util.*;
import java.io.*;
public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));
        int n = sc.nextInt();
        int[] q = new int[n];
        for (int i = 0; i < n; i++) {
            q[i] = sc.nextInt();
        }
        long ans = merge(q, 0, n-1);
        System.out.println(ans);
    }
    static long merge(int[] q, int l, int r) {
        if (l >= r) return 0;
        int mid = l + (r - l >> 1);
        long ans = 0;
        ans += merge(q, l, mid) + merge(q, mid + 1, r);
        int[] tmp = new int[r - l + 1];
        int i = l, j = mid + 1, k = 0;
        while (i <= mid && j <= r) {
            if (q[i] <= q[j]) {
                tmp[k++] = q[i++];
            }
            else {
                tmp[k++] = q[j++];
                ans += mid - i + 1;
            }
        }
        while (i <= mid) tmp[k++] = q[i++];
        while (j <= r)   tmp[k++] = q[j++];
        for (i = l, j = 0; i <=r; i++, j++) {
            q[i] = tmp[j];
        }
        return ans;
    }
}

思路：分治的思想