496. 下一个更大元素 I

1475. 商品折扣后的最终价格

739. 每日温度

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1: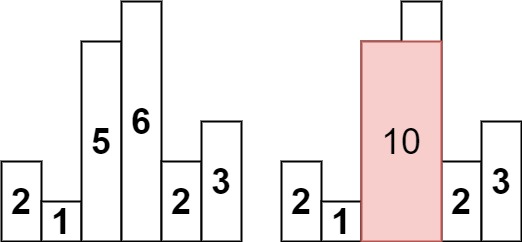
image.png
输入：heights = [2,1,5,6,2,3] 输出：10 解释：最大的矩形为图中红色区域，面积为 10
示例 2：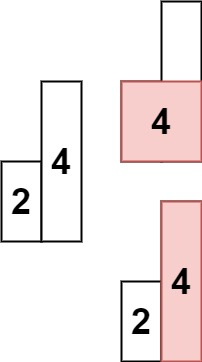
image.png
输入： heights = [2,4] 输出： 4

提示：

  • 1 <= heights.length <=105
  • 0 <= heights[i] <= 104

思路:
用单调递增栈记录还未处理的可能的矩形高度,初始时将-1入栈,方便边界处理
从头到尾遍历数组,记当前遍历的元素下标为i:
比当前高度高的所有元素一次出栈,记出栈元素下标为idx,则idx对应高度的右边界为i,左边界为idx出栈时的当前栈顶元素res = Math.max(res, (i - stack.peek() - 1) * heights[idx])
此时栈顶元素为当前元素所在高度的左边界,将当前元素入栈.
遍历完数组后,栈中剩余元素意为没有右边界,即右边界为n,依次出栈计算每个元素所在高度的最大矩形面积即可.res = Math.max(res, (n - stack.peek() - 1) * height[idx])

  1. class Solution {
  2.     public int largestRectangleArea(int[] heights) {
  3.         int n = heights.length;
  5.         int[] stack = new int[n + 1];
  6.         int p = 0;
  7.         stack[0] = -1;
  9.         int res = 0;
  10.         for (int i = 0; i < n; i++) {
  11.             while (p >= 1 && heights[stack[p]] >= heights[i]) {
  12.                 int idx = stack[p--];
  13.                 res = Math.max(res, (i - stack[p] - 1) * heights[idx]);
  14.             }
  15.             stack[++p] = i;
  16.         }
  17.         while (p >= 1) {
  18.             int idx = stack[p--];
  19.             res = Math.max(res, (n - stack[p] - 1) * heights[idx]);
  20.         }
  21.         return res;
  22.     }
  23. }

一个问题:遍历过程中出栈元素计算矩形面积时,左边界是严格的,右边界并不是,其高度可能等于当前待计算元素高度,如何保证正确性? 若该出栈元素右边界对应的高度等于该元素高度也没关系,正确的高度可以在其右边界处计算得出.

85. 最大矩形

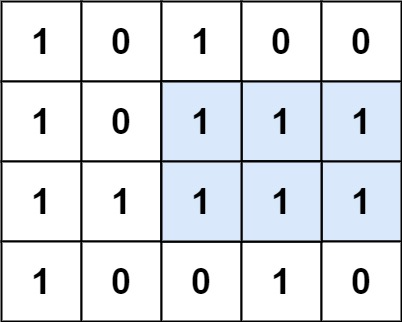
image.png
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：
输入：matrix = [[“1”,”0”,”1”,”0”,”0”],[“1”,”0”,”1”,”1”,”1”],[“1”,”1”,”1”,”1”,”1”],[“1”,”0”,”0”,”1”,”0”]] 输出：6 解释：最大矩形如上图所示。
示例 2：
输入：matrix = [] 输出：0
示例 3：
输入：matrix = [[“0”]] 输出：0
示例 4：
输入：matrix = [[“1”]] 输出：1
示例 5：
输入：matrix = [[“0”,”0”]] 输出：0

提示：

  • rows == matrix.length
  • cols == matrix[0].length
  • 0 <= row, cols <= 200
  • matrix[i][j] 为 '0' 或 '1'

思路:
相较于84,一维变成了二维,得结合一下前缀和,之后逐行按照84的解法计算.

  1. class Solution {
  2.     int ans = 0;
  3.     public int maximalRectangle(char[][] matrix) {
  4.         if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
  5.             return 0;
  6.         int n = matrix.length, m = matrix[0].length;
  8.         int[][] g = new int[n][m];
  9.         for (int i = 0; i < m; i++)
  10.             g[0][i] = matrix[0][i] - '0';
  11.         for (int i = 1; i < n; i++) {
  12.             for (int j = 0; j < m; j++) {
  13.                 if (matrix[i][j] == '1')
  14.                     g[i][j] = g[i - 1][j] + 1;
  15.             }
  16.         }
  17.         for (int[] a : g)
  18.             cal(a);
  19.         return ans;
  20.     }
  21.     void cal(int[] a) {
  22.         int n = a.length;
  23.         int[] right = new int[n], left = new int[n];
  24.         Deque<Integer> stack = new ArrayDeque<>();
  25.         Arrays.fill(right, n);
  26.         for (int i = 0; i < n; i++) {
  27.             while (!stack.isEmpty() && a[stack.peek()] >= a[i]) {
  28.                 right[stack.pop()] = i;
  29.             }
  30.             left[i] = stack.isEmpty() ? -1 : stack.peek();
  31.             stack.push(i);
  32.         }
  33.         for (int i = 0; i < n; i++)
  34.             ans = Math.max(ans, (right[i] - left[i] - 1) * a[i]);
  35.     }
  36. }
  1. // 更巧妙的实现
  2. class Solution {
  3.     int[][] c = new int[201][201];
  4.     int[] l = new int[201], r = new int[201];
  5.     public int maximalRectangle(char[][] a) {
  6.         int n = a.length, m = a[0].length;
  8.         for (int i = 1; i <= n; i++) {
  9.             for (int j = 1; j <= m; j++) {
  10.                 if (a[i - 1][j - 1] == '1')
  11.                     c[i][j] = c[i -  1][j] + 1;
  12.                 else c[i][j] = 0;
  13.             }
  14.         }
  16.         int ans = 0;
  17.         for (int i = 1; i <= n; i++) {
  19.             for (int j = 1; j <= m; j++) {
  20.                 l[j] = j - 1;
  21.                 for (; l[j] > 0 && c[i][j] <= c[i][l[j]]; l[j] = l[l[j]]);
  22.             }
  23.             for (int j = m; j > 0; j--) {
  24.                 r[j] = j + 1;
  25.                 for (; r[j] < m + 1 && c[i][j] <= c[i][r[j]]; r[j] = r[r[j]]);
  26.             }
  27.             for (int j = 1; j <= m; j++) {
  28.                 ans = Math.max(ans, c[i][j] * (r[j] - l[j] - 1));
  29.                 // System.out.println(i + " " + j + " " + " " + c[i][j] + " " + c[i][j] * (r[j] - l[j] - 1));
  30.             }
  31.         }
  32.         return ans;
  33.     }
  34. }

Acwing 3516. 最大面积

究极无敌版求最大矩形面积
题目描述：不是像85一样求二维的最大矩形面积，而是变成了Q个询问，每个询问会讲对应位置1变为0(如果是1的话)，然后问这种情况下的最大矩形面积是多少。
思路：预处理四个数组，上半部分最大面积，下半部分最大面积，左半部分最大面积，右半部分最大面积，这样询问某点删除后的最大面积就是找对应点上下左右部分的最大面积 :::tips 处理左右的时候可以将原矩阵左右反转后做类似的上下操作 :::

456. 132 模式

给你一个整数数组 nums ，数组中共有 n 个整数。132 模式的子序列 由三个整数 nums[i]、nums[j] 和 nums[k] 组成，并同时满足：i < j < k 和 nums[i] < nums[k] < nums[j] 。

如果 nums 中存在 132 模式的子序列 ，返回 true ；否则，返回 false 。

示例 1：
输入：nums = [1,2,3,4]
输出：false
解释：序列中不存在 132 模式的子序列。
示例 2：
输入：nums = [3,1,4,2]
输出：true
解释：序列中有 1 个 132 模式的子序列： [1, 4, 2] 。
示例 3：
输入：nums = [-1,3,2,0]
输出：true
解释：序列中有 3 个 132 模式的的子序列：[-1, 3, 2]、[-1, 3, 0] 和 [-1, 2, 0] 。

提示：
n == nums.length
1 <= n <= 2 * 105
-109 <= nums[i] <= 109

这个单调栈有点难度的！！！
思路：
对于每个ai，判断其后是否存在一个满足要求的ak
使得ak > ai且在i与k之间存在j满足aj > ak
如何用单调栈？
对于132模式中的32使用单调栈来维护，倒着遍历数组维护一个单调递减栈
遍历到当前元素x时，所有栈中比x小的数会被弹出，且被弹出的数满足32模式，故只需用一个变量max维护最大的满足32模式的ak即可，这样在向前遍历时，如果该数x < max 说明存在完整的132模式，返回true即可。

从左到右枚举 1 的下标 i，那么 j,k 的下标范围都是减少的，这样就不利于对它们进行维护。因此我们可以考虑从右到左枚举 i。 如果存在 (j,k) 满足要求的话，我们只需要找到一个最大的满足条件的 k，通过与 i 的比较即可。

:::tips 核心在于132模式中32是连续的，所以好维护 :::

  1. class Solution {
  2.     public boolean find132pattern(int[] nums) {
  3.         int max = Integer.MIN_VALUE;
  4.         int n = nums.length;
  5.         int[] stk = new int[n + 1];
  6.         int p = -1;
  7.         for (int i = n - 1; i >= 0; i--) {
  8.             if (nums[i] < max) return true;
  9.             while (p > -1 && nums[i] > stk[p]) {
  10.                 max = Math.max(max, stk[p--]);
  11.             }
  12.             stk[++p] = nums[i];
  13.         }
  14.         return false;
  15.     }
  16. }

2104. 子数组范围和

思路：见链接跳转
类似的题目还有：
907. 子数组的最小值之和
795. 区间子数组个数

6080. 使数组按非递减顺序排列

单调栈+ DP
思路：见链接跳转