
虽然排名不高,但考虑到t3和t4都是原题,而我都是现场做的,且没有wrong,就没那么难受了
6148. 矩阵中的局部最大值
给你一个大小为 n x n 的整数矩阵 grid 。
生成一个大小为 (n - 2) x (n - 2) 的整数矩阵 maxLocal ,并满足:
- maxLocal[i][j] 等于 grid 中以 i + 1 行和 j + 1 列为中心的 3 x 3 矩阵中的 最大值 。
换句话说,我们希望找出 grid 中每个 3 x 3 矩阵中的最大值。
返回生成的矩阵。
示例 1: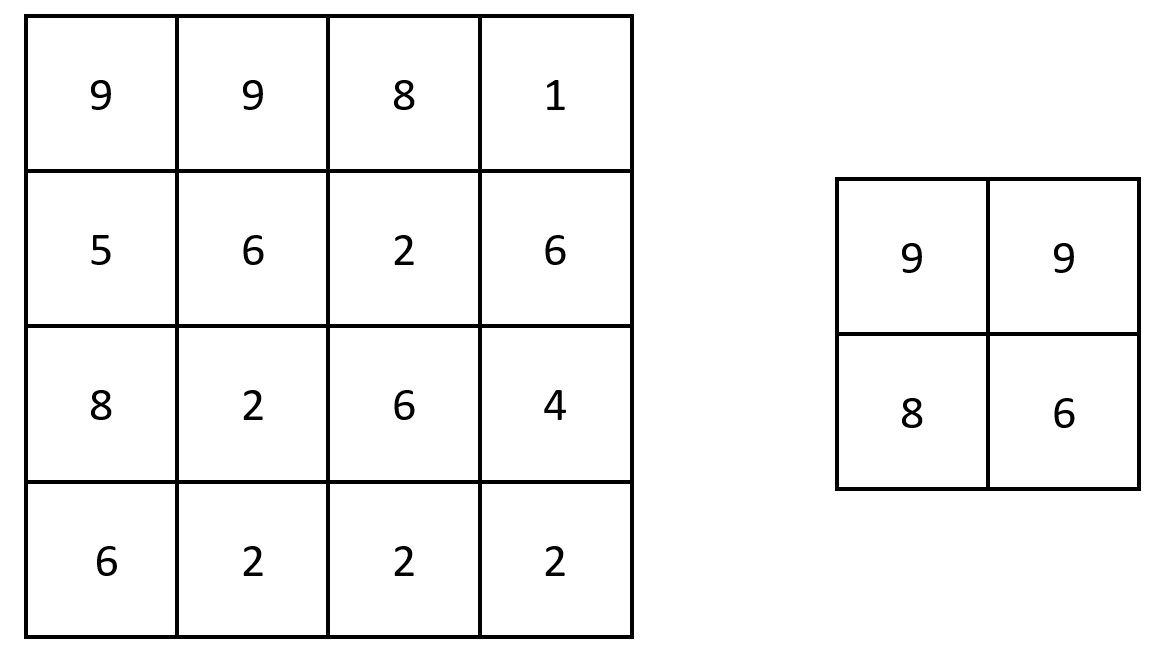
输入:grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]] 输出:[[9,9],[8,6]] 解释:原矩阵和生成的矩阵如上图所示。 注意,生成的矩阵中,每个值都对应 grid 中一个相接的 3 x 3 矩阵的最大值。
示例 2: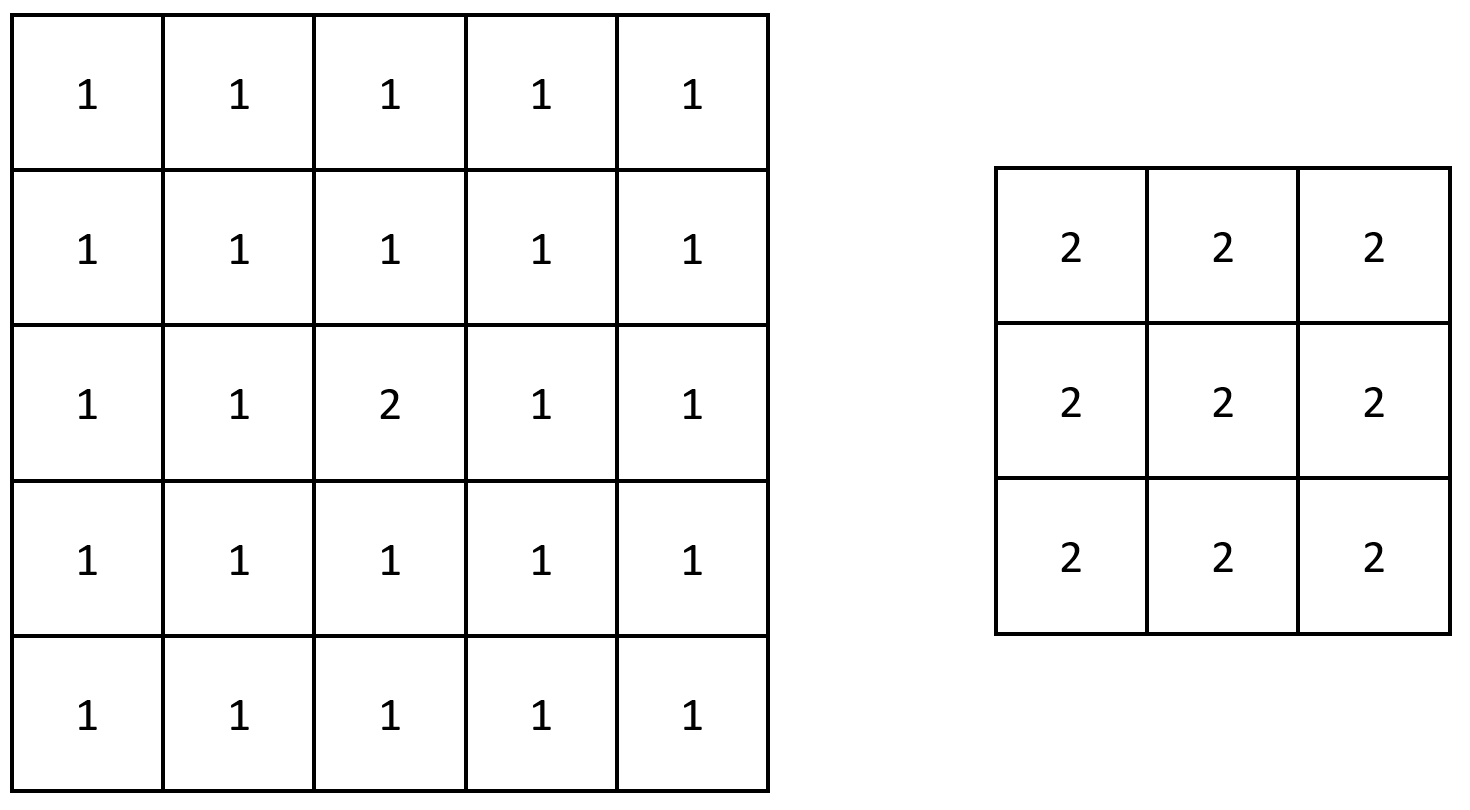
输入:grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]] 输出:[[2,2,2],[2,2,2],[2,2,2]] 解释:注意,2 包含在 grid 中每个 3 x 3 的矩阵中。
提示:
- n == grid.length == grid[i].length
- 3 <= n <= 100
- 1 <= grid[i][j] <= 100
思路:
暴力枚举即可
class Solution {public int[][] largestLocal(int[][] g) {int n = g.length;int[][] res = new int[n - 2][n - 2];for (int i = 0; i < n - 2; i++) {for (int j = 0; j < n - 2; j++) {int max = 0;for (int l = i; l <= i + 2; l++) {for (int r = j; r <= j + 2; r++) {max = Math.max(max, g[l][r]);}}res[i][j] = max;}}return res;}}
进阶问题:如果不是求33矩阵的最大值,而是hw怎么办?
答:用单调队列优化,先行再列
Acwing 1091. 理想的正方形
6149. 边积分最高的节点
- 通过的用户数4810
- 尝试过的用户数5430
- 用户总通过次数4868
- 用户总提交次数12955
- 题目难度Medium
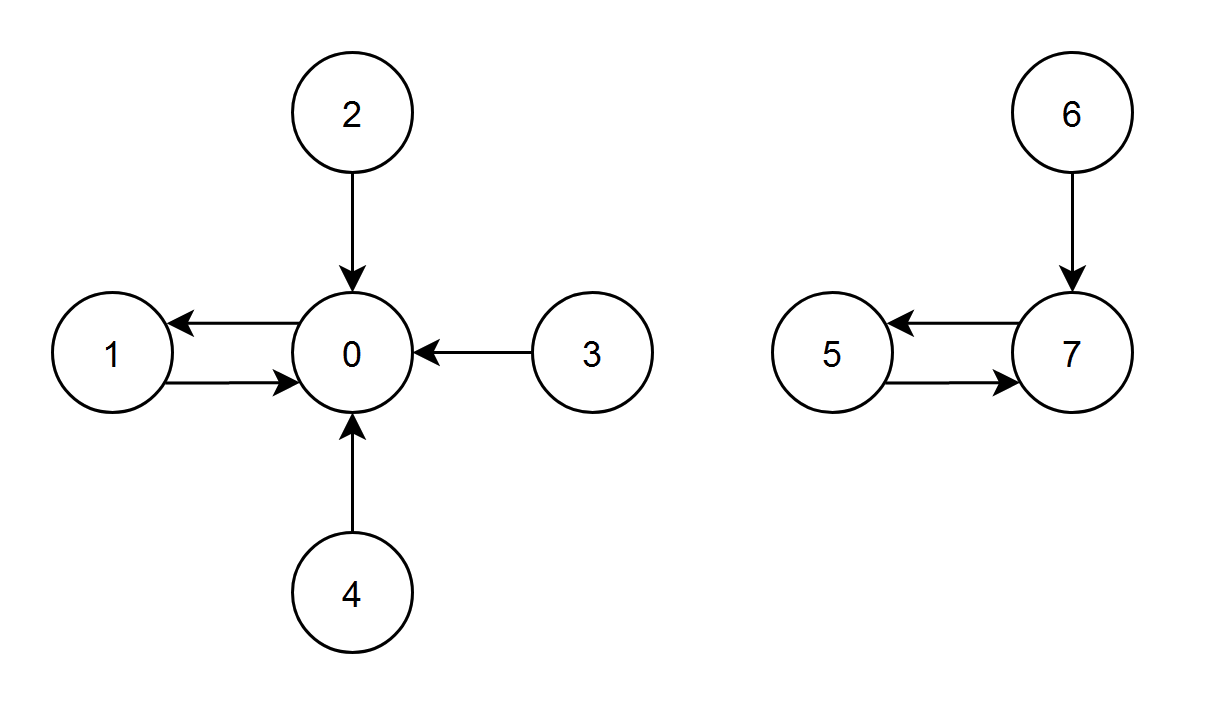
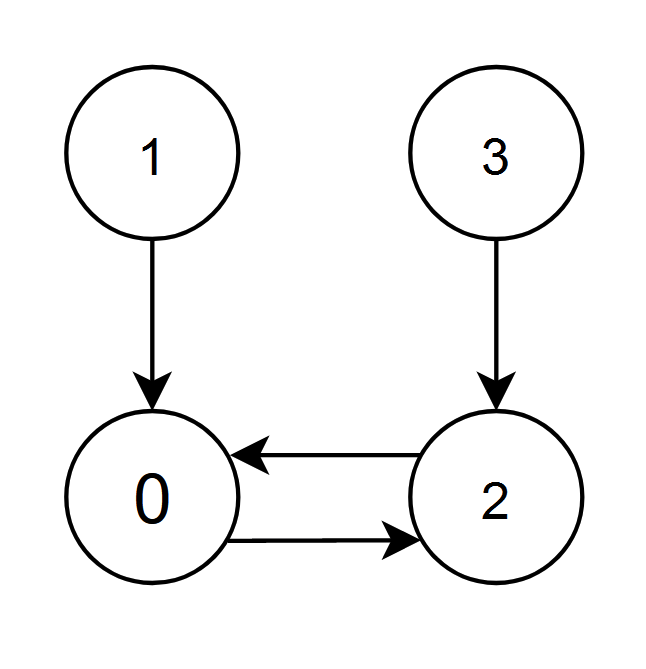
给你一个有向图,图中有 n 个节点,节点编号从 0 到 n - 1 ,其中每个节点都 恰有一条 出边。
图由一个下标从 0 开始、长度为 n 的整数数组 edges 表示,其中 edges[i] 表示存在一条从节点 i 到节点 edges[i] 的 有向 边。
节点 i 的 边积分 定义为:所有存在一条指向节点 i 的边的节点的 编号 总和。
返回 边积分 最高的节点。如果多个节点的 边积分 相同,返回编号 最小 的那个。
示例 1:
输入:edges = [1,0,0,0,0,7,7,5] 输出:7 解释: - 节点 1、2、3 和 4 都有指向节点 0 的边,节点 0 的边积分等于 1 + 2 + 3 + 4 = 10 。 - 节点 0 有一条指向节点 1 的边,节点 1 的边积分等于 0 。 - 节点 7 有一条指向节点 5 的边,节点 5 的边积分等于 7 。 - 节点 5 和 6 都有指向节点 7 的边,节点 7 的边积分等于 5 + 6 = 11 。 节点 7 的边积分最高,所以返回 7 。
示例 2:
输入:edges = [2,0,0,2] 输出:0 解释: - 节点 1 和 2 都有指向节点 0 的边,节点 0 的边积分等于 1 + 2 = 3 。 - 节点 0 和 3 都有指向节点 2 的边,节点 2 的边积分等于 0 + 3 = 3 。 节点 0 和 2 的边积分都是 3 。由于节点 0 的编号更小,返回 0 。
提示:
- n == edges.length
- 2 <= n <= 105
- 0 <= edges[i] < n
- edges[i] != i
思路:
统计每个节点的入边权值和,找最大且编号最小的点即可
class Solution {public int edgeScore(int[] e) {int n = e.length;long[] c = new long[n];for (int i = 0; i < n; i++) {c[e[i]] += i;}int max = 0;for (int i = 0; i < n; i++) {if (c[i] > c[max])max = i;}return max;}}
6150. 根据模式串构造最小数字
- 通过的用户数3131
- 尝试过的用户数3555
- 用户总通过次数3261
- 用户总提交次数5251
- 题目难度Medium
给你下标从 0 开始、长度为 n 的字符串 pattern ,它包含两种字符,’I’ 表示 上升 ,’D’ 表示 下降 。
你需要构造一个下标从 0 开始长度为 n + 1 的字符串,且它要满足以下条件:
- num 包含数字 ‘1’ 到 ‘9’ ,其中每个数字 至多 使用一次。
- 如果 pattern[i] == ‘I’ ,那么 num[i] < num[i + 1] 。
- 如果 pattern[i] == ‘D’ ,那么 num[i] > num[i + 1] 。
请你返回满足上述条件字典序 最小 的字符串_ _num。
示例 1:
输入:pattern = “IIIDIDDD” 输出:“123549876” 解释: 下标 0 ,1 ,2 和 4 处,我们需要使 num[i] < num[i+1] 。 下标 3 ,5 ,6 和 7 处,我们需要使 num[i] > num[i+1] 。 一些可能的 num 的值为 “245639871” ,”135749862” 和 “123849765” 。 “123549876” 是满足条件最小的数字。 注意,”123414321” 不是可行解因为数字 ‘1’ 使用次数超过 1 次。
示例 2:
输入:pattern = “DDD” 输出:“4321” 解释: 一些可能的 num 的值为 “9876” ,”7321” 和 “8742” 。 “4321” 是满足条件最小的数字。
提示:
- 1 <= pattern.length <= 8
- pattern 只包含字符 ‘I’ 和 ‘D’ 。
思路:
方法1:看到数据比较小,直接爆搜
// 赛时代码class Solution {String p;int n;int[] path = new int[10];boolean[] st = new boolean[10];String res = null;public String smallestNumber(String pattern) {p = pattern;n = p.length() + 1;dfs(0);return res;}boolean dfs(int u) {if (u == n) {if (check()) {StringBuilder sb = new StringBuilder();for (int i = 0; i < n; i++)sb.append(path[i]);res = sb.toString();return true;}return false;}for (int i = 1; i <= 9; i ++) {if (st[i]) continue;st[i] = true;path[u] = i;if (dfs(u + 1)) return true;st[i] = false;}return false;}boolean check() {for (int i = 0; i < n - 1; i++) {char c = p.charAt(i);if (c == 'I') {if (path[i + 1] < path[i]) return false;} else {if (path[i + 1] > path[i]) return false;}}return true;}}// 优化一下,不是最后check,而是边填边checkclass Solution {String res = null;int n;String p;public String smallestNumber(String pattern) {this.n = pattern.length();this.p = pattern;for (int i = 1; i <= n + 1; i++) {if (dfs(0, i, 1 << i, i))break;}return res;}boolean dfs(int u, int pre, int st, int x) {if (u == n) {res = x + "";return true;}char c = p.charAt(u);for (int i = 1; i <= n + 1; i++) {if ((st >> i & 1) == 1) continue;if (c == 'I' && i < pre) continue;if (c == 'D' && i > pre) continue;if (dfs(u + 1, i, st | 1 << i, x * 10 + i)) return true;}return false;}}
方法2:用栈构造
先考虑最特殊的情况III...III全为I
再考虑中间有D怎么办
例IIIII = 1 2 3 4 5
IIDII= 1 2 4 3 5
class Solution {public String smallestNumber(String p) {int n = p.length();char[] a = new char[n + 1];int idx = 0;Deque<Character> stk = new ArrayDeque<>();for (int i = 1; i <= n; i++) {if (p.charAt(i - 1) == 'I') {stk.push((char)(i + '0'));while (!stk.isEmpty())a[idx++] = stk.pop();} else {stk.push((char)(i + '0'));}}stk.push((char)(n + 1 + '0'));while (!stk.isEmpty())a[idx++] = stk.pop();return new String(a);}}
原题:Leetcode 484. 寻找排列
扩展:903. DI 序列的有效排列
6151. 统计特殊整数
如果一个正整数每一个数位都是 互不相同 的,我们称它是 特殊整数 。
给你一个 正 整数 n ,请你返回区间 [1, n] 之间特殊整数的数目。
示例 1:
输入:n = 20 输出:19 解释:1 到 20 之间所有整数除了 11 以外都是特殊整数。所以总共有 19 个特殊整数。
示例 2:
输入:n = 5 输出:5 解释:1 到 5 所有整数都是特殊整数。
示例 3:
输入:n = 135 输出:110 解释:从 1 到 135 总共有 110 个整数是特殊整数。 不特殊的部分数字为:22 ,114 和 131 。
提示:
- 1 <= n <= 2 * 109
思路:方法1:数位DP
class Solution {public int countSpecialNumbers(int n) {if (n <= 10) return n;boolean[] st = new boolean[10];String num = Integer.toString(n);n = num.length();int res = 0;for (int i = 0; i < n; i++) {int x = num.charAt(i) - '0';int c = 0;for (int j = 0; j < x; j++)if (!st[j]) c++;if (i == 0) {// 0for (int j = 0; j < n - 1; j++) {res += 9 * A(9, j);}// 非0c--;if (c >= 0)res += c * A(9, n - 1);} else {res += c * A(10 - (i + 1), n - 1 - i);}if (st[x]) break;st[x] = true;if (i == n - 1){res++;break;}}return res;}int A(int x, int y) {int res = 1;for (int i = y; i > 0; i--)res *= x--;return res;}}
// 记忆化搜索class Solution {int[][] f = new int[10][1 << 10];List<Integer> num = new ArrayList<>();public int countSpecialNumbers(int n) {while (n > 0) {num.add(n % 10);n /= 10;}for (int i = 0; i < 10; i++)Arrays.fill(f[i], -1);return dfs(num.size() - 1, 1, 1, 0);}int dfs(int cur, int lim, int lead, int mask) {if (cur == -1)return lead == 0 ? 1 : 0;int ans = f[cur][mask];if (lim != 1 && lead != 1 && ans >= 0) return ans;ans = 0;if (lead == 1) ans += dfs(cur - 1, 0, 1, mask);for (int x = lead == 1 ? 1 : 0; x <= (lim == 1 ? num.get(cur) : 9); x++) {if ((mask >> x & 1) == 1) continue;if (lim == 1 && x == num.get(cur))ans += dfs(cur - 1, 1, 0, mask | (1 << x));elseans += dfs(cur - 1, 0, 0, mask | (1 << x));}if (lead != 1 && lim != 1) f[cur][mask] = ans;return ans;}}
方法2:爆搜
需要加点技巧(lowbit),减少无效枚举
class Solution {int[] a = new int[1024];int n;int res;public int countSpecialNumbers(int n) {this.n = n;for (int i = 0; i < 10; i++)a[1 << i] = i;for (int i = 1; i < 10; i++) {dfs(i, 1023 - (1 << i));}return res;}void dfs(long x, int st) {if (x > n) return;res++;int cur = 0;while (st > 0) {int v = st & (-st);st -= v;dfs(x * 10 + a[v], st + cur);cur += v;}}}

