前缀和

什么是前缀和？

给定一个元素个数为n的数组A，数组元素为a1``, a2``, ... , an。
前缀和是这样一个数组，其元素满足
s1 = a1
s2 = a1 + a2
s3 = a1 + a2 + a3
...
sn = a1 + a2 + ... + an
也就是说
s1 = s0+a1
s2 = s1 + a2
s3 = s2 + a3
...
sn = s(n-1) + an

注意：为了避免下标的转换，使原数组A下标从1开始计数。

前缀和的用处

给定原数组A，求A的某一段序列的和。

注意：两种给定序列区间的说法：

  • 起始下标i和结束下标j（都是闭区间）
  • 求数组A中第l个元素至第r个元素的和（闭区间）

我们的前缀和数组直接对应第二种说法：result = s[r] - s[l-1]
如果是第一种说法，需要转换成第二种，方便理解。即l = i + 1, r = j + 1; result = s[r] - s[l-1]

一维数组前缀和

例题：

Acwing 795. 前缀和 数组 前缀和

输入一个长度为 n 的整数序列。
接下来再输入 m 个询问，每个询问输入一对 l,r。
对于每个询问，输出原序列中从第 l 个数到第 r 个数的和。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数，表示整数数列。
接下来 m行，每行包含两个整数 l 和 r，表示一个询问的区间范围。
输出格式
共 m 行，每行输出一个询问的结果。
数据范围
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000
输入样例：

  1. 5 3
  2. 2 1 3 6 4
  3. 1 2
  4. 1 3
  5. 2 4

输出样例：

  1. 3
  2. 6
  3. 10
  1. import java.util.*;
  3. public class Main {
  4.     static final int N = 100010;
  5.     static int[] pre = new int[N];
  6.     static int n, m;
  7.     public static void main(String[] args) {
  8.         Scanner sc = new Scanner(System.in);
  9.         n = sc.nextInt();
  10.         m = sc.nextInt();
  12.         for (int i = 1; i <= n; i++) {
  13.             pre[i] = sc.nextInt();
  14.             pre[i] += pre[i - 1];
  15.         }
  17.         while (m-- > 0) {
  18.             int l = sc.nextInt(), r = sc.nextInt();
  19.             int res = query(l, r);
  20.             System.out.println(res);
  21.         }
  22.     }
  24.     static int query(int l, int r) {
  25.         return pre[r] - pre[l - 1];
  26.     }
  27. }

二维数组前缀和

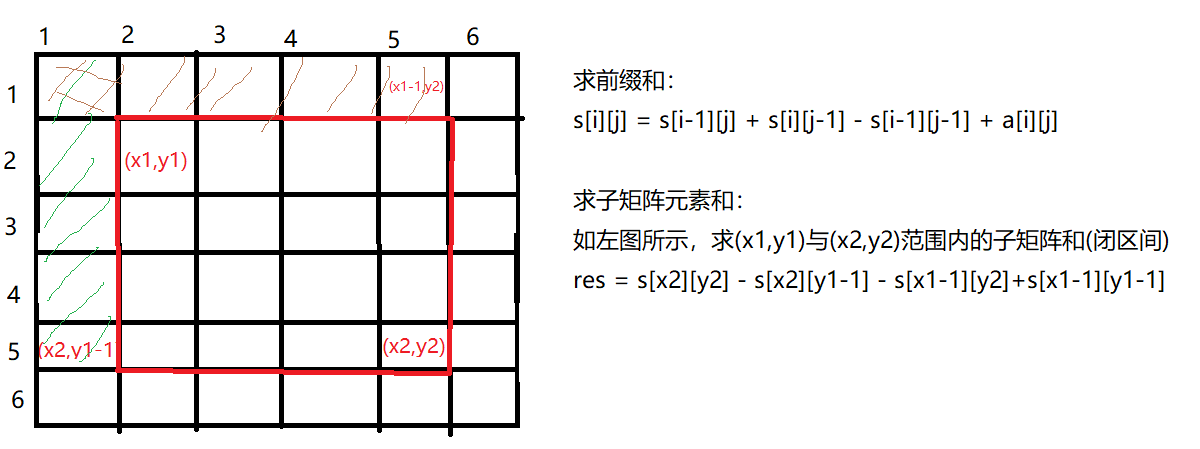
image.png
例题：

AcWing 796. 子矩阵的和 数组 前缀和

输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数 n，m，q。
接下来 n 行，每行包含 m 个整数，表示整数矩阵。
接下来 q 行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。
输出格式
共 q 行，每行输出一个询问的结果。
数据范围
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000
输入样例：

  1. 3 4 3
  2. 1 7 2 4
  3. 3 6 2 8
  4. 2 1 2 3
  5. 1 1 2 2
  6. 2 1 3 4
  7. 1 3 3 4

输出样例：

  1. 17
  2. 27
  3. 21
  1. import java.util.*;
  3. public class Main {
  4.     static final int N = 1010;
  5.     static int[][] pre = new int[N][N];
  6.     static int n, m, q;
  7.     public static void main(String[] args) {
  8.         Scanner sc = new Scanner(System.in);
  9.         n = sc.nextInt();
  10.         m = sc.nextInt();
  11.         q = sc.nextInt();
  13.         for (int i = 1; i <= n; i++) {
  14.             for (int j = 1; j <= m; j++) {
  15.                 int x = sc.nextInt();
  16.                 pre[i][j] = x + pre[i - 1][j] + pre[i][j - 1] - pre[i - 1][j - 1];
  17.             }
  18.         }
  19.         while (q-- > 0) {
  20.             int x1 = sc.nextInt(), y1 = sc.nextInt();
  21.             int x2 = sc.nextInt(), y2 = sc.nextInt();
  22.             int res = query(x1, y1, x2, y2);
  23.             System.out.println(res);
  24.         }
  25.     }
  27.     static int query(int x1, int y1, int x2, int y2) {
  28.         return pre[x2][y2] - pre[x2][y1 - 1] - pre[x1 - 1][y2] + pre[x1 - 1][y1 - 1];
  29.     }
  30. }

差分

什么是差分？

差分是前缀和的逆运算，对于数组a和b来说，假设a是原数组，b是a数组的差分数组，那么对于b来说，a数组就是b数组的前缀和数组。
如果定义前缀和为函数f，有a = f(b), b = f``-1``(a)

差分的用处

如果想对数组a的一个子序列进行整体操作，使得该子序列的每个元素都+c，如果不用差分来做，每次操作时间复杂度都为O(n)，而使用差分数组b来做，只需要一次初始化O(n)操作，其它对子序列的整体操作时间复杂度都为O(1)
拥有数组b[n]后，想要对a数组中所有的数据加上c,只需要将b[1]+c即可，因为a[i]是b[i]的前缀和，a[i]=b[1]+b[1]+b[3]+……+b[n]。
如果想将a数组中[l,r]部分的数据全部加上c，只需要将b[l]+c,然后b[r+1]-c即可。

差分数组的构造也可以使用上述思想，即[l, r] 变成[i,i]即可。

注意：同前缀和一样，数组都是从1开始的，如果原数组的个数为n，那么差分数组的长度为n+2,这样做的好处是方便边界处理（前后各一个）。

一维差分

Acwing 797. 差分 数组 差分

输入一个长度为n的整数序列。
接下来输入m个操作，每个操作包含三个整数l, r, c，表示将序列中[l, r]之间的每个数加上c。
请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数n和m。
第二行包含n个整数，表示整数序列。
接下来m行，每行包含三个整数l，r，c，表示一个操作。

输出格式
共一行，包含n个整数，表示最终序列。
数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例：

  1. 6 3
  2. 1 2 2 1 2 1
  3. 1 3 1
  4. 3 5 1
  5. 1 6 1

输出样例：

  1. 3 4 5 3 4 2
  1. import java.util.*;
  3. public class Main {
  4.     static final int N = 100010;
  5.     static int[] diff = new int[N];
  6.     static int n, m;
  8.     public static void main(String[] args) {
  9.         Scanner sc = new Scanner(System.in);
  10.         n = sc.nextInt();
  11.         m = sc.nextInt();
  13.         for (int i = 1; i <= n; i++) {
  14.             int x = sc.nextInt();
  15.             update(i, i, x);
  16.         }
  18.         for (int i = 0; i < m; i++) {
  19.             int l = sc.nextInt(), r = sc.nextInt(), x = sc.nextInt();
  20.             update(l, r, x);
  21.         }
  23.         for (int i = 1; i <= n; i++)
  24.             diff[i] += diff[i - 1];
  25.         for (int i = 1; i <= n; i++)
  26.             System.out.print(diff[i] + " ");
  28.     }
  30.     static void update(int l, int r, int x) {
  31.         diff[l] += x;
  32.         diff[r + 1] -= x;
  33.     }
  34. }

二维差分

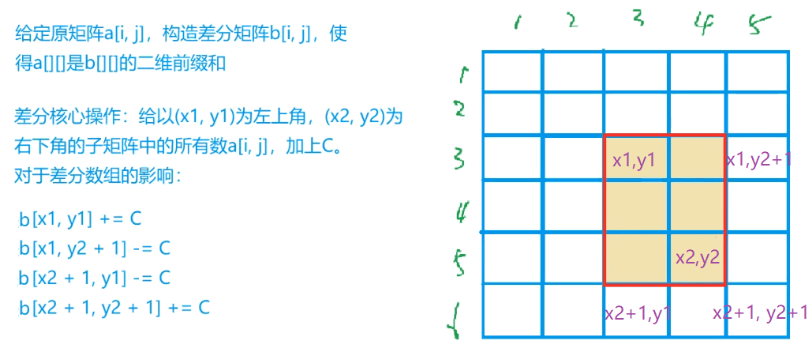
前缀和与差分 - 图2
例题：

Acwing 798. 差分矩阵 数组 差分

输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数x1, y1, x2, y2, c，其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上c。
请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数n,m,q。
接下来n行，每行包含m个整数，表示整数矩阵。
接下来q行，每行包含5个整数x1, y1, x2, y2, c，表示一个操作。

输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000

输入样例：

  1. 3 4 3
  2. 1 2 2 1
  3. 3 2 2 1
  4. 1 1 1 1
  5. 1 1 2 2 1
  6. 1 3 2 3 2
  7. 3 1 3 4 1

输出样例：

  1. 2 3 4 1
  2. 4 3 4 1
  3. 2 2 2 2
  1. import java.util.*;
  2. import java.io.*;
  4. public class Main {
  5.     static final int N = 1010;
  6.     static int[][] a = new int[N][N];
  7.     static int n, m, q;
  8.     public static void main(String[] args) throws IOException {
  9.         BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
  10.         BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
  11.         String[] ss = br.readLine().split(" ");
  12.         n = Integer.parseInt(ss[0]);
  13.         m = Integer.parseInt(ss[1]);
  14.         q = Integer.parseInt(ss[2]);
  15.         for (int i = 1; i <= n; i++) {
  16.             ss = br.readLine().split(" ");
  17.             for (int j = 1; j <= m; j++) {
  18.                 int x = Integer.parseInt(ss[j - 1]);
  19.                 add(i, j, i, j, x);
  20.             }
  21.         }
  22.         while (q-- > 0) {
  23.             ss = br.readLine().split(" ");
  24.             int x1 = Integer.parseInt(ss[0]), y1 = Integer.parseInt(ss[1]);
  25.             int x2 = Integer.parseInt(ss[2]), y2 = Integer.parseInt(ss[3]);
  26.             int v = Integer.parseInt(ss[4]);
  27.             add(x1, y1, x2, y2, v);
  28.         }
  30.         for (int i = 1; i <= n; i++) {
  31.             for (int j = 1; j <= m; j++) {
  32.                 a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
  33.                 bw.write(a[i][j] + " ");
  34.             }
  35.             bw.write("\n");
  36.         }
  37.         bw.close();
  38.         br.close();
  39.     }
  41.     static void add(int x1, int y1, int x2, int y2, int c) {
  42.         a[x1][y1] += c;
  43.         a[x1][y2 + 1] -= c;
  44.         a[x2 + 1][y1] -= c;
  45.         a[x2 + 1][y2 + 1] += c;
  46.     }
  47. }

三维差分

其它例题

798. 得分最高的最小轮调

798 得分最高的最小轮调.pdf

  1. class Solution {
  2.     public int bestRotation(int[] nums) {
  3.         int n = nums.length;
  5.         int[] diff = new int[n + 1];
  6.         for (int i = 0; i < n; i++) {
  7.             if (nums[i] <= i) { // 第一类
  8.                 diff[0] += 1;
  9.                 diff[i - nums[i] + 1] -= 1;
  10.                 diff[i + 1] += 1;
  11.             } else { //第二类
  12.                 diff[0] += 0;
  13.                 diff[i + 1] += 1;
  14.                 diff[i + 1 + n - nums[i]] -= 1;
  15.             }
  16.         }
  18.         int minIdx = 0, score = 0;
  19.         int sum = 0;
  20.         for (int i = 0; i < n; i++) {
  21.             sum += diff[i];
  22.             if (sum > score) {
  23.                 score = sum;
  24.                 minIdx = i;
  25.             }
  26.         }
  27.         return minIdx;
  28.     }
  29. }