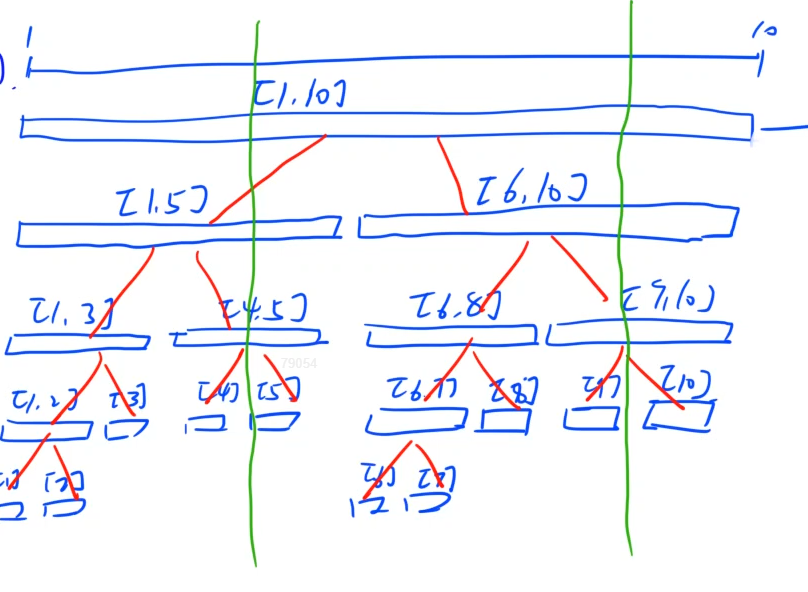
线段树概述：

  • 每个节点表示一段区间
  • 具有唯一根节点，表示整个统计范围
  • 每个叶节点代表一个长度为1的元区间

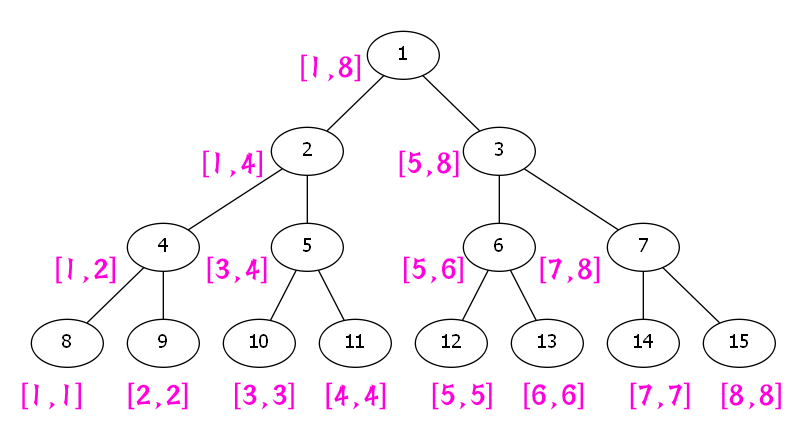
image.png

image.png

基本操作

  1. pushup(int u)

由子节点算父节点信息，例如sum = l.sum + r.sum

  1. build() 将一段区间初始化为线段树

用一维数组存储整棵树，类似于堆。
编号为x的节点

  1.   - 父节点 `x / 2`或 `x >> 1`
  2.   - 左儿子 `2x` 或 `x << 1`
  3.   - 右儿子 `2x` 或 `x << 1 | 1`
  1. modify()
    1. 修改一个点
    2. 修改一段区间 pushdown() ，即懒标记/延迟标记。

将父节点的信息更新到子节点

  1. query() 查询某一段区间的信息
  2. pushdown()操作

灵感来自于query操作，新增add字段作为懒标记
给以当前节点为根的子树中的每一个节点加上add（不包含根节点）
相应的，使用懒标记后查询操作也得发生变化，先pushdown再query，修改操作先pushdown再modify
一个疑问：为什么modify的时候也需要先pushdown？ 如果被打上懒标记的区间的一个子区间被修改，势必会执行pushup操作，而根区间由于懒标记并未向下传递会导致子区间在原来的数值上修改并影响了跟区间，从而导致懒标记毫无作用。

  1. //初始化
  2. N = <输入规模>
  3. Node[] tr = new Node[4 * N];
  4. build(int u, int l, int r) {
  5.      tr[u] = new Node(l, r);
  6.     if (l == r) {
  7.          对tr[u]的其它属性进行赋值操作   
  8.     }
  9.        int mid = l + r >> 1;
  10.     build(u << 1, l, mid);
  11.     build(u << 1 | 1, mid, r);
  12.     pushup(u);
  13. }
  15. //pushup
  16. 这个操作时间复杂度一般为O(1)
  17. 应用在递归回退的过程中用子节点更新父节点
  19. //查询
  20. /*
  21.     待查询区间为[l, r], 当前线段树节点区间为[Tl, Tr]
  22.     ①：[Tl, Tr] ∈[l, r] 直接返回
  23.     ②：[Tl, Tr] ∩ [l, r] != 空     //一定成立，因为不会遍历那些没有交集的节点
  24.     时间复杂度约为4lgn，n指待查询区间(r - l + 1)
  25. */
  27. //单点修改
  28. 只需要从上往下递归遍历某一分支，时间复杂度为O(lgn)

原理

整棵线段树是一棵二叉树，并且除了最后一层，是一个满二叉树。
树的深度为O(logN)，可以用类似堆的方法，用数组存储线段树。
分界点取法：
mid = l + r >> 1 左半： [l, mid] 右半： [mid + 1, r]
编号为x，父节点为 x >> 1 ，左儿子为 x << 1 ，右儿子为 x << 1 | 1
存储空间开多大？
4 * n
4N 即全树节点数估计，区间长度为N的线段树，理想情况下N个叶节点的满二叉树有N + N / 2 + N / 4 + ... + 1 = 2N - 1个节点。使用数组存储时最后一层会有空余，所以保存线段树的数组长度要不小于4N保证不会越界。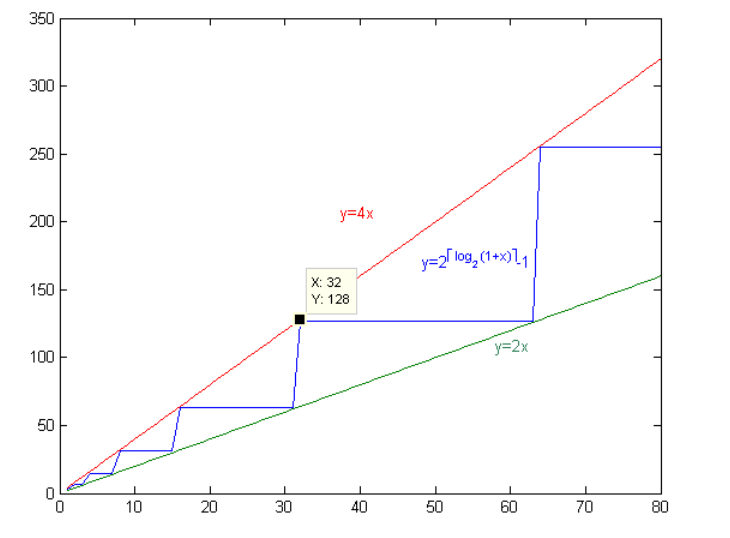
image.png

问题类型

  1. 单点修改，区间查询

Acwing 1275. 最大数

  1. 维护懒标记，区间修改，区间查询

AcWing 243. 一个简单的整数问题2
AcWing 1277. 维护序列

  1. 扫描线

AcWing 247. 亚特兰蒂斯

【hdu1542】线段树求矩形面积并

  1. 动态开点线段树

715. Range 模块

699. 掉落的方块
注意本题有点坑：某段区间变高是在添加之前的最高一段区间的基础上加的

方法1：面向对象动态开点

  1. class Solution {
  2.     public List<Integer> fallingSquares(int[][] positions) {
  3.         Node root = new Node(1, (int)(1e9));
  5.         List<Integer> res = new ArrayList<>();
  6.         for (int[] p : positions) {
  7.             int h = root.query(p[0], p[0] + p[1] - 1);
  8.             root.modify(p[0], p[0] + p[1] - 1, p[1] + h);
  9.             res.add(root.height);
  10.         }
  11.         return res;
  12.     }
  13. }
  15. class Node {
  16.     int l, r;
  17.     int height, add;
  18.     Node left, right;
  20.     Node(int l, int r) {
  21.         this.l = l;
  22.         this.r = r;
  23.     }
  25.     int query(int l, int r) {
  26.         if (l <= this.l && r >= this.r)
  27.             return height;
  28.         else {
  29.             int mid = this.l + this.r >> 1;
  30.             if (this.left == null) {
  31.                 this.left = new Node(this.l, mid);
  32.             }
  33.             if (this.right == null) {
  34.                 this.right = new Node(mid + 1, this.r);
  35.             }
  36.             pushdown();
  37.             int res = 0;
  38.             if (l <= mid) res = left.query(l, r);
  39.             if (r > mid) res = Math.max(res, right.query(l, r));
  40.             return res; 
  41.         }
  42.     }
  44.     void modify(int l, int r, int x) {
  45.         if (l <= this.l && r >= this.r) {
  46.             this.height = x;
  47.             this.add = x;
  48.         } else {
  49.             int mid = this.l + this.r >> 1;
  50.             if (this.left == null) {
  51.                 this.left = new Node(this.l, mid);
  52.             }
  53.             if (this.right == null) {
  54.                 this.right = new Node(mid + 1, this.r);
  55.             }
  56.             pushdown();
  57.             if (l <= mid) this.left.modify(l, r, x);
  58.             if (r > mid) this.right.modify(l, r, x);
  59.             pushup();
  60.         }
  61.     }
  63.     void pushup() {
  64.         height = Math.max(right.height, left.height);
  65.     }
  67.     void pushdown() {
  68.         if (add > 0) {
  69.             left.height = add;
  70.             left.add = add;
  71.             right.height = add;
  72.             right.add = add;
  73.             add = 0;
  74.         }
  75.     }
  76. }

方法2：面向过程动态开点
预估节点数为查询次数 6 log(n)，n为总区间大小

  1. class Solution {
  2.     class Node {
  3.         int idxl, idxr;
  4.         int height;
  5.         int add;
  6.     }
  7.     Node[] tr = new Node[240010];
  8.     int idx = 1;
  9.     public List<Integer> fallingSquares(int[][] positions) {
  10.         List<Integer> res = new ArrayList<>();
  11.         for (int[] p : positions) {
  12.             int h = query(1, 1, (int)(1e9), p[0], p[1] + p[0] - 1);
  13.             modify(1, 1, (int)(1e9), p[0], p[0] + p[1] - 1, p[1] + h);
  14.             res.add(tr[1].height);
  15.         }
  16.         return res;
  17.     }
  19.     void modify(int u, int l, int r, int ql, int qr, int x) {
  20.         if (ql <= l && qr >= r) {
  21.             tr[u].height = x;
  22.             tr[u].add = x;
  23.         } else {
  24.             int mid = l + r >> 1;
  25.             creatNode(u);
  26.             pushdown(u);
  27.             if (ql <= mid) modify(tr[u].idxl, l, mid, ql, qr, x);
  28.             if (qr > mid) modify(tr[u].idxr, mid + 1, r, ql, qr, x);
  29.             pushup(u);
  30.         }
  31.     }
  33.     int query(int u, int l, int r, int ql, int qr) {
  34.         if (ql <= l && qr >= r) {
  35.             return tr[u].height;
  36.         } else {
  37.             int mid = l + r >> 1;
  38.             creatNode(u);
  39.             pushdown(u);
  40.             int res = 0;
  41.             if (ql <= mid) res = Math.max(res, query(tr[u].idxl, l, mid, ql, qr));
  42.             if (qr > mid) res = Math.max(res, query(tr[u].idxr, mid + 1, r, ql, qr));
  43.             return res;
  44.         }
  45.     }
  47.     void pushup(int u) {
  48.         tr[u].height = Math.max(tr[tr[u].idxl].height, tr[tr[u].idxr].height);
  49.     }
  51.     void pushdown(int u) {
  52.         if (tr[u].add > 0) {
  53.             Node left = tr[tr[u].idxl], right = tr[tr[u].idxr];
  54.             left.height = tr[u].add;
  55.             left.add = tr[u].add;
  56.             right.height = tr[u].add;
  57.             right.add = tr[u].add;
  58.             tr[u].add = 0;
  59.         }
  60.     }
  62.     void creatNode(int u) {
  63.         if (tr[u] == null)
  64.             tr[u] = new Node();
  65.         if (tr[u].idxl == 0) {
  66.             tr[u].idxl = ++idx;
  67.             tr[idx] = new Node();
  68.         }
  69.         if (tr[u].idxr == 0) {
  70.             tr[u].idxr = ++idx;
  71.             tr[idx] = new Node();
  72.         }
  73.     }
  74. }

线段树.pdf

  • 挖个坑，非递归线段树

Efficient and easy segment trees
算法学习笔记(76): zkw线段树

参考

2019年8月XX日线段树讲义
https://codeforces.com/blog/entry/18051