可持久化的前提:
本身的拓扑结构不变
解决什么样的问题?
存储数据结构的所有历史版本,只记录每个版本与前一版本的不同(和更前版本无关)
一般都是二叉树!(线段树,01Trie, )
1. 可持久化线段树
又名:主席树
很难处理区间修改操作,除非将懒标记也持久化
AcWing 255. 第K小数
静态问题,解法有:
- 归并树
- 划分树
O(NlogN),空间复杂度:O(NlogN) - 主席树 时间复杂度:
O(NlogN), 空间复杂度:O(N(logN + 4))
如果是可修改的问题,解法有:
- 线段树套平衡树 时间复杂度:
O(Mlog2N),空间复杂度:O(MlogN) - 主席树套树状数组
本题思路: 可持久化线段树
离散化,[1, n-1]
在数值上建立线段树,维护每个数值区间中一共有多少个数
时间复杂度:O((N + M)logN)
空间复杂度:O(N(logN + 4)
问题1:求整体第k小数?
树上二分
问题2:有左右区间限制的第k小数
首先考虑[1, R],使用版本R即可
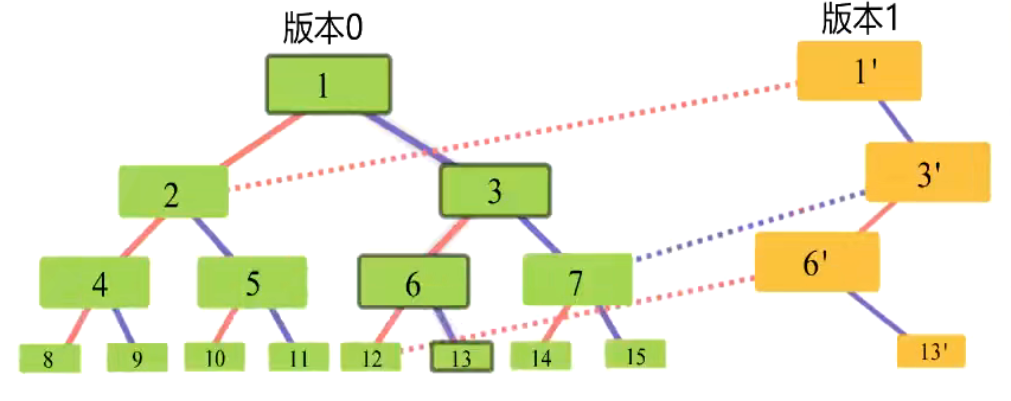
然后考虑[L, R],由于每个版本线段树的拓扑结构不变,同时在L-1和R版本上二分,类似于前缀和的思想
2. 可持久化Trie
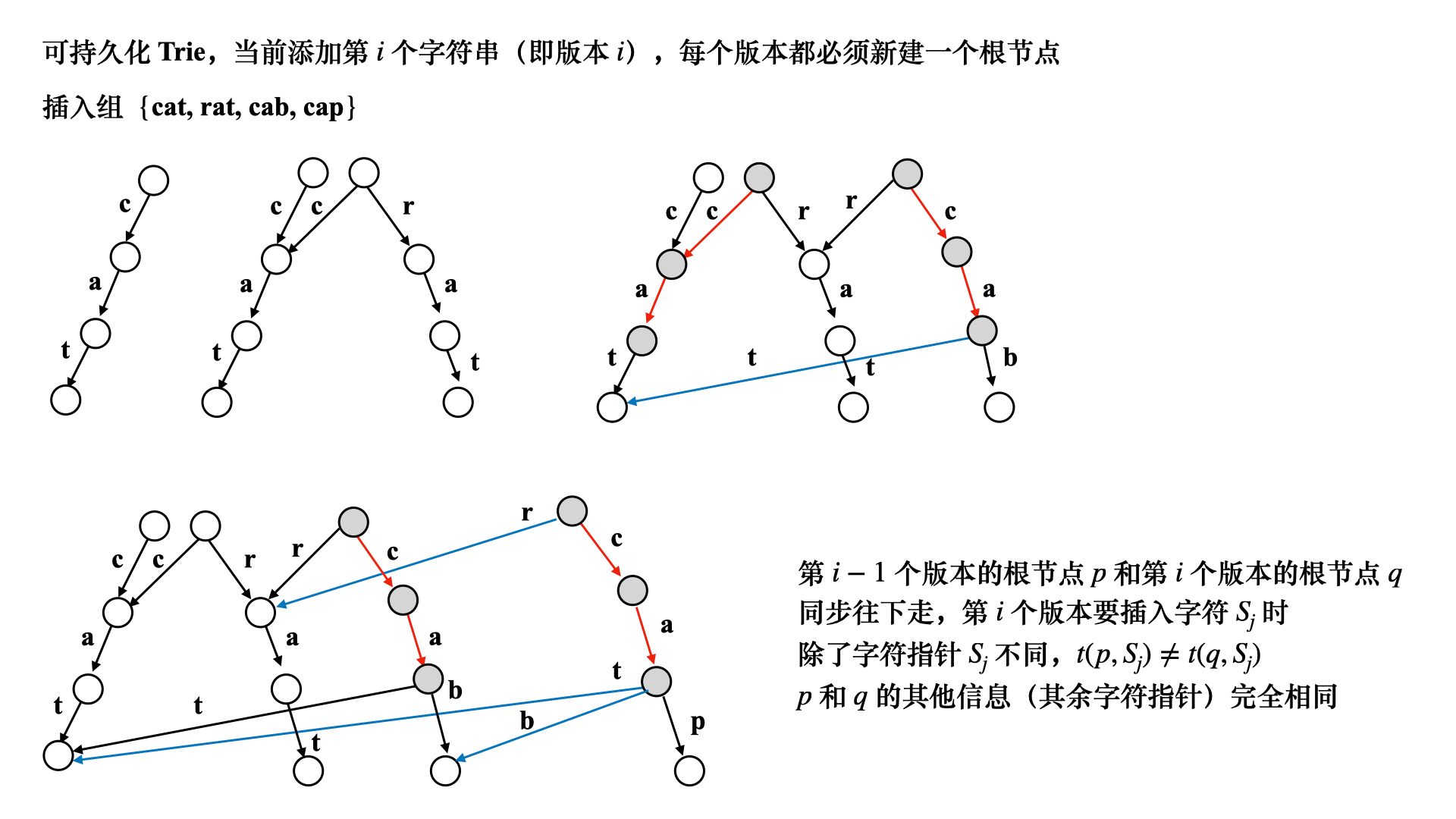
图来自 心里没有一点AC数
可持久化 Trie 的方式和可持久化线段树的方式是相似的,即每次只修改被添加或值被修改的节点,而保留没有被改动的节点,在上一个版本的基础上连边,使最后每个版本的 Trie 树的根遍历所能分离出的 Trie 树都是完整且包含全部信息的。
大部分的可持久化 Trie 题中,Trie 都是以 01-Trie 的形式出现的。
而01Trie本质上是权值线段树,只是划分方式有所区别
一般用来解决异或相关的能够按位贪心的题目。
AcWing 256. 最大异或和
思路:
维护所有版本的前缀异或和 ,维护可持久化trie
若当前版本为N,前缀异或和为SN
目标是从[l, r]中选一版本P使得Sp - 1 ^ SN ^ x最大
如果只是[1, r],问题很简单,只需要用版本r - 1的trie按位贪心即可
在加上左界l的限制后,只需要考虑每个权值的最后一次出现版本是否大于等于l - 1即可

