枚举元素个数为n的集和的所有子集

时间复杂度：O(2n)

  1. for (int i = 0; i < 1 << n; i++)
  2. {
  3.      // do something   
  4. }

枚举元素个数为n的集和的所有子集的所有子集

时间复杂度：O(3n)

  1. for (int st = 0; st < 1 << n; st++) {
  2.      for (int i = st; i > 0; i = st & (i - 1)) {
  3.          // do something   
  4.     }
  5. }

Acwing 487. 金明的预算方案

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间金明自己专用的很宽敞的房间。
更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过N元钱就行”。
今天一早，金明就开始做预算了，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子：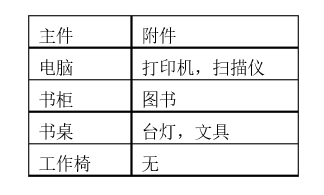
子集枚举 - 图1
如果要买归类为附件的物品，必须先买该附件所属的主件。
每个主件可以有0个、1个或2个附件。
附件不再有从属于自己的附件。
金明想买的东西很多，肯定会超过妈妈限定的N元。
于是，他把每件物品规定了一个重要度，分为5等：用整数1~5表示，第5等最重要。
他还从因特网上查到了每件物品的价格（都是10元的整数倍）。
他希望在不超过N元（可以等于N元）的前提下，使每件物品的价格与重要度的乘积的总和最大。
设第j件物品的价格为v[j]，重要度为w[j]，共选中了k件物品，编号依次为j1，j2，…，jk，则所求的总和为：
v[j1]∗w[j1]+v[j2]∗w[j2]+…+v[jk]∗w[jk]（其中*为乘号）
请你帮助金明设计一个满足要求的购物单。

输入格式
输入文件的第1行，为两个正整数，用一个空格隔开：N m，其中N表示总钱数，m为希望购买物品的个数。
从第2行到第m+1行，第j行给出了编号为j-1的物品的基本数据，每行有3个非负整数v p q，其中v表示该物品的价格，p表示该物品的重要度（1~5），q表示该物品是主件还是附件。
如果q=0，表示该物品为主件，如果q>0，表示该物品为附件，q是所属主件的编号。
输出格式
输出文件只有一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值（<200000）。
数据范围
N<32000,m<60,v<10000
输入样例：

  1. 1000 5
  2. 800 2 0
  3. 400 5 1
  4. 300 5 1
  5. 400 3 0
  6. 500 2 0

输出样例：
2200

思路:
稍稍改进的分组背包问题，每个附属物品购买的前提条件是主物品被购买
附属物品并不是全选或全不选，而是可以有选择的买，可以只买其中的某一样或者某两样等等

这时候就需要二进制来枚举每件附属物品是否备选，二进制的每一位代表一件物品，0表示没选，1表示选择
假设一组内有x件附属物品，需要枚举的情况有 [0, 1 << x), 也就是2``x种情况。

  1. import java.util.*;
  3. public class Main {
  4.     public static void main(String[] args) {
  5.         Scanner sc = new Scanner(System.in);
  7.         int m = sc.nextInt(), n = sc.nextInt();
  8.         Pair[] master = new Pair[n + 1];
  9.         List<Pair>[] list = new ArrayList[n + 1];
  11.         for (int i = 1; i <= n; i++) {
  12.             int v = sc.nextInt(), p = sc.nextInt(), q = sc.nextInt();
  13.             if (q == 0) {
  14.                 master[i] = new Pair(v, p * v);
  15.                 list[i] = new ArrayList<>();
  16.             } else {
  17.                 list[q].add(new Pair(v, p * v));
  18.             }
  19.         }
  21.         // for (int i = 0; i <= n; i++) {
  22.         //     if (list[i] != null)
  23.         //         System.out.println(i + " " + list[i].toString());
  24.         // }
  26.         int[] f = new int[m + 1];
  27.         for (int i = 1; i <= n; i++) {
  28.             if (master[i] != null) {
  29.                 for (int j = m; j >= 0; j--) {
  31.                     //二进制枚举
  32.                     for (int k = 0; k < 1 << list[i].size(); k++) {
  33.                         int v = master[i].v, w = master[i].w;
  34.                         //内层循环判断每件物品是否被选
  35.                         for (int u = 0; u < list[i].size(); u++) {
  36.                             if ((k >> u & 1) == 1) {
  37.                                 Pair p =  list[i].get(u);
  38.                                 v += p.v;
  39.                                 w += p.w;
  40.                             }
  41.                         }
  42.                         if (j >= v) f[j] = Math.max(f[j], f[j - v] + w);
  43.                     }
  44.                 }
  45.             }
  46.         }
  47.         System.out.println(f[m]);
  49.     }
  50. }
  52. class Pair {
  53.     int v, w;
  54.     Pair(int v, int w) {
  55.         this.v = v;
  56.         this.w = w;
  57.     }
  59.     public String toString() {
  60.         return this.v + " " + this.w;
  61.     }
  62. }

2002. 两个回文子序列长度的最大乘积

给你一个字符串 s ，请你找到 s 中两个 不相交回文子序列 ，使得它们长度的 乘积最大 。两个子序列在原字符串中如果没有任何相同下标的字符，则它们是 不相交 的。
请你返回两个回文子序列长度可以达到的 最大乘积 。
子序列 指的是从原字符串中删除若干个字符（可以一个也不删除）后，剩余字符不改变顺序而得到的结果。如果一个字符串从前往后读和从后往前读一模一样，那么这个字符串是一个 回文字符串 。

示例 1：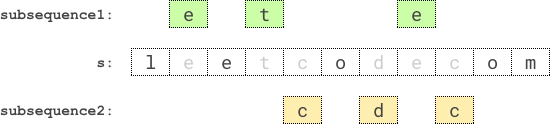
子集枚举 - 图2
输入：s = “leetcodecom”
输出：9
解释：最优方案是选择 “ete” 作为第一个子序列，”cdc” 作为第二个子序列。
它们的乘积为 3 * 3 = 9 。

示例 2：
输入：s = “bb”
输出：1
解释：最优方案为选择 “b” （第一个字符）作为第一个子序列，”b” （第二个字符）作为第二个子序列。
它们的乘积为 1 * 1 = 1 。

示例 3：
输入：s = “accbcaxxcxx”
输出：25
解释：最优方案为选择 “accca” 作为第一个子序列，”xxcxx” 作为第二个子序列。
它们的乘积为 5 * 5 = 25 。

提示：

  • 2 <= s.length <= 12
  • s 只含有小写英文字母。
  1. class Solution {
  2.     public int maxProduct(String s) {
  3.         int n = s.length();
  4.         List<Integer> bit = new ArrayList<>();
  5.         List<Integer> len = new ArrayList<>();
  7.         for (int i = 0; i < 1 << n; i++) {
  8.             StringBuilder sb = new StringBuilder();
  9.             int x = 0;
  10.             for (int j = 0; j < n; j++) {
  11.                 if ((i >> j & 1) == 1) {
  12.                     sb.append(s.charAt(j));
  13.                     x++;
  14.                 }
  15.             }
  16.             if (check(sb.toString())) {
  17.                 bit.add(i);
  18.                 len.add(x);
  19.             }
  20.         }
  22.         int ans = 0;
  23.         for (int i = 0; i < bit.size(); i++) {
  24.             for (int j = i + 1; j < bit.size(); j++) {
  25.                 int a = bit.get(i), b = bit.get(j);
  26.                 if ((a & b) == 0)
  27.                     ans = Math.max(ans, len.get(i) * len.get(j));
  28.             }
  29.         }
  30.         return ans;
  31.     }
  33.     boolean check(String s) {
  34.         int l = 0, r = s.length() - 1;
  35.         while (l < r) {
  36.             if (s.charAt(l) != s.charAt(r))
  37.                 return false;
  38.             l++;
  39.             r--;
  40.         }
  41.         return true;
  42.     }
  43. }