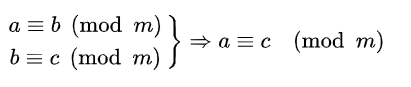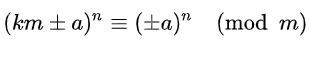数学上，同余（英语：congruence modulo，符号：≡）是数论中的一种等价关系

当两个整数除以同一个正整数，若得相同余数，则二整数同余。
两个整数a，b，若它们除以正整数m所得的余数相等，则称a，b对于模m同余。
记作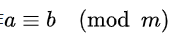
image.png
读作a同余b模m或者a与b对模m同余

同余符号

≡，Unicode码值为 \u2261

性质

整除性

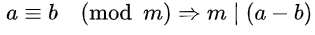
image.png
a，b对于模m同余等价于m能整除a-b

传递性

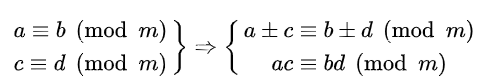
image.png

保持基本运算

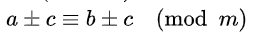
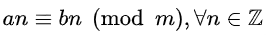
image.png
若c = d，可得：
image.png
image.png

若c = a，b = d，可得：
image.png

放大缩小底数

k为整数，n为正整数，有
image.png
证明：使用二项式定理即可

放大缩小模数

k为正整数，
a ``≡ b(mod m) 当且仅当 ka ``≡ kb(mod km)

除法原理1

若ka ≡ kb(mod m)且k与m互质，则a ``≡ b(mod m)

除法定理2

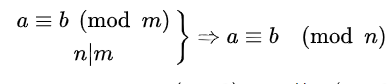
image.png

n|m表示n能整除m，或者m能被n整除，意思是m%n=0

同余式

ax = b ( mod c ) <==> ax + cy = b
有解的充要条件是(a, c) | b