🏆 第 305 场力扣周赛

最后一题着急了，越急越容易出错！

6136. 算术三元组的数目

给你一个下标从 0 开始、严格递增 的整数数组 nums 和一个正整数 diff 。如果满足下述全部条件，则三元组 (i, j, k) 就是一个 算术三元组 ：

• i < j < k ，
• nums[j] - nums[i] == diff 且
• nums[k] - nums[j] == diff

返回不同 算术三元组 的数目。

示例 1：
输入：nums = [0,1,4,6,7,10], diff = 3 输出：2 解释： (1, 2, 4) 是算术三元组：7 - 4 == 3 且 4 - 1 == 3 。 (2, 4, 5) 是算术三元组：10 - 7 == 3 且 7 - 4 == 3 。
示例 2：
输入：nums = [4,5,6,7,8,9], diff = 2 输出：2 解释： (0, 2, 4) 是算术三元组：8 - 6 == 2 且 6 - 4 == 2 。 (1, 3, 5) 是算术三元组：9 - 7 == 2 且 7 - 5 == 2 。

提示：

• 3 <= nums.length <= 200
• 0 <= nums[i] <= 200
• 1 <= diff <= 50
• nums 严格 递增

思路：
暴力

class Solution {
    public int arithmeticTriplets(int[] nums, int d) {
        int n = nums.length;
        int c = 0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                for (int k = j + 1; k < n; k++) {
                    if (nums[k] - nums[j] == d && nums[j] - nums[i] == d)
                        c++;
                }
            }
        }
        return c;
    }   
}

6139. 受限条件下可到达节点的数目

现有一棵由 n 个节点组成的无向树，节点编号从 0 到 n - 1 ，共有 n - 1 条边。
给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。
在不访问受限节点的前提下，返回你可以从节点 _0 到达的 最多 节点数目。_
注意，节点 0 不 会标记为受限节点。

示例 1：
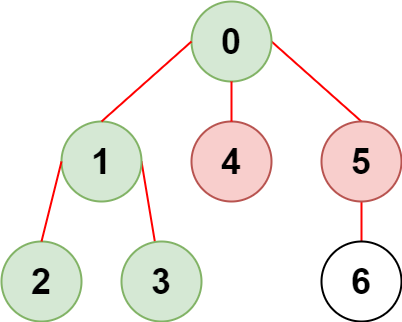
输入：n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5] 输出：4 解释：上图所示正是这棵树。 在不访问受限节点的前提下，只有节点 [0,1,2,3] 可以从节点 0 到达。
示例 2：
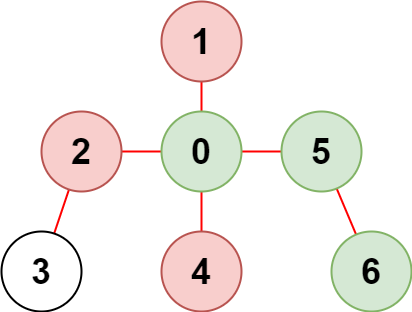
输入：n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1] 输出：3 解释：上图所示正是这棵树。 在不访问受限节点的前提下，只有节点 [0,5,6] 可以从节点 0 到达。

提示：

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges 表示一棵有效的树
• 1 <= restricted.length < n
• 1 <= restricted[i] < n
• restricted 中的所有值 互不相同

思路：
并查集找与0连通的节点数

class Solution {
    int N = 100010;
    int[] fa = new int[N];
    int[] s = new int[N];
    public int reachableNodes(int n, int[][] e, int[] r) {
        for (int i = 0; i < n; i++) {
            fa[i] = i;
            s[i] = 1;
        }
        Set<Integer> set = new HashSet<>();
        for (int x : r) set.add(x);
        for (int[] p : e) {
            int a = p[0], b = p[1];
            if (set.contains(a) || set.contains(b))
                continue;
            merge(a, b);
        }
        return s[find(0)];
    }
    void merge(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa != pb) {
            fa[pa] = pb;
            s[pb] += s[pa];
        }
    }
    int find(int x) {
        return x == fa[x] ? x : (fa[x] = find(fa[x]));
    }
}

6137. 检查数组是否存在有效划分

给你一个下标从 0 开始的整数数组 nums ，你必须将数组划分为一个或多个 连续 子数组。
如果获得的这些子数组中每个都能满足下述条件 之一 ，则可以称其为数组的一种 有效 划分：

1. 子数组 恰 由 2 个相等元素组成，例如，子数组 [2,2] 。
2. 子数组 恰 由 3 个相等元素组成，例如，子数组 [4,4,4] 。
3. 子数组 恰 由 3 个连续递增元素组成，并且相邻元素之间的差值为 1 。例如，子数组 [3,4,5] ，但是子数组 [1,3,5] 不符合要求。

如果数组 至少 存在一种有效划分，返回 true ，否则，返回 false 。

示例 1：
输入：nums = [4,4,4,5,6] 输出：true 解释：数组可以划分成子数组 [4,4] 和 [4,5,6] 。 这是一种有效划分，所以返回 true 。
示例 2：
输入：nums = [1,1,1,2] 输出：false 解释：该数组不存在有效划分。

提示：

• 2 <= nums.length <= 105
• 1 <= nums[i] <= 106

思路：
DP

class Solution {
    public boolean validPartition(int[] nums) {
        int n = nums.length;
        boolean[] st = new boolean[n];
        for (int i = 1; i < n; i++) {
            if (i - 1 >= 0 && nums[i] == nums[i - 1]) {
                if (i - 2 >= 0) st[i] = st[i] || st[i - 2];
                else st[i] = true;
            }
            if (i - 2 >= 0 && nums[i] == nums[i - 1] && nums[i - 1] == nums[i - 2]) {
                if (i - 3 >= 0) st[i] = st[i] || st[i - 3];
                else st[i] = true;
            }
            if (i - 2 >= 0 && nums[i] - 1 == nums[i - 1] && nums[i - 1] - 1 == nums[i - 2]) {
                if (i - 3 >= 0) st[i] = st[i] || st[i - 3];
                else st[i] = true;
            }
        }
        return st[n - 1];
    }
}

6138. 最长理想子序列

给你一个由小写字母组成的字符串 s ，和一个整数 k 。如果满足下述条件，则可以将字符串 t 视作是 理想字符串 ：

• t 是字符串 s 的一个子序列。
• t 中每两个 相邻 字母在字母表中位次的绝对差值小于或等于 k 。

返回 最长 理想字符串的长度。
字符串的子序列同样是一个字符串，并且子序列还满足：可以经由其他字符串删除某些字符（也可以不删除）但不改变剩余字符的顺序得到。
注意：字母表顺序不会循环。例如，’a’ 和 ‘z’ 在字母表中位次的绝对差值是 25 ，而不是 1 。

示例 1：
输入：s = “acfgbd”, k = 2 输出：4 解释：最长理想字符串是 “acbd” 。该字符串长度为 4 ，所以返回 4 。 注意 “acfgbd” 不是理想字符串，因为 ‘c’ 和 ‘f’ 的字母表位次差值为 3 。
示例 2：
输入：s = “abcd”, k = 3 输出：4 解释：最长理想字符串是 “abcd” ，该字符串长度为 4 ，所以返回 4 。

提示：

• 1 <= s.length <= 105
• 0 <= k <= 25
• s 由小写英文字母组成

思路：
DP
时间复杂度：O(|Sigmund|N)

class Solution {
    public int longestIdealString(String s, int k) {
        int[] f = new int[26];
        for (int i = 0; i < s.length(); i++) {
            int x = s.charAt(i) - 'a';
            int v = 1;
            for (int j = 0; j < 26; j++) {
                if (Math.abs(j - x) <= k)
                    v = Math.max(v, f[j] + 1);
            }
            f[x] = v;
        }
        int max = 0;
        for (int x : f) max = Math.max(max, x);
        return max;
    }
}