6027. 统计数组中峰和谷的数量

给你一个下标从 0 开始的整数数组 nums 。如果两侧距 i 最近的不相等邻居的值均小于 nums[i] ，则下标 i 是 nums 中，某个峰的一部分。类似地，如果两侧距 i 最近的不相等邻居的值均大于 nums[i] ，则下标 i 是 nums 中某个谷的一部分。对于相邻下标 i 和 j ，如果 nums[i] == nums[j] ， 则认为这两下标属于 同一个 峰或谷。
注意，要使某个下标所做峰或谷的一部分，那么它左右两侧必须 都 存在不相等邻居。
返回 nums 中峰和谷的数量。

示例 1：
输入：nums = [2,4,1,1,6,5] 输出：3 解释： 在下标 0 ：由于 2 的左侧不存在不相等邻居，所以下标 0 既不是峰也不是谷。 在下标 1 ：4 的最近不相等邻居是 2 和 1 。由于 4 > 2 且 4 > 1 ，下标 1 是一个峰。 在下标 2 ：1 的最近不相等邻居是 4 和 6 。由于 1 < 4 且 1 < 6 ，下标 2 是一个谷。 在下标 3 ：1 的最近不相等邻居是 4 和 6 。由于 1 < 4 且 1 < 6 ，下标 3 符合谷的定义，但需要注意它和下标 2 是同一个谷的一部分。 在下标 4 ：6 的最近不相等邻居是 1 和 5 。由于 6 > 1 且 6 > 5 ，下标 4 是一个峰。 在下标 5 ：由于 5 的右侧不存在不相等邻居，所以下标 5 既不是峰也不是谷。 共有 3 个峰和谷，所以返回 3 。
示例 2：
输入：nums = [6,6,5,5,4,1] 输出：0 解释： 在下标 0 ：由于 6 的左侧不存在不相等邻居，所以下标 0 既不是峰也不是谷。 在下标 1 ：由于 6 的左侧不存在不相等邻居，所以下标 1 既不是峰也不是谷。 在下标 2 ：5 的最近不相等邻居是 6 和 4 。由于 5 < 6 且 5 > 4 ，下标 2 既不是峰也不是谷。 在下标 3 ：5 的最近不相等邻居是 6 和 4 。由于 5 < 6 且 5 > 4 ，下标 3 既不是峰也不是谷。 在下标 4 ：4 的最近不相等邻居是 5 和 1 。由于 4 < 5 且 4 > 1 ，下标 4 既不是峰也不是谷。 在下标 5 ：由于 1 的右侧不存在不相等邻居，所以下标 5 既不是峰也不是谷。 共有 0 个峰和谷，所以返回 0 。

提示：

  • 3 <= nums.length <= 100
  • 1 <= nums[i] <= 100

思路：
模拟题

  1. class Solution {
  2.     public int countHillValley(int[] nums) {
  3.         int cnt = 0;
  4.         for (int i = 0; i < nums.length; i ++) {
  5.             int l = i - 1, r  = i + 1;
  6.             while (l >= 0 && nums[l] == nums[i])
  7.                 l--;
  9.             while (r < nums.length && nums[r] == nums[i])
  10.                 r++;
  11.             if (l >= 0 && r < nums.length && ((nums[l] > nums[i] && nums[r] > nums[i]) || (nums[l] < nums[i] && nums[r] < nums[i])))
  12.                 cnt++;
  13.             i = r - 1;
  14.         }
  15.         return cnt;
  16.     }
  17. }

6028. 统计道路上的碰撞次数

在一条无限长的公路上有 n 辆汽车正在行驶。汽车按从左到右的顺序按从 0 到 n - 1 编号，每辆车都在一个 独特的 位置。
给你一个下标从 0 开始的字符串 directions ，长度为 n 。directions[i] 可以是 ‘L’、’R’ 或 ‘S’ 分别表示第 i 辆车是向 左 、向 右 或者 停留 在当前位置。每辆车移动时 速度相同 。
碰撞次数可以按下述方式计算：

  • 当两辆移动方向 相反 的车相撞时，碰撞次数加 2 。
  • 当一辆移动的车和一辆静止的车相撞时，碰撞次数加 1 。

碰撞发生后，涉及的车辆将无法继续移动并停留在碰撞位置。除此之外，汽车不能改变它们的状态或移动方向。
返回在这条道路上发生的 碰撞总次数 。

示例 1：
输入：directions = “RLRSLL” 输出：5 解释： 将会在道路上发生的碰撞列出如下： - 车 0 和车 1 会互相碰撞。由于它们按相反方向移动，碰撞数量变为 0 + 2 = 2 。 - 车 2 和车 3 会互相碰撞。由于 3 是静止的，碰撞数量变为 2 + 1 = 3 。 - 车 3 和车 4 会互相碰撞。由于 3 是静止的，碰撞数量变为 3 + 1 = 4 。 - 车 4 和车 5 会互相碰撞。在车 4 和车 3 碰撞之后，车 4 会待在碰撞位置，接着和车 5 碰撞。碰撞数量变为 4 + 1 = 5 。 因此，将会在道路上发生的碰撞总次数是 5 。
示例 2：
输入：directions = “LLRR” 输出：0 解释： 不存在会发生碰撞的车辆。因此，将会在道路上发生的碰撞总次数是 0 。

提示：

  • 1 <= directions.length <= 105
  • directions[i] 的值为 ‘L’、’R’ 或 ‘S’

思路：
除了最长向左前缀和最长向右后缀外，其余车辆均会碰撞，去除那些一开始就是S状态的就是碰撞次数
比赛的时候写的有点麻烦，硬模拟了

  1. class Solution {
  2.     public int countCollisions(String s) {
  3.         int n = s.length();
  4.         int i = 0, j = n - 1;
  5.         while (i < n && s.charAt(i) == 'L')
  6.                 i++;
  7.         while (j >= 0 && s.charAt(j) == 'R')
  8.                 j--;
  9.         int cnt = 0;
  10.         for (int k = i; k <= j; k++)
  11.             if (s.charAt(k) != 'S')
  12.                 cnt++;
  13.         return cnt;
  14.     }
  15. }

6029. 射箭比赛中的最大得分

Alice 和 Bob 是一场射箭比赛中的对手。比赛规则如下：

  1. Alice 先射 numArrows 支箭，然后 Bob 也射 numArrows 支箭。
  2. 分数按下述规则计算：
    1. 箭靶有若干整数计分区域，范围从 0 到 11 （含 0 和 11）。
    2. 箭靶上每个区域都对应一个得分 k（范围是 0 到 11），Alice 和 Bob 分别在得分 k 区域射中 ak 和 bk 支箭。如果 ak >= bk ，那么 Alice 得 k 分。如果 ak < bk ，则 Bob 得 k 分
    3. 如果 ak == bk == 0 ，那么无人得到 k 分。
  • 例如，Alice 和 Bob 都向计分为 11 的区域射 2 支箭，那么 Alice 得 11 分。如果 Alice 向计分为 11 的区域射 0 支箭，但 Bob 向同一个区域射 2 支箭，那么 Bob 得 11 分。

给你整数 numArrows 和一个长度为 12 的整数数组 aliceArrows ，该数组表示 Alice 射中 0 到 11 每个计分区域的箭数量。现在，Bob 想要尽可能 最大化 他所能获得的总分。
返回数组 bobArrows ，该数组表示 Bob 射中 0 到 11 每个 计分区域的箭数量。且 bobArrows 的总和应当等于 numArrows 。
如果存在多种方法都可以使 Bob 获得最大总分，返回其中 任意一种 即可。

示例 1：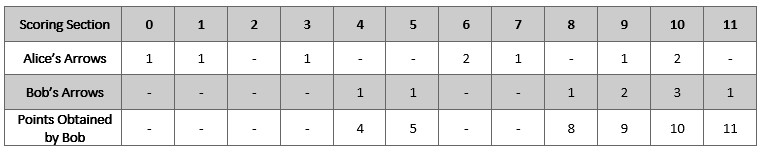
image.png
输入：numArrows = 9, aliceArrows = [1,1,0,1,0,0,2,1,0,1,2,0] 输出：[0,0,0,0,1,1,0,0,1,2,3,1] 解释：上表显示了比赛得分情况。 Bob 获得总分 4 + 5 + 8 + 9 + 10 + 11 = 47 。 可以证明 Bob 无法获得比 47 更高的分数。
示例 2：
image.png
输入：numArrows = 3, aliceArrows = [0,0,1,0,0,0,0,0,0,0,0,2] 输出：[0,0,0,0,0,0,0,0,1,1,1,0] 解释：上表显示了比赛得分情况。 Bob 获得总分 8 + 9 + 10 = 27 。 可以证明 Bob 无法获得比 27 更高的分数。

提示：

  • 1 <= numArrows <= 105
  • aliceArrows.length == bobArrows.length == 12
  • 0 <= aliceArrows[i], bobArrows[i] <= numArrows
  • sum(aliceArrows[i]) == numArrows

思路：
二进制枚举 找最优解

  1. class Solution {
  2.     public int[] maximumBobPoints(int x, int[] a) {
  4.         int n = 12;
  5.         int[] res = new int[n];
  7.         int max = 0, v = 0;
  8.         for (int i = 0; i < 1 << n; i++) {
  9.             int sum = 0;
  10.             int cnt = 0;
  11.             for (int j = 0; j < n; j++) {
  12.                 if ((i >> j & 1) == 1) {
  13.                     cnt += a[j] + 1;
  14.                     sum += j;
  15.                 }
  16.             }
  17.             if (cnt <= x && sum > max) {
  18.                 max = sum;
  19.                 v = i;
  20.             }
  21.         }
  23.         int cnt = 0;
  24.         int sum = 0;
  25.         for (int i = 0; i < n; i++) {
  26.             if ((v >> i & 1) == 1) {
  27.                 res[i] = a[i] + 1;
  28.                 cnt += res[i];
  29.                 sum += i;
  30.             }
  31.         } 
  32.         // System.out.println(sum);
  33.         if (x > cnt) res[0] += x - cnt;
  34.         return res;
  35.     }
  36. }

6030. 由单个字符重复的最长子字符串

给你一个下标从 0 开始的字符串 s 。另给你一个下标从 0 开始、长度为 k 的字符串 queryCharacters ，一个下标从 0 开始、长度也是 k 的整数 下标 数组 queryIndices ，这两个都用来描述 k 个查询。
第 i 个查询会将 s 中位于下标 queryIndices[i] 的字符更新为 queryCharacters[i] 。
返回一个长度为 k 的数组 lengths ，其中 lengths[i] 是在执行第 i 个查询 之后 s 中仅由 单个字符重复 组成的 最长子字符串 的 长度 。

示例 1：
输入：s = “babacc”, queryCharacters = “bcb”, queryIndices = [1,3,3] 输出：[3,3,4] 解释： - 第 1 次查询更新后 s = “bbb_acc” 。由单个字符重复组成的最长子字符串是 “bbb” ，长度为 3 。 - 第 2 次查询更新后 s = “bbbccc“ 。由单个字符重复组成的最长子字符串是 “bbb” 或 “ccc”，长度为 3 。 - 第 3 次查询更新后 s = “_bbbb_cc” 。由单个字符重复组成的最长子字符串是 “bbbb” ，长度为 4 。 因此，返回 [3,3,4] 。
示例 2：
输入：s = “abyzz”, queryCharacters = “aa”, queryIndices = [2,1] 输出：[2,3] 解释： - 第 1 次查询更新后 s = “aba_zz“ 。由单个字符重复组成的最长子字符串是 “zz” ，长度为 2 。 - 第 2 次查询更新后 s = “_aaa_zz” 。由单个字符重复组成的最长子字符串是 “aaa” ，长度为 3 。 因此，返回 [2,3] 。

提示：

  • 1 <= s.length <= 105
  • s 由小写英文字母组成
  • k == queryCharacters.length == queryIndices.length
  • 1 <= k <= 105
  • queryCharacters 由小写英文字母组成
  • 0 <= queryIndices[i] < s.length

思路：
线段树板子题
单点修改，区间查询

  1. class Solution {
  2.     final int N = 100010;
  3.     int n, m;
  4.     Node[] tr = new Node[4 * N];
  5.     char[] ch;
  6.     public int[] longestRepeating(String s, String qc, int[] qidx) {
  7.         ch = s.toCharArray();
  8.         n = ch.length;
  9.         m = qidx.length;
  10.         build(1, 0, n - 1);
  11.         int[] res = new int[m];
  12.         for (int i = 0; i < m; i++) {
  13.             modify(1, qidx[i], qc.charAt(i));
  14.             res[i] = tr[1].max;
  15.         }
  16.         return res;
  17.     }
  19.     void build(int u, int l, int r) {
  20.         if (l == r) {
  21.             tr[u] = new Node(l, r);
  22.             tr[u].lmax = tr[u].rmax = tr[u].max = tr[u].len = 1;
  23.         } else {
  24.             tr[u] = new Node(l, r);
  25.             int mid = l + r >> 1;
  26.             build(u << 1, l, mid);
  27.             build(u << 1 | 1, mid + 1, r);
  28.             pushup(u);
  29.         }
  30.     }
  32.     void pushup(int u) {
  33.         Node left = tr[u << 1], right = tr[u << 1 | 1];
  34.         tr[u].len = left.len + right.len;
  35.         tr[u].max = Math.max(left.max, right.max);
  36.         tr[u].lmax = left.lmax;
  37.         tr[u].rmax = right.rmax;
  38.         int mid = tr[u].l + tr[u].r >> 1;
  39.         if (ch[mid] == ch[mid + 1]) {
  40.             tr[u].max = Math.max(tr[u].max, left.rmax + right.lmax);
  41.             if (left.len == left.lmax)
  42.                 tr[u].lmax = Math.max(tr[u].lmax, left.len + right.lmax);
  43.             if (right.len == right.rmax)
  44.                 tr[u].rmax = Math.max(tr[u].rmax, right.len + left.rmax);
  45.         }
  46.     }
  48.     void modify(int u, int idx, char c) {
  49.         if (tr[u].l == idx && tr[u].r == idx) {
  50.             ch[idx] = c;
  51.             return;
  52.         } else {
  53.             int mid = tr[u].l + tr[u].r >> 1;
  54.             if (idx <= mid) modify(u << 1, idx, c);
  55.             else modify(u << 1 | 1, idx, c);
  56.             pushup(u);
  57.         }
  58.     }
  59. }
  61. class Node {
  62.     int l, r;
  63.     int max, len;
  64.     int lmax, rmax;
  65.     Node(int l,  int r) {
  66.         this.l = l;
  67.         this.r = r;
  68.     }
  69. }