😺 第 73 场力扣夜喵双周赛

6024. 数组中紧跟 key 之后出现最频繁的数字

思路：
模拟即可

5217. 将杂乱无章的数字排序

思路：
按照给定要求排序，注意溢出问题即可

2192. 有向无环图中一个节点的所有祖先

给你一个正整数 n ，它表示一个 有向无环图 中节点的数目，节点编号为 0 到 n - 1 （包括两者）。
给你一个二维整数数组 edges ，其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。
请你返回一个数组 answer，其中_ _answer[i]是第 i 个节点的所有 祖先 ，这些祖先节点 升序 排序。
如果 u 通过一系列边，能够到达 v ，那么我们称节点 u 是节点 v 的 祖先 节点。

示例 1：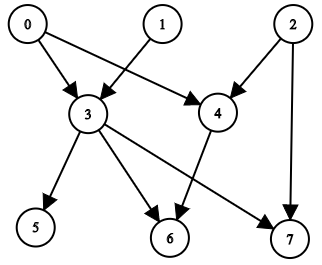

输入：n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]] 输出：[[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]] 解释： 上图为输入所对应的图。 - 节点 0 ，1 和 2 没有任何祖先。 - 节点 3 有 2 个祖先 0 和 1 。 - 节点 4 有 2 个祖先 0 和 2 。 - 节点 5 有 3 个祖先 0 ，1 和 3 。 - 节点 6 有 5 个祖先 0 ，1 ，2 ，3 和 4 。 - 节点 7 有 4 个祖先 0 ，1 ，2 和 3 。
示例 2：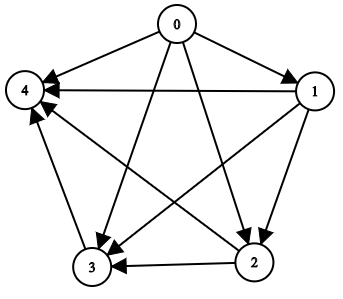

输入：n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]] 输出：[[],[0],[0,1],[0,1,2],[0,1,2,3]] 解释： 上图为输入所对应的图。 - 节点 0 没有任何祖先。 - 节点 1 有 1 个祖先 0 。 - 节点 2 有 2 个祖先 0 和 1 。 - 节点 3 有 3 个祖先 0 ，1 和 2 。 - 节点 4 有 4 个祖先 0 ，1 ，2 和 3 。

提示：

• 1 <= n <= 1000
• 0 <= edges.length <= min(2000, n * (n - 1) / 2)
• edges[i].length == 2
• 0 <= fromi, toi <= n - 1
• fromi != toi
• 图中不会有重边。
• 图是 有向 且 无环 的。

思路：
拓扑排序 + 有序集和

class Solution {
    int n;
    int[] h = new int[1010], e = new int[2010], ne = new int[2010];
    int idx;
    TreeSet<Integer>[] res = new TreeSet[1010];
    int[] in = new int[1010];
    public List<List<Integer>> getAncestors(int n, int[][] edges) {
        this.n = n;
        for (int i = 0; i < n; i++)
                res[i] = new TreeSet<>();
        Arrays.fill(h, -1);
        for (int[] p : edges) {
            int a = p[0], b = p[1];
            add(a, b);
            in[b]++;
        }
        Queue<Integer> q = new LinkedList<>();
        for (int i = 0; i < n; i++)
            if (in[i] == 0)
                q.offer(i);
        while (!q.isEmpty()) {
            int cur = q.poll();
            TreeSet<Integer> list = res[cur];
            for (int i = h[cur]; i != -1; i = ne[i]) {
                int j = e[i];
                TreeSet<Integer> l2 = res[j];
                for (int x : list)
                    l2.add(x);
                l2.add(cur);
                in[j]--;
                if (in[j] == 0)
                    q.offer(j);
            }
        }
        List<List<Integer>> ans = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            List<Integer> l = new ArrayList<>();
            for (int x : res[i])
                    l.add(x);
            ans.add(l);
        }
        return ans;
    }
    void add(int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}

2193. 得到回文串的最少操作次数

给你一个只包含小写英文字母的字符串 s 。
每一次 操作 ，你可以选择 s 中两个 相邻 的字符，并将它们交换。
请你返回将 s 变成回文串的 最少操作次数 。
注意 ，输入数据会确保 s 一定能变成一个回文串。

示例 1：
输入：s = “aabb” 输出：2 解释： 我们可以将 s 变成 2 个回文串，”abba” 和 “baab” 。 - 我们可以通过 2 次操作得到 “abba” ：”aab_b” -> “abab“ -> “abba” 。 - 我们可以通过 2 次操作得到 “baab” ：”aabb” -> “abab” -> “baab” 。 因此，得到回文串的最少总操作次数为 2 。
示例 2：
输入：s = “letelt” 输出：2 解释： 通过 2 次操作从 s 能得到回文串 “lettel” 。 其中一种方法是：”letelt“ -> “letet_l” -> “lettel” 。 其他回文串比方说 “tleelt” 也可以通过 2 次操作得到。 可以证明少于 2 次操作，无法得到回文串。

提示：

• 1 <= s.length <= 2000
• s 只包含小写英文字母。
• s 可以通过有限次操作得到一个回文串。

思路：
贪心题，证明待写
奇数串特殊处理下中间字符
考虑顺序处理前一半字符，通过移动使得其对应位置有和它相同的字符，并统计移动次数

class Solution {
    public int minMovesToMakePalindrome(String s) {
        int cnt = 0;
        char[] c = s.toCharArray();
        int n = c.length;
        int j = n - 1;
        for (int i = 0; i < j; i++) {
            for (int k = j; k >= i; k--) {
                if (i == k) {
                    cnt += n / 2 - i;
                } else if (c[i] == c[k]) {
                    for (int l = k; l < j; l++) {
                        c[l] = c[l + 1];
                        cnt++;
                    }
                    j--;
                    break;
                }
            }
        }        
        return cnt;
    }
}