问题描述

数数枪毙问题，共n个人，编号从0到n-1，从编号为0的人开始数1，编号为k - 1的人数k，数到k的人被枪毙。
从k开始再次从1数起，直至最后仅存一人。
1823. 找出游戏的获胜者
共有 n 名小伙伴一起做游戏。小伙伴们围成一圈，按 顺时针顺序 从 1 到 n 编号。确切地说，从第 i 名小伙伴顺时针移动一位会到达第 (i+1) 名小伙伴的位置，其中 1 <= i < n ，从第 n 名小伙伴顺时针移动一位会回到第 1 名小伙伴的位置。

游戏遵循如下规则：
从第 1 名小伙伴所在位置 开始 。
沿着顺时针方向数 k 名小伙伴，计数时需要 包含 起始时的那位小伙伴。逐个绕圈进行计数，一些小伙伴可能会被数过不止一次。
你数到的最后一名小伙伴需要离开圈子，并视作输掉游戏。
如果圈子中仍然有不止一名小伙伴，从刚刚输掉的小伙伴的 顺时针下一位 小伙伴 开始，回到步骤 2 继续执行。
否则，圈子中最后一名小伙伴赢得游戏。
给你参与游戏的小伙伴总数 n ，和一个整数 k ，返回游戏的获胜者。

示例 1：
输入：n = 5, k = 2
输出：3
解释：游戏运行步骤如下：
1) 从小伙伴 1 开始。
2) 顺时针数 2 名小伙伴，也就是小伙伴 1 和 2 。
3) 小伙伴 2 离开圈子。下一次从小伙伴 3 开始。
4) 顺时针数 2 名小伙伴，也就是小伙伴 3 和 4 。
5) 小伙伴 4 离开圈子。下一次从小伙伴 5 开始。
6) 顺时针数 2 名小伙伴，也就是小伙伴 5 和 1 。
7) 小伙伴 1 离开圈子。下一次从小伙伴 3 开始。
8) 顺时针数 2 名小伙伴，也就是小伙伴 3 和 5 。
9) 小伙伴 5 离开圈子。只剩下小伙伴 3 。所以小伙伴 3 是游戏的获胜者。

示例 2：
输入：n = 6, k = 5
输出：1
解释：小伙伴离开圈子的顺序：5、4、6、2、3 。小伙伴 1 是游戏的获胜者。

提示：
1 <= k <= n <= 500

思路

坐标系转换问题
f(n, k) 表示有n个人，从1数到k，枪毙第k个人，最后活着的人在[0, n - 1]中的节点编号
f(n - 1, k) n - 1个人，从1数到k，枪毙第k个人，最后活着的人在[0, n - 2]中的节点编号
假设最后活着的人在当前队伍中编号为x，映射回上一层序列为 (x + k) % n
这个式子是怎么来的？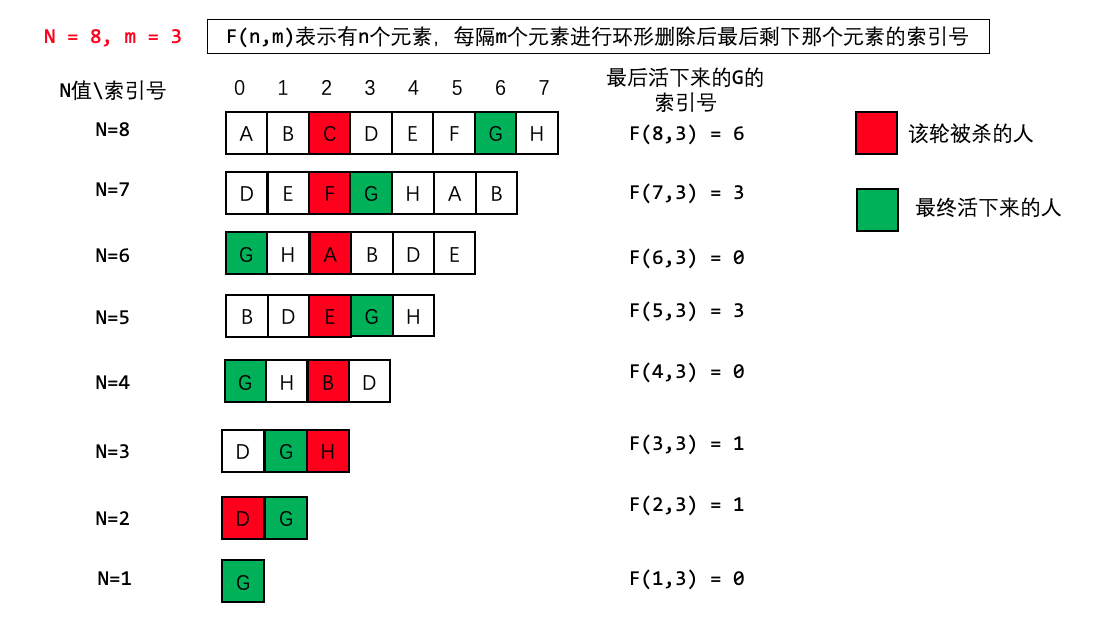
约瑟夫环 - 图1
每一轮都会死一个人，那么幸存者的位置每次都会前移m位，而且是循环前移
倒退无非是其逆过程，故 f(n, m) = f((n - 1, m) + m )% n
或者说上一轮删除了第 m 个位置，索引从 0 开始。因此本轮的索引 0 就是上一轮的索引 m。幸存者在本轮的索引为 f(n - 1, m) 则其在上一轮的索引为 f(n - 1, m) + m 由于上一轮共n个人，所以得处理下越界的问题！
综上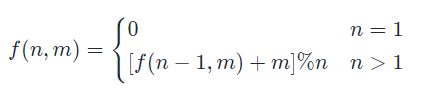： image.png
可以用递归或者迭代来写
从最后仅存一个人时的坐标倒推回其在所有人都存在时的坐标系下的坐标

  1. //递归
  2. class Solution {
  3.     public int findTheWinner(int n, int k) {
  4.         return f(n, k) + 1;
  5.     }
  7.     int f(int n, int k) {
  8.         if (n == 1)
  9.             return 0;
  11.         return (f(n - 1, k) + k) % n;
  12.     }
  13. }
  15. //迭代
  16. class Solution {
  17.     public int findTheWinner(int n, int k) {
  18.         int ans = 0;
  20.         for (int i = 2; i <= n; i++) {
  21.             ans = (ans + k) % i;
  22.         }
  23.         return ans + 1;
  24.     }
  25. }

进阶问题

1455. 招聘
不同的是，k不再是固定的，而是一个数组，依次循环使用数组中的元素作为k。
f(x) = (f(x - 1) + a[(n - x) % m]) % x

  1. import java.util.*;
  3. public class Main {
  4.     public static void main(String[] args) {
  5.         Scanner sc = new Scanner(System.in);
  7.         int t = sc.nextInt();
  8.         while (t-- > 0) {
  9.             int n = sc.nextInt(), m = sc.nextInt();
  10.             int[] a = new int[m];
  11.             for (int i = 0; i < m; i++)
  12.                 a[i] = sc.nextInt();
  14.             int ans = 0;
  16.             for (int i = 2; i <= n; i++) {
  17.                 ans = (ans + a[(n - i) % m]) % i;
  18.             }
  19.             System.out.println(ans);
  20.         }
  22.     }
  23. }

参考：约瑟夫环——公式法（递推公式）

390. 消除游戏

列表 arr 由在范围 [1, n] 中的所有整数组成，并按严格递增排序。请你对 arr 应用下述算法：

  • 从左到右，删除第一个数字，然后每隔一个数字删除一个，直到到达列表末尾。
  • 重复上面的步骤，但这次是从右到左。也就是，删除最右侧的数字，然后剩下的数字每隔一个删除一个。
  • 不断重复这两步，从左到右和从右到左交替进行，直到只剩下一个数字。

给你整数 n ，返回 arr 最后剩下的数字。

示例 1：
输入：n = 9 输出：6 解释： arr = [1, 2, 3, 4, 5, 6, 7, 8, 9] arr = [2, 4, 6, 8] arr = [2, 6] arr = [6]
示例 2：
输入：n = 1 输出：1

提示：

  • 1 <= n <= 109

思路：
递归处理
记从左往右处理[1, n]，为函数f，剩余数为f(n)
记从右向左处理[n, 1]，为函数g，剩余数为g(n)
f(n)和g(n)最终的结果正好是对称的，即f(n) + g(n) = n + 1
又因为从左向右处理完后，剩余数字为2, 4, 6, 8, ...
数字个数为n / 2，将每个数除以2得1, 2, 3, ..., n / 2
故f(n) / 2 = g(n / 2)
最终能求得f(n) = 2 * (n / 2 + 1 - f(n / 2))

递归的终止条件为只剩1，返回1即可。

  1. class Solution {
  2.     public int lastRemaining(int n) {
  3.         if (n == 1) return 1;
  4.         return 2 * (n / 2 + 1 - lastRemaining(n / 2));
  5.     }
  6. }